$\color{red}物理之城退坛声明$

（标题是以前发的，改不了；附知识点“数字华容道的无解问题”）

我从2023/9/18注册论坛，到2024/7/2基本退坛，这288天是我在论坛的活跃时期。基本退坛主要是因为论坛太水和经常骂战。但基本退坛还不是完全退坛，而是偶尔会来论坛看一下，因为我认为我的帖子不够完美。直到2025/7/13，我终于完成了对所有帖子的修改，宣布在2025/7/14正式退坛！

在活跃时期，高三的我发了不少学术性帖子，在题目互答也帮助了很多人，使得自己在论坛有较高的地位，也使得高考运气好，考上了西湖大学，当然也发了几篇水帖。我还认识了很多大佬，详见本帖“物理之城的论坛大佬朋友圈”部分。

在基本退坛时期，虽然很少上论坛，但我还是见证了O-Box分区的出现，并完成了对帖子的修改，之前发的水帖不想删，就改。我的所有学术性帖子已经移至O-Box分区，每日一题都附上了答案，所有水帖都附上了知识点，所有帖子都达到了中高质量和35+赞藏，详见本帖“物理之城帖子总目录”部分。

从2025/7/14开始，我不会再上论坛了。我在论坛一共665天时间就这么结束了。你们可以顶我的帖子，只要用来顶帖的评论不太水就行，我的所有帖子允许有意义考古。你们还可以在这个群里找到我：（问我问题就算了，大学玩了一年，很多题都不会做了）

$\color{red}物理之城的论坛大佬朋友圈$

（2025/6/29更新）

注：

1.由于我在2023/9~2024/6期间活跃，此后基本退坛，本帖仅列出我在2023/9~2024/6期间在论坛认识的大佬

2.大佬的学术实力和论坛影响力是我主观确定的，仅供参考；而且是在2025/6/29确定的，不代表2023/9~2024/6期间的实力

3.因为有些人会改昵称，所以加上链接到个人主页。如果平板打不开个人主页的链接，可以通过代表帖进入个人主页

4.代表帖只是为了平板也能进入大佬的个人主页，多数是几年前的老帖，请勿随意考古。而且代表帖不一定是最好的帖子，大家不要特别在意

5.“核心区”和“外围区”的分类标准是我自己能否记住这些大佬

大佬！mol！

核心区：

@Nature 【物竞，学术实力S，论坛影响力S】（代表帖：常微分算符）

@Questioner 【生竞，学术实力S，论坛影响力S】（代表帖：竞赛中的争议问题（新））

@流光の宸 【论坛维护+化竞，学术实力S，论坛影响力S】（代表帖：新人水论坛必看(质心论坛生存守则））

@ref：rain 【物竞+论坛维护，学术实力S，论坛影响力S】（应大佬本人要求，不设代表帖）

@三等分的伊文斯 【物竞+论坛维护，学术实力S，论坛影响力S】（代表帖：第一届原神崩坏三理论物理考试试题）

@舟律 【物竞，学术实力S，论坛影响力A】（代表帖：关于浸渐不变量(感觉挺好用的，但没人提)）

@酥山 【物竞+数竞，学术实力A，论坛影响力A】（代表帖：随缘更新打卡贴）

@即未新用户8848114514 【物竞+数竞，学术实力A，论坛影响力A】（代表帖：数学区每日一题）

@一职的man 【物竞，学术实力A，论坛影响力A】（代表帖：一职的竞赛书评贴）

外围区：

@活性自由基 【化竞，学术实力S，论坛影响力A】（代表帖：论坛App端LaTeX的Bug处理手册）

  （小号：@不活性的自由基 ，代表帖：积分术法（Oλοκλήρωση Μαγεία）原典（卷一））

@稻 【物竞，学术实力S，论坛影响力A】（代表帖：K维理想气体麦克斯韦速率分布律）

@无名氏的木人 【生竞，学术实力S，论坛影响力A】（代表帖：某个废物致各位萌新）

@一个听AW的物竞牲 【物竞，学术实力S，论坛影响力B】（代表帖：电动力学导论（笔记整理））

  （旧号：@一个听AW的物竞牲 ，代表帖：物理竞赛题目分享（非原创））

@即未用户？？？  【数竞，学术实力A，论坛影响力A】（代表帖：还有没有数竞大佬，数学区人少，发物理）

@Yuki 【数竞，学术实力A，论坛影响力B】（代表帖：『YUKI的解析几何历险记』）

@蒟蒻凡姐 【物竞，学术实力A，论坛影响力B】（代表帖：行列式展开求助）

@导 【物竞，学术实力B，论坛影响力A】（代表帖：长风破浪会有时，直挂云帆济沧海）

@南虞 【物竞，学术实力B，论坛影响力B】（代表帖：来个小题目）

$\color{red}物理之城帖子总目录$

（按发帖日期排序；所有帖子均在物理区）

学术区（O-Box分区）：

7. 物理竞赛【每日一题】浏览大楼（附LaTeX常见符号汇总） （2024/1/12发帖，编号31275）

8. 【每日一题】Level 1 质点运动学 （2024/1/12发帖，编号31276）

9. 【每日一题】Level 2 静力学 （2024/1/26发帖，编号31765）

10. 2024九省联考数学原创解析 （2024/2/29发帖，编号32988）

11. 高中数学题目分享 （2024/3/13发帖，编号33402）

13. 【每日一题】Level 3 牛顿运动定律 （2024/5/1发帖，编号35280）

14. 用竞赛方法解高中物理易错题 （2024/6/20发帖，编号36812）

非学术区：

功能性帖子：

1. 物理竞赛小调查 （2023/9/23发帖，编号28189）（学习规划分区）（含：物理竞赛学习规划类问题汇总）

5. 质心月考题改编 （2023/12/16发帖，编号30507）（全部分区）（已改为：论坛钓鱼题汇总）

6. 论坛数据与建议 （2023/12/23发帖，编号30703）（划水摸鱼分区）（含：论坛违规类型汇总）

故事性帖子：

12. 《2024九省联考数学原创解析》背后的故事 （2024/3/21发帖，编号33776）（这有梦想分区）

混合性帖子（附知识点的水帖）：

2. 一个很有意思的小调查 （2023/9/29发帖，编号28377）（划水摸鱼分区）（已改为：退坛声明+大佬汇总+帖子总目录+数字华容道的无解问题）

3. 高三以来历次大考成绩汇总 （2023/10/21发帖，编号29122）（这有梦想分区）（含：高考志愿填报小知识）

4. 水帖专用帖（英语） （2023/11/4发帖，编号29432）（全部分区）（已改为：英语小知识汇总）

$\color{red}数字华容道的无解问题$

一、引入

数字华容道，也叫数字推盘游戏，英文名number klotski，也叫n-puzzle（对于m*m的数字华容道，$n=m^2−1$）。本文就以4*4数字华容道为例，如图

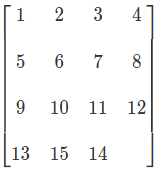
我以前了解到，如果把14和15换位置（如上图），就无解

然后我试了一下，最后一行如果只把13和14换位置，或者只把13和15换位置，也无解（会转化为14和15换位置的情况），而下图两种情况有解

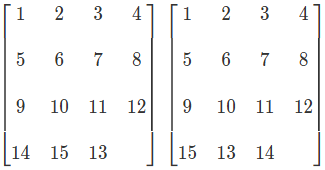
我还发现，如果在15个数字中交换任意两个数字的位置，无解，如果交换两次，有解，如果交换三次，又无解

当时的我想用编程做一个数字华容道，我希望电脑打乱出来的一定有解

所以我猜想：交换奇数次无解，交换偶数次有解

在电脑中，可以先随机打乱（保证空位在右下角），再判断交换几次可以恢复到初始状态（已经复原的状态），如果是奇数次，就再交换14和15

结果发现，每次用电脑打乱出来的都有解

说明我的猜想大概率是对的！但是不保证一定对，因为我当时还不会证明

下面我们就来证明这个猜想确实是对的

二、证明无解

求证：在4*4数字华容道初始状态下的15个数字中交换任意两个数字的位置，交换奇数次后一定无法正常复原（n*n的数字华容道同理）

证明：

（一）距离

定义空位与右下角的“距离”为空位与右下角格子的横坐标之差加上纵坐标之差

每次把与空位相邻的数字移到空位上，“距离”就+1或-1

复原前和复原后的“距离”都为0，所以移动的次数一定为偶数次

如果把空位视为数字16，那么一次移动也是一次交换，但是只能移动偶数次，所以只要证明移动偶数次一定不能复原，就证明了无解的情况

（二）行列式

我们用一个16*16的矩阵来表示4*4数字华容道中数字的位置

把空位视为数字16，数字华容道中第a个数字是b，那么矩阵的第a列只有第b行是1，其它是0，例如：

初始状态下，所有1都在主对角线（左上-右下对角线）上，行列式为1

那么上图16*16的矩阵的行列式怎么计算呢？

可以用递归法，首先，1*1矩阵的行列式就是矩阵中的数字

对于n*n的矩阵，从第一行选一列，用被选中的数字（第一行被选中的列的数字）乘以剩余矩阵（原矩阵去掉第一行和被选中的列）的行列式，如果选的是第偶数列，再乘以-1，最后把n种选择的结果相加

对于每一行每一列都恰好一个1的矩阵（排列矩阵），每次递归都只有一种非零的选择

如上图16*16的矩阵，选择第一列，如果去掉第一行第一列的剩余矩阵的行列式是$x$，那么整个矩阵的行列式也是$x$，再用同样的方法（递归法）求$x$的值，最后递归到1*1矩阵，行列式就算出来了

现在你算出上图16*16的矩阵的行列式了吗？是1还是-1？

行列式还有一个性质：交换矩阵的任意两列（或两行），行列式变为相反数

这个性质可以用递归法证明，2*2显然，然后假设n*n成立，证明(n+1)*(n+1)成立，具体就不证明了

而交换矩阵的任意两列，对应的是交换数字华容道的任意两个数字

初始状态下行列式为1，交换奇数次后，行列式为-1

把空位视为数字16，移动就是数字与空位的交换

如果移动奇数次，空位不可能在右下角，如果移动偶数次，行列式不可能为1，所以无论移动多少次，都不可能复原

证毕！

（三）逆序对

下面再用逆序对来证明一次。

数列$\{x_n\}$如果存在$\begin{cases}m\lt n\\x_m\gt x_n\end{cases}$，那么$(x_m,x_n)$就是一个逆序对

排列是一种特殊的数列，就是把数字1~n打乱顺序，n个数的排列最多有$\dfrac{n(n-1)}{2}$个逆序对

排列中第a个数字是b，对应的矩阵第a列只有第b行是1，其它是0，排列中的逆序对就是矩阵中有一个1在另一个1的左下方

容易证明，交换排列矩阵的任意两列，逆序对个数的变化是奇数

数字华容道就是一种排列，初始状态下没有逆序对，交换奇数次后，逆序对个数是奇数

把空位视为数字16，移动就是数字与空位的交换

如果移动奇数次，空位不可能在右下角，如果移动偶数次，逆序对个数仍然是奇数，所以无论移动多少次，都不可能复原

证毕！

（四）行列式与逆序对的联系

前面提到过，交换矩阵的任意两列（或两行），行列式变为相反数；交换排列矩阵的任意两列，逆序对个数的变化是奇数

其实行列式还有一种计算方法，就是提前把每一行要选哪一列想好，就不用递归了

对于n*n的矩阵，一共有 $n!=1\times2\times\cdots\times n$ 种选法，排列矩阵只有一种非零选法

比如上图第11行要选第12列，如果用递归法，第11行选的时候前10列已经被去掉了，剩下要选第2列，要乘以-1

那么如何判断第12列是剩下的第2列？

第11行12列的1的左下方还有一个1，那个1所在的列还没有被去掉

所以，如果一个排列有k个逆序对，那么对应的排列矩阵的行列式是$(-1)^k$，交换任意两列，行列式变为相反数

而对于一般的矩阵，行列式 $D=\sum\limits_{\{p_1,p_2,\cdots,p_{16}\}=\{1,2,\cdots,16\}}(-1)^ka_{1,p_1}^{}$    （求和符号枚举所有1~16的排列）

三、证明有解

求证：在4*4数字华容道初始状态下的15个数字中交换任意两个数字的位置，交换偶数次后一定可以正常复原（n*n的数字华容道同理）

证明：

证明数字华容道有解的过程，其实就是复原数字华容道的教程，如下图

根据下图，无论怎么打乱，你一定能复原到只剩11,12,15三个数字

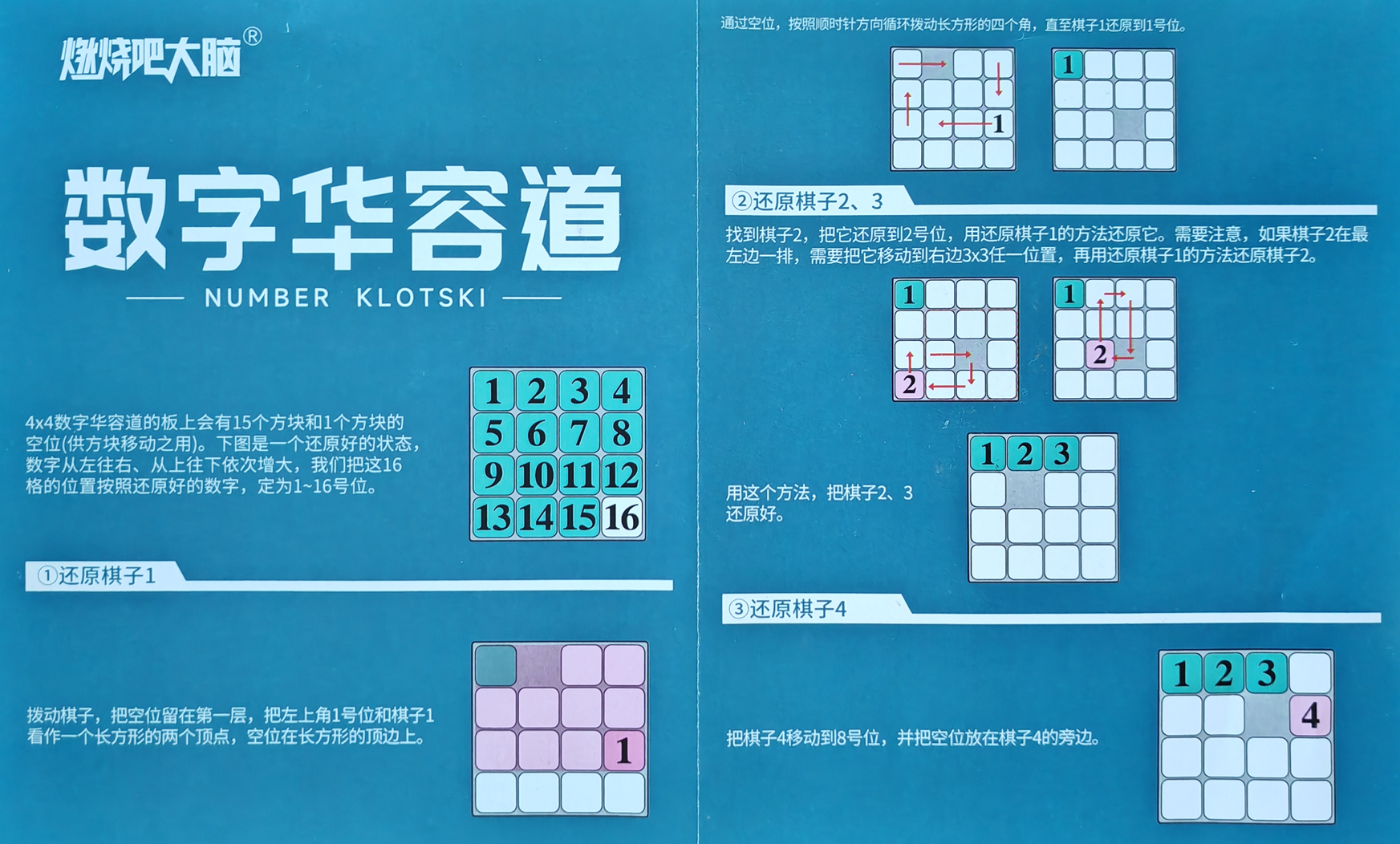
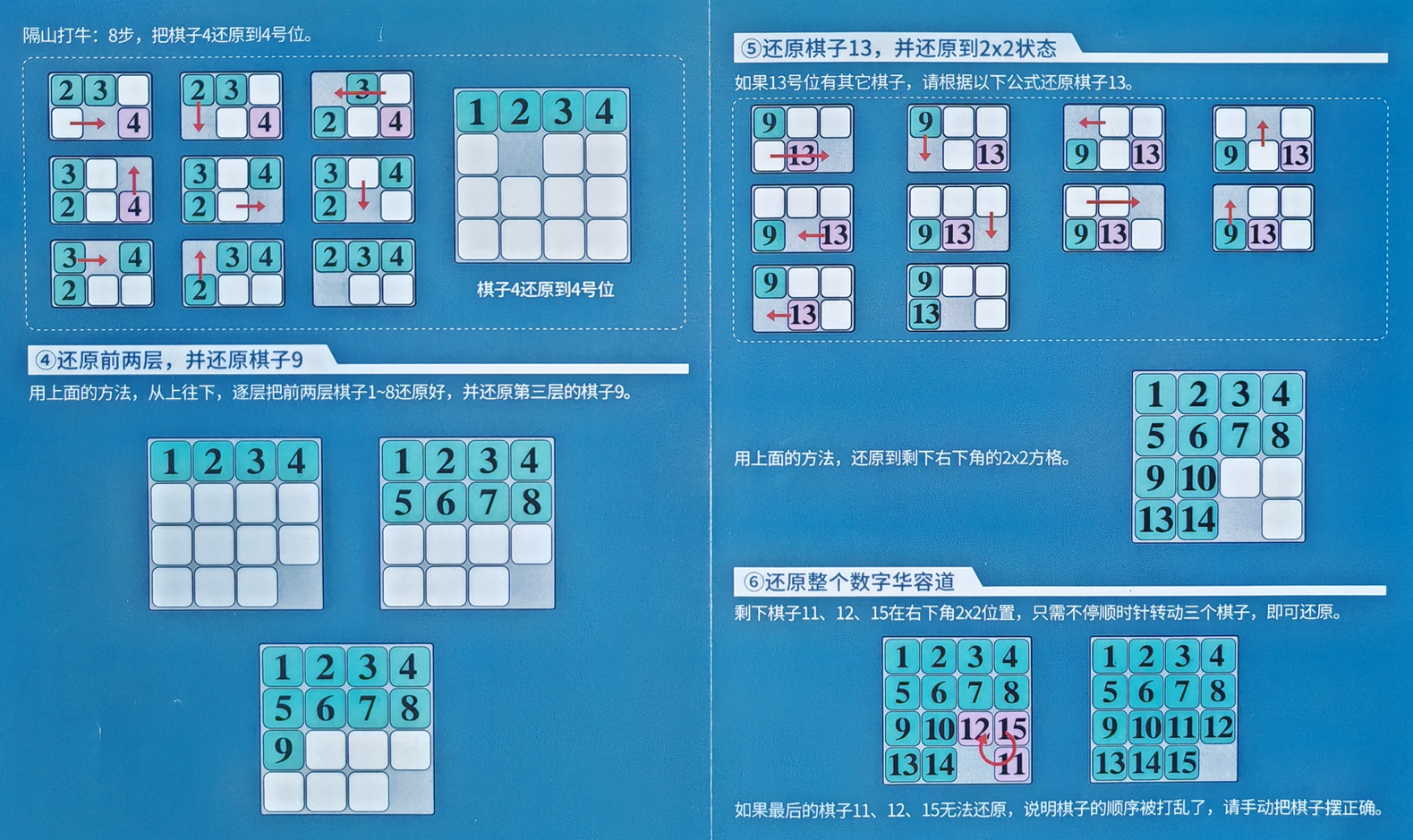
初始状态下行列式为1（没有逆序对），交换偶数次后，行列式为1（逆序对个数是偶数）

按上面的方法进行复原，只剩11,12,15三个数字没有复原且空位在右下角时，因为复原前和复原后的“距离”都为0，所以移动的次数一定为偶数次，行列式仍为1（逆序对个数是偶数）

虽然三个数字有6种排列，但是只有以下3种满足行列式为1（逆序对个数是偶数），这3种都可以复原（其中1种已经复原好）

（另外3种其实就是把初始状态中的两个数字交换了一次，是无解的）

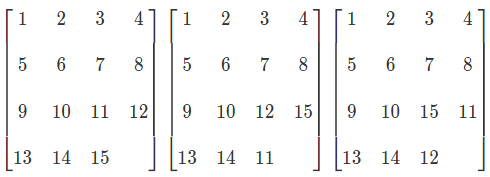
所以交换偶数次的一定可以正常复原

证毕！