（后面有“三角恒等变换公式”和“圆锥曲线相关结论”）

第一部分  坑题

例1  圆台

（金丽衢十二校联考）圆台的上、下底面半径分别为1、4，侧面积为10π，则母线长为________

注：以直角梯形垂直于底边的腰所在直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫做圆台．旋转轴叫做圆台的轴．直角梯形上、下底旋转所成的圆面称为圆台的上、下底面，另一腰旋转所成的曲面称为圆台的侧面，侧面上各个位置的直角梯形的腰称为圆台的母线，圆台的轴上的梯形的腰的长度叫做圆台的高，圆台的高也是上、下底面间的距离。圆台也可认为是圆锥被它的轴的两个垂直平面所截的部分，因此也可称为“截头圆锥”。

【答案】不存在

【解析】

错解：

圆台的侧面展开图为扇环，扇环的内、外半径之比为1：4，补成扇形之后（也就是把圆台补成圆锥），面积为$S'=\frac{16}{15}S=\frac{32π}{3}$

下底面周长为$l=8π$

根据扇形面积公式$S'=\frac{1}{2}lr'$，得$r'=\frac{8}{3}$，则圆台的母线长为$L=\frac{3}{4}r'=2$

正解1：

用错解的方法求得$L=2\lt3=R-r$，而圆台的母线长必须大于上、下底面半径之差，所以该圆台不存在

正解2：

若上、下底面重合，则侧面积为15π，所以圆台的侧面积大于15π，题目说是10π，所以该圆台不存在

【思考1】

如果考试时遇到这种题，你会把“不存在”写在答题纸上吗？

【练习1】

（5分）（这篇帖子）

例2  概率

（金丽衢十二校联考）从100件样品（其中70件合格品）中随机抽取2件，若其中一件为合格品，求另一件也为合格品的概率

【答案】$\dfrac{23}{43}$

【解析】

错解：

抽取一件为合格品，则剩下99件样品中有69件合格品，再抽取一件，为合格品的概率$\dfrac{69}{99}=\dfrac{23}{33}$

正解：

记事件A为抽到一件合格品，事件B为抽到两件合格品

$P(AB)=\dfrac{C_{70}^2}{C_{100}^2}=\dfrac{\frac{70\times69}{2}}{\frac{100\times99}{2}}$

$P(A)=1-\dfrac{C_{30}^2}{C_{100}^2}=\dfrac{\frac{100\times99}{2}-\frac{30\times29}{2}}{\frac{100\times99}{2}}$

$P(B|A)=\dfrac{P(AB)}{P(A)}=\dfrac{70\times69}{100\times99-30\times29}=\dfrac{23}{43}$

【思考2】

这道题的题目表述有没有问题？

【练习2】

（12分）（Z20联盟）

第二部分  解析几何

例3  硬解定理

直线$Ax+By+C=0$与椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$交于$(x_1,y_1),(x_2,y_2)$两点，求$x_1+x_2,x_1x_2,|x_1-x_2|,x_1y_2+x_2y_1,|x_1y_2-x_2y_1|$

【解析】

通分，得$b^2B^2x^2+a^2B^2y^2=a^2b^2B^2$

代入直线，得$b^2B^2x^2+a^2(Ax+C)^2=a^2b^2B^2$

$(a^2A^2+b^2B^2)x^2+2a^2ACx+a^2C^2-a^2b^2B^2=0$

韦达定理，得

$x_1+x_2=\dfrac{-2a^2AC}{a^2A^2+b^2B^2}$

$x_1x_2=\dfrac{a^2C^2-a^2b^2B^2}{a^2A^2+b^2B^2}$

$|x_1-x_2|=\sqrt{(x_1+x_2)^2-4x_1x_2}=\dfrac{\sqrt{4a^2b^2B^2(a^2A^2+b^2B^2-C^2)}}{|a^2A^2+b^2B^2|}$

$x_1y_2+x_2y_1=x_1(-\dfrac{Ax_2+C}{B})+x_2(-\dfrac{Ax_1+C}{B})=\dfrac{2a^2b^2AB}{a^2A^2+b^2B^2}$

$|x_1y_2-x_2y_1|=|x_1(-\dfrac{Ax_2+C}{B})-x_2(-\dfrac{Ax_1+C}{B})|=\dfrac{\sqrt{4a^2b^2C^2(a^2A^2+b^2B^2-C^2)}}{|a^2A^2+b^2B^2|}$

验算：（算出来相当于A,B互换，a,b互换）

$y_1+y_2=-\dfrac{Ax_1+C}{B}-\dfrac{Ax_2+C}{B}=\dfrac{-2b^2BC}{a^2A^2+b^2B^2}$

$y_1y_2=(-\dfrac{Ax_1+C}{B})(-\dfrac{Ax_2+C}{B})=\dfrac{b^2C^2-a^2b^2A^2}{a^2A^2+b^2B^2}$

$|y_1-y_2|=\dfrac{A}{B}|x_1-x_2|=\dfrac{\sqrt{4a^2b^2A^2(a^2A^2+b^2B^2-C^2)}}{|a^2A^2+b^2B^2|}$

【思考3】

如何将上述结论推广到双曲线？

【练习3】

（12分）

例4  抛物线的二级结论

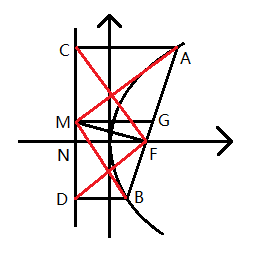
（多选）已知抛物线$E:y^2=2px$  (p>0)，O为坐标原点，直线$l$过焦点$F(\dfrac{p}{2},0)$，倾斜角为$θ$，交$E$于$A(x_1,y_1),B(x_2,y_2)$，过A,B分别作准线的垂线，垂足分别为C,D，AB中点为G，CD中点为M，准线交x轴于N

A. $|AF|=x_1+\dfrac{p}{2}=\dfrac{p}{1-\cos\theta}$，$|AB|=x_1+x_2+p=\dfrac{2p}{\sin^2\theta}$，$y_1y_2=-p^2$，$x_1x_2=\dfrac{p^2}{4}$

B. CF平分∠AFN，∠CFD=90°，AM平分∠FAC，FN平分∠ANB，∠AOB为钝角

C. 以AB为直径的圆与准线相切于M，以AF为直径的圆与y轴相切，以CD为直径的圆与AB相切于F

D. A,O,D三点共线，AM与抛物线相切，AM与CF的交点在y轴上

【答案】ABCD

【解析】

A项：正确

根据抛物线的定义，$|AF|=|AC|=x_1+\dfrac{p}{2}$

$\theta\in(0,\dfrac{\pi}{2})$时，作$FH\perp AC$于$H$，则$|HC|=|FN|=p$，$\cos\theta=\dfrac{|AH|}{|AF|}=\dfrac{|AF|-p}{|AF|}$

得$|AF|=\dfrac{p}{1-\cos\theta}$  （$\theta\in(\dfrac{\pi}{2},\pi)$同理，$\theta=\dfrac{\pi}{2}$显然成立）

同理，$|BF|=x_2+\dfrac{p}{2}=\dfrac{p}{1+\cos\theta}$

$|AB|=|AF|+|BF|=x_1+x_2+p=\dfrac{2p}{\sin^2\theta}$

设$l:x=ty+\dfrac{p}{2}$，代入抛物线得$y^2-2pty-p^2=0$，韦达定理，得$y_1y_2=-p^2$，$x_1x_2=\dfrac{y_1^2}{2p}\dfrac{y_2^2}{2p}=\dfrac{p^2}{4}$

B项：正确

∵|AC|=|AF|，AC//NF，∴∠AFC=∠ACF=∠CFN，∴CF平分∠AFN

同理，DF平分∠BFN，$∠CFD=∠CFN+∠DFN=\frac{1}{2}(∠AFN+∠BFN)=90°$

∴在Rt△CFD中，M为CD中点，|CM|=|MF|

∴$△ACM\cong△AFM$  (SSS)，∴∠CAM=∠FAM，∴AM平分∠FAC

平行线截得的线段长成比例，$|NC|:|FA|=|ND|:|FB|$，∴$|NC|:|AC|=|ND|:|BD|$，∴$\tan∠ANC=\tan∠BND$，∴$∠ANF=∠BNF$，∴FN平分∠ANB

$\overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=-\dfrac{3p^2}{4}\lt0$，∴∠AOB为钝角

C项：正确

GM是梯形ACDB的中位线，$|GM|=\frac{1}{2}(|AC|+|BD|)=\frac{1}{2}(|AF|+|BF|)=\frac{1}{2}|AB|=|AG|$

∴M在以AB为直径的圆上，又∵GM垂直准线，∴以AB为直径的圆与准线相切于M

设AC交y轴于C'，梯形AC'OF的中位线$|G'M'|=\frac{1}{2}(|AC'|+|OF|)=\frac{1}{2}(|AC'|+|CC'|)=\frac{1}{2}|AC|=\frac{1}{2}|AF|$

∴M'在以AB为直径的圆上，又∵G'M'垂直y轴，∴以AF为直径的圆与y轴相切

∵$△ACM\cong△AFM$，∴|CM|=|MF|，∠ACM=∠AFM=90°，∴F在以CD为直径的圆上，MF⊥AB，∴以CD为直径的圆与AB相切于F

D项：正确

∵|MC|=|MF|，|AC|=|AF|，∴AM⊥CF，又∵CF⊥DF，∴AM//DF，∴∠CMA=∠NDF

又∵|CD|=2|CM|，|NF|=2|ON|，∴tan∠CDA=tan∠NDO，∴A,O,D三点共线

设AC交y轴于C'，∴AD斜率倒数为$\dfrac{x_1}{y_1}=\tan∠C'OA=\tan∠CDA$

$x=\dfrac{y^2}{2p}$，$x'=\dfrac{y}{p}=\dfrac{2x}{y}$，∴过A的切线斜率倒数为$\dfrac{2x_1}{y_1}=2\tan∠CDA=\tan∠CMA$，∴AM与抛物线相切

设AM交y轴于P，则$2\tan∠C'OA=\tan∠CMA=\tan∠C'PA$，∴P为OC'中点

∵|CC'|=|OF|，CC'//OF，∴AM与y轴交点为OC'中点，∴AM与CF的交点在y轴上

【思考4】

如果直线$l$不过焦点，上述结论还成立吗？抛物线还有哪些二级结论？

【练习4】

（6分）（多选）

例5  面积转化

（九省联考第18题）

【答案】(1)定点(3,0)    (2) 8

【解析】

官方答案：

原创解析：详见2024九省联考数学原创解析

【思考5】

除了官方答案和原创解析给出的方法，还有什么方法可以将$S_{△GMN}$转化为$S_{四边形ADMN}$？

【练习5】

（17分）

第三部分  难题

例6  等差数阵

（三湘联考）如图，等差数阵的每一行、每一列都是等差数列，则2023在等差数阵中出现了________次。

【答案】6

【解析】

错解：

把每一行、每一列都写到2023或大于2023为止，根本不可能在2个小时之内写完

正解1：

等差数阵是对称的，所以只要算前32行，32行以后的一定在前32列

把前2列算到32行，得到每一行的首项和公差，判断（2023-首项）是否能被公差整除

能被公差整除的有3行（且都不在前32列），则前32列也有3列，所以2023出现了6次

大约要算20分钟，还是太浪费时间了

正解2：

写出前2行的通项公式$\begin{cases}a_{1,m}=7+3m\\a_{2,m}=8+5m\end{cases}$，相减得1+2m，从而得到等差数阵的通项公式$a_{n,m}=6+n+m+2nm$

令$a_{n,m}=2023$，得$(2n+1)(2m+1)=4035=3×5×269$

$(2n+1)(2m+1)=3×1345=5×807=15×269=269×15=807×5=1345×3$

所以2023出现了6次

【思考6】

等差数阵能扩展到3维甚至是n维吗？

【练习6】

（5分）若将其中一个13改为14，再求2023出现的次数

例7  函数最值

已知函数$f(x)=\dfrac{(x-1)(2x+1)(x^2+ax+b)}{x^2}$，对任意非零实数x，均满足$f(x)=f(-\dfrac{1}{x})$，则$f(x)$的最小值为________

【答案】$-\dfrac{9}{8}$​

【解析】

方法一：

$f(x)=\dfrac{(x-1)(2x+1)(x^2+ax+b)}{x^2}=\dfrac{2x^4+(2a-1)x^3+(2b-a-1)x^2+(-a-b)x-b}{x^2}$

$f(-\dfrac{1}{x})=\dfrac{(-1-x)(-2+x)(1-ax+bx^2)}{x^2}=\dfrac{-bx^4+(b+a)x^3+(2b-a-1)x^2+(1-2a)x+2}{x^2}$

$\begin{cases}2=-b\\2a-1=a+b\end{cases}$    $\Rightarrow\begin{cases}a=-1\\b=-2\end{cases}$

$f(x)=2x^2-3x-4+\dfrac{3}{x}+\dfrac{2}{x^2}$

$f'(x)=4x-3-\dfrac{3}{x^2}-\dfrac{4}{x^3}=0$

$4x^4-3x^3-3x-4=0$

因为$f(x)=f(-\dfrac{1}{x})$，所以方程$4x^4-3x^3-3x-4=0$的解$x_1,x_2$满足$x_1=-\dfrac{1}{x_2}$，即$x_1x_2=-1$

根据四次方程韦达定理，得$x_1x_2x_3x_4=-1$，即$x_3x_4=1$，不满足$x_3x_4=-1$

所以$x_3,x_4$满足$x=-\dfrac{1}{x}$，即$x^2+1=0$，解得$x=\pm\mathrm{i}$

所以$4x^4-3x^3-3x-4=[4(x-x_1)(x-x_2)][(x-x_3)(x-x_4)]=(4x^2+kx-4)(x^2+1)=4x^4+kx^3+kx-4$，解得$k=-3$

所以$4x^2-3x-4=0$，代入$f(x)=2x^2-3x-4+\dfrac{3}{x}+\dfrac{2}{x^2}$

$f(x)=(\dfrac{3}{2}x+2)-3x-4+\dfrac{3}{x}+\dfrac{2x^2-\frac{3}{2}x}{x^2}=-\dfrac{3}{2}x+\dfrac{3}{2x}=-\dfrac{3}{2}x+\dfrac{3x^2-\frac{9}{4}x}{2x}=-\dfrac{9}{8}$

方法二：

由原式得$f(1)=f(-\dfrac{1}{2})=0$，则$f(-1)=f(2)=0$，所以$x^2+ax+b=(x+1)(x-2)$

$f(x)=\dfrac{(x-1)(2x+1)(x+1)(x-2)}{x^2}$ （经检验，$f(x)=f(-\dfrac{1}{x})$）

$f(x)$在$(-1,-\dfrac{1}{2})$或$(1,2)$取相同的最小值，考虑$(1,2)$

$f(x)=-\dfrac{(x-1)(2x+1)(x+1)(2-x)}{x^2}=-\dfrac{(2x^2-2)(-2x^2+3x+2)}{2x^2}\ge-\dfrac{[(2x^2-2)+(-2x^2+3x+2)]^2}{8x^2}=-\dfrac{9}{8}$

【思考7】

把$4x^4-3x^3-3x-4=0$改为$4x^4+3x^3-3x-4=0$，这个方程又会有什么性质呢？

【练习7】

（8分）把$f(x)=f(-\dfrac{1}{x})$改为$f(x)=-f(\dfrac{1}{x})$，求$f(x)$的极大值和极小值

例8  离散对数

（九省联考第19题）

【答案】(1) 1    (2)(3)见解析

【解析】

官方答案：

【思考8】

如何完整地证明费马小定理（$a^{p-1}≡1~(\mathrm{mod}~p)$）？ （原题只证明了一种特殊情况）

【练习8】

（5分）求斐波那契数列$(a_1=a_2=1,a_n=a_{n-1}+a_{n-2})$的第n项除以5的余数

附1  三角恒等变换公式

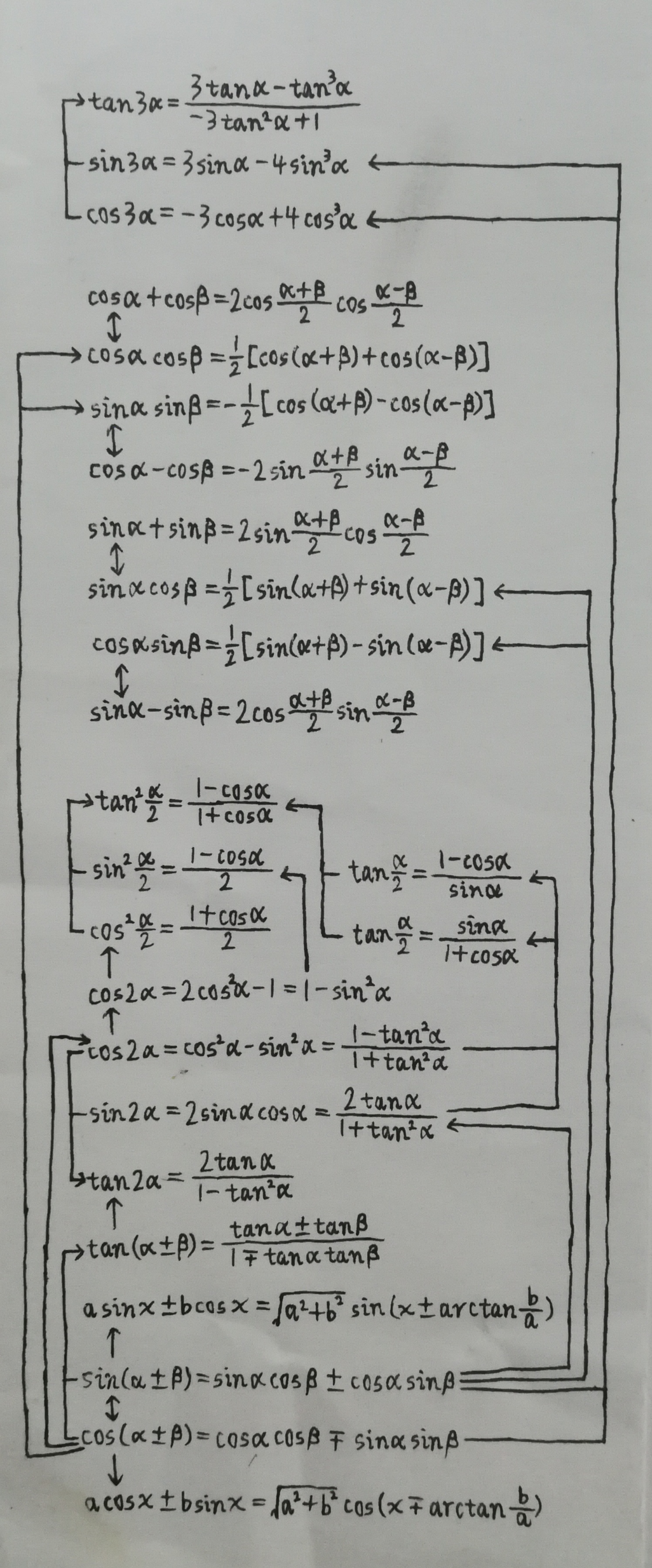
附2  圆锥曲线相关结论