物理

2024九省联考数学原创解析

第一部分：原卷呈现                                                                       

第二部分：官方答案                                                                      

第三部分：原创解析                                                                      

一、单选题

1.【答案】B

【解析】一共有9个数，从小到大排序，第5个数就是这组数据的中位数。那么要怎么排序呢？先找出最小的数10，划掉，再从剩下的数中找出最小的数12，划掉，再是两个14，划掉。还剩5个数，最小的就是中位数，是16。

2.【答案】A

【解析】这种题千万别算太快，老老实实列方程求解。

$\begin{cases}a^2=b^2+c^2\\b^2=1\\\frac ca=\frac12\end{cases}$

解得$a^2=\frac43,a=\frac{2\sqrt3}3$

3.【答案】C

【解析】方法一：$a_n$是等差数列，设通项公式$a_n=a_1+(n-1)d$，代入已知条件

$\begin{cases}2a_1+8d=6\\a_1+11d=17\end{cases}$

解得$a_1=-5,d=2$，代入前n项和公式$S_n=na_1+\frac{n(n-1)}2d$，得$S_{16}=160$

方法二：利用等差数列的性质$a_m+a_n=a_p+a_q~(m+n=p+q)$，得$a_3+a_7=2a_5=6,a_5=3$，得到公差$d=\dfrac{a_{12}-a_5}{12-5}=2$，进而推得$a_8=9,a_9=11$，再次使用这一性质，得前16项和$S_{16}=(a_1+a_{16})+(a_2+a_{15})+...+(a_8+a_9)=8(a_8+a_9)=160$

4.【答案】C

【解析】这种题建议用排除法，排除3个错的，剩下的就是对的。这道题的3个错误选项的反例都很好举。

A.若m,l都平行α与β的交线，则$m//l$

B.同样设m,l都平行α与β的交线，不同的是m,l都在平面内，则$m//l$时，α与β相交

C.这个是正确选项。证明：

设m上有一点P，$l$与P确定一个平面，记为γ，再设$α∩γ=m_1,β∩γ=m_2$，根据线面平行的性质，得$l//m_1,l//m_2$，又因为$m_1,m_2$有公共点P，所以$m_1$与$m_2$重合，即$m_1=m_2=m$，所以$m//l$

D.垂直于同一直线的所有平面平行，垂直于平行直线的所有平面也平行，不是垂直（题目说α与β是两个平面，所以一般不考虑重合，但也不排除某些题目表述不严谨，要考虑重合的可能）

5.【答案】B

【解析】乙和丙隔2个，只能是乙1丙4、乙2丙5、乙4丙1、乙5丙2这4种，它们都是乙和丙占了一端，另一端不能是甲，所以剩余3个位置有2个是甲可以选的，还剩2个位置2个人，有2种情况。根据乘法原理，不同排法共有4*2*2=16种

6.【答案】C

【解析】Q的轨迹$l$是一条直线，且对于任意一点Q，都能根据QP向量确定唯一一点P，所以P的轨迹可以由Q的轨迹沿QP向量平移得到，根据直线平移的性质，P的轨迹E是一条与$l$平行的直线，排除ABD，选C。下面证明C是对的：

方法一：取$l$上特殊点$Q(-1,0)$，得$P(0,-3)$，根据点到直线的距离公式$d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$，得P到$l$的距离$d=\dfrac{|2\times(-3)+1|}{\sqrt{1^2+2^2}}=\sqrt5$

方法二：$l$的斜率是$-\frac12$，QP的斜率是-3，根据两角和差的正切公式，得$l$与QP的夹角为45°（数感好的人能记住$\arctan\frac12+\arctan\frac13=\fracπ4$，可以不用算直接得出这一结论），又$|QP|=\sqrt{10}$，得P到$l$的距离为$\sqrt5$

7.【答案】A

【解析】方法一：把所有角度化为θ，然后齐次化求解

$\tan2θ=\dfrac{2\tanθ}{1-\tan^2θ}=-4\times\dfrac{1+\tanθ}{1-\tanθ}=-4\tan(θ+\fracπ4)$

$\dfrac{2\tanθ}{1+\tanθ}=-4(1+\tanθ)$

$2\tan^2θ+5\tanθ+2=0$

$\tanθ=-2(舍去)或-\frac12$

$原式=\dfrac{\sin^2θ+\cos^2θ+2\sinθ\cosθ}{2\cos^2θ+2\sinθ\cosθ}=\dfrac{\tan^2θ+1+2\tanθ}{2+2\tanθ}=\dfrac{1}{4}$

方法二：观察到$2θ=2(θ+\frac{π}{4})-\frac{π}{2},\tan2(θ+\frac{π}{4})=-\dfrac{1}{\tan2θ}$，左式可化为

$\tan2(θ+\frac{π}{4})=\dfrac{2\tan(θ+\frac{π}{4})}{1-\tan^2(θ+\frac{π}{4})}=\dfrac{1}{4\tan(θ+\frac{π}{4})}$

$\tan(θ+\fracπ4)=-\frac13(舍去)或\frac13$，注意$(θ+\fracπ4)$的范围是$(π,\frac{5π}4)$

代入左式，得$\tan2θ=-\frac43$

注意$2θ$的范围是$(\frac{3π}2,2π),\sin2θ=-\frac45,\cos2θ=\frac35$

$原式=\dfrac{1+\sin2θ}{\cos2θ+1+\sin2θ}=\dfrac14$

8.【答案】D

【解析】过原点的直线与双曲线的交点关于原点对称，所以$F_1,A,F_2,B$构成平行四边形，根据双曲线的定义，邻边之差为2a，所以长边为4a，短边为2a，再根据数量积为$4a^2$，得夹角为60°，所以$AF_1$与$AF_2$的夹角为120°，在$△AF_1F_2$中，根据余弦定理，得$F_1F_2=2\sqrt7a=2c,e=\frac ca=\sqrt7$

二、多选题

9.【答案】AC

【解析】$f(x)=\sin x+\cos x$应该是你比较熟悉的函数，它可以化为$f(x)=\sqrt2\sin(x+\frac{π}{4})$

所以这道题用换元法，设$t=2x+\frac{3π}{4},f(x)=g(t)=\sqrt2\sin(t+\frac{π}{4})$

显然最小值为$-\sqrt2$，D错误

选项A、B都与对称轴有关，$y=\sin x$的对称轴为$x=kπ+\frac{π}{2}$，令$t+\frac{π}{4}=kπ+\frac{π}{2}$，得$t=kπ+\frac{π}{4}$，再代入$t=2x+\frac{3π}{4}$，得$x=\frac{kπ}{2}-\frac{π}{4}$，B错误

多选题，排除B、D两个选项后，就可以选AC了

$f(x-\frac{π}{4})$的对称轴为$x-\frac{π}{4}=\frac{kπ}{2}-\frac{π}{4}$，即$x=\frac{kπ}{2}$，$x=0$是它的一条对称轴，根据偶函数与对称轴的关系（偶函数是$f(-x)=f(x)$），A正确

$x∈(\frac{π}{3},\frac{π}{2})$代入t，得$t∈(\frac{17π}{12},\frac{7π}{4}),t+\fracπ4∈(\frac{5π}{3},2π)$，相当于$y=\sin x$在$(\frac{5π}3,2π)$，即$(-\fracπ3,0)$上单调递增，C正确

10.【答案】BCD

【解析】$z^2$可能是虚数，$|z|^2$一定是实数，A错误（注意复数与向量的区别）

上下同乘z（实数的运算规律，复数都可以用），得$\dfrac z{\bar z}=\dfrac{z^2}{z\bar z}=\dfrac{z^2}{|z|^2}$，B正确，其中用到了一个常用结论$z\bar z=|z|^2$，虽然用复数的代数形式可以证明，但还是要把结论记住，尤其是平方不能漏

C是共轭复数的性质，C正确（把减改成加、乘、除也正确），可以用复数的代数形式证明，这里只证明选项中的：

$\overline{z-w}=\overline{(a+b{\rm i})-(c+d{\rm i})}=\overline{(a-c)+(b-d){\rm i}}$ $=(a-c)-(b-d){\rm i}={(a-b{\rm i})-(c-d{\rm i})}=\bar z-\bar w$

D是共轭复数的性质，D正确（把除改成乘、乘方也正确），用复数的代数形式证明比较麻烦，可以直接记结论，也可以用复数的三角形式证明：

$|\frac{z}{w}|=|\frac{|z|(\cosα+{\rm i}\sinα)}{|w|(\cosβ+{\rm i}\sinβ)}|=|\frac{|z|}{|w|}[\cos(α-β)+{\rm i}\sin(α-β)]|=\frac{|z|}{|w|}|\cos(α-β)+{\rm i}\sin(α-β)|=\frac{|z|}{|w|}$

11.【答案】ABD

【解析】方法一：这种题的一般方法是把x,y的特殊值代入函数方程中，一般先考虑0,1,题给数字等特殊值，这里先考虑0

令y=0，得$f(x)+f(x)f(0)=f(x)\cdot(1+f(0))=0$，若$f(x)=0$，则与$f(\frac12)≠0$矛盾，所以$f(0)=-1$

得出这一结论后，就不能再令x,y=0了，又要用到$f(0)=-1$，所以令$x=-y=\frac12$，得$f(0)+f(\frac12)f(-\frac12)=-1$，即$f(\frac12)f(-\frac12)=0$，又$f(\frac12)≠0$，所以$f(-\frac12)=0$，A正确

令$y=-\frac12$，得$f(x-\frac12)+0=-2x$，满足$f(-x+\frac12)=-f(x-\frac12)$，是奇函数，不是偶函数，C错误

$f(x-\frac12)=-2x=-2(x-\frac12)-1$，即$f(x)=-2x-1$，$f(\frac12)=-2$，B正确

$f(x+\frac12)=-2(x+\frac12)-1=-2x-2$，是减函数，D正确

因为在解函数方程的过程中，解是唯一的，所以如果时间紧，可以不用检验（除非题目出错了，比如高中数学题目分享的例1），但如果出现多解，就一定要检验。

检验：$f(x+y)+f(x)f(y)=-2(x+y)-1+(-2x-1)(-2y-1)=-2(x+y)-1+4xy+2(x+y)+1=4xy$，所以$f(x)=-2x-1$符合原式

方法二：标准解法

三、填空题

12.【答案】5

【解析】设a是A中的一个元素，则$a∈A∩B$，又$a∈A$，所以$a∈B$，对任意a都成立，所以$A⊆B$

$|x-3|≤m$等价于$-m≤x-3≤m$，即$3-m≤x≤3+m$

对任意a都满足这个范围，得$3-m≤-2\lt4≤3+m$，解得$m≥5$

13.【答案】$\dfrac23$，  1

【解析】这题首先要审清题目，圆锥的高与球的直径相等，可以列出等式$h=2R$，再根据圆锥的轴截面为正三角形，得$h=\sqrt3r,l=2r,R=\frac{\sqrt3}2r$

圆锥和球的体积和表面积公式一定要记住，体积比$\frac13(πr^2)h:\frac43πR^3=\frac{\sqrt3}3πr^3:\frac{\sqrt3}2π r^3={}2:3$，表面积比$(πrl+πr^2):4πR^2={}3πr^2:3πr^2={}1:1$

14.【答案】$\dfrac15$

【解析】$\max\{b-a,c-b,1-c\}$的几何意义是数轴上a到b的距离、b到c的距离、c到1的距离的最大值，要让这个最大值最小，首先a越大越好，所以题中的不等式要取等号；其次c必须是b和1的中点，此时$\max\{c-b,1-c\}=\frac{1-b}2$

题中的不等式有“或”的关系，先考虑$b≥2a$，取等号，$b=2a$，即$b-a=a=\frac b2$，所以$\max\{b-a,c-b,1-c\}=\max\{\frac b2,\frac{1-b}2\}≥\frac14$，当且仅当$b=\frac12$时取等

再考虑$a+b≤1$，取等号，$a+b=1$，即$b-a=1-2a=2b-1$，所以$\max\{b-a,c-b,1-c\}=\max\{2b-1,\frac{1-b}2\}$，画出$y=2b-1$和$y=\frac{1-b}2$的图像，交点$(\frac35,\frac15)$，所以$\max\{2b-1,\frac{1-b}2\}≥\frac15$，当且仅当$b=\frac35$时取等

由于两个条件只需满足一个，第二个条件可以取更小的值，所以最小值为$\frac15$

四、解答题

15.【答案】(1) -3    (2)见解析

【解析】

(1)

$2x+3y=0$    $⇒y=-\frac23x,k_1=-\frac23$

垂直，$k_1k_2=-1$    $⇒k_2=\frac32=f'(2)$

$f'(x)=\frac1x+2x+a$

$f'(2)=\frac92+a=\frac32$    $⇒a=-3$

(2)

$f'(x)=\frac1x+2x-3$  $(x\gt0)$

$f'(x)=0$    $⇒2x^2-3x+1=0$

解得$x_1=\frac12,x_2=1$

列表：（列表比直接描述更好，但不能有了列表就不下结论）

递增区间$(0,\frac12),(1,+\infty)$，递减区间$(\frac12,1)$

$x=\frac12$时，$f(x)$有极大值$\frac34-\ln2$；$x=1$时，$f(x)$有极小值0

16.【答案】(1) $\dfrac47$    (2)见解析；$\dfrac{10}7$

【解析】

(1)

设A=“取出的3个小球上的数字两两不同”

方法一：$P(A)=\dfrac{C_4^3(C_2^1)^3}{C_8^3}=\dfrac{4×2^3}{56}=\dfrac47$（先选3种数字，再每种数字选一个小球）

方法二：$P(\bar A)=\dfrac{C_4^1C_6^1}{C_8^3}=\dfrac{4×6}{56}=\dfrac37$（从反面考虑，先选1种数字的两个小球，再从剩下的选一个小球）

$P(A)=1-P(\bar A)=\dfrac47$

(2)

X的可能值为1,2,3

方法一：$P(X=1)=\dfrac{C_2^1C_6^2+C_2^2C_6^1}{C_8^3}=\dfrac9{14}$（数字1选1或2个小球，后面选2或1个小球）

$P(X=2)=\dfrac{C_2^1C_4^2+C_2^2C_4^1}{C_8^3}=\dfrac27$（数字2选1或2个小球，后面选2或1个小球）

$P(X=3)=\dfrac{C_2^1C_2^2+C_2^2C_2^1}{C_8^3}=\dfrac1{14}$（数字3选1或2个小球，后面选2或1个小球）

方法二：$P(X=3)=\dfrac{C_4^3}{C_8^3}=\dfrac1{14}$（X=3时，只能从后4个小球里选）

$P(X≥2)=\dfrac{C_6^3}{C_8^3}=\dfrac5{14}$（X≥2时，只能从后6个小球里选）

$P(X=1)=1-P(X≥2)=\dfrac9{14}$

$P(X=2)=P(X≥2)-P(X=3)=\dfrac27$

列表：（这个一定要列，否则可能会扣分）

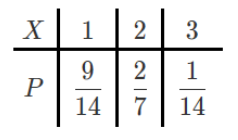
数学期望$E(X)=1×\dfrac9{14}+2×\dfrac27+3×\dfrac1{14}=\dfrac{10}7$

17.【答案】(1)见解析    (2)$\dfrac{2\sqrt2}3$

【解析】

（(1)要证明的垂直是(2)建系的基础，所以(1)用几何法，(2)用建系法）

(1)

连结$C_1B,C_1D$

在正方形ABCD中，$CB=CD=\sqrt2OC=\sqrt2OB=\sqrt2OD=2$

在平行六面体中，$CC_1=AA_1=2$（把自己要用到的由“正方形”和“平行六面体”得出的条件放在前面，方法与答案不同的时候不容易失分）

方法一：（全等）

$∵CB=CD,∠C_1CB=∠C_1CD,C_1C=C_1C$

$∴△C_1CB≅△C_1CD$

$∴C_1B=C_1D$

方法二：（余弦定理）

$∵CB=CD,∠C_1CB=∠C_1CD$

$∴C_1B=\sqrt{C_1C^2+CB^2-2C_1C⋅CB\cos∠C_1CB}=\sqrt{C_1C^2+CD^2-2C_1C{}⋅C{}D\cos∠C_1CD}=C_1D$

又$∵OB=OD$

$∴$在$△C_1BD$中，$C_1O⊥BD$

$∵C_1C=\sqrt2OC,∠C_1CO=45°$

$∴OC=C_1C\cos∠C_1CO$

$∴$在$△C_1CO$中，$C_1O⊥OC$

又$∵OC∩BD=O$

$∴C_1O⊥$平面$ABCD$

(2)

在正方形ABCD中，$AC⊥BD$（有了垂直才能建系）

如图，建立空间直角坐标系

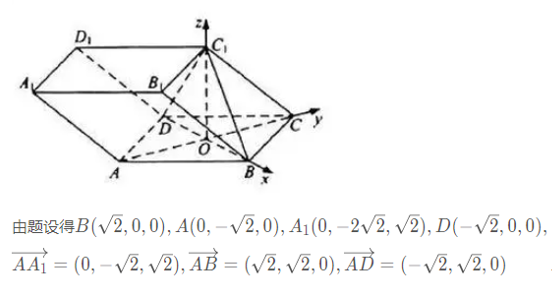
设平面$AA_1B$的法向量为$\vec{n_1}=(x,y,z)$

方法一：$\begin{cases}\vec{n_1}⋅\overrightarrow{AA_1}=-\sqrt2y+\sqrt2z=0\\\vec{n_1}⋅\overrightarrow{AB}=\sqrt2x+\sqrt2y=0\end{cases}$

得$x=-y=-z$，令$x=-1$，得$\vec{n_1}=(-1,1,1)$

方法二：（向量的叉乘）  $(x_1,y_1,z_1)×(x_2,y_2,z_2)=(y_1z_2-z_1y_2,z_1x_2-x_1z_2,x_1y_2-y_1x_2)$

$\overrightarrow{AA_1}×\overrightarrow{AB}=(-2,2,2)=2\vec{n_1}$，得$\vec{n_1}=(-1,1,1)$

根据对称性，平面$AA_1D$的法向量$\vec{n_2}=(1,1,1)$  （关于yOz平面对称，x分量改变符号）

设二面角$B-AA_1-D$的大小为θ，$θ∈[0,π]$

$|\cosθ|=\dfrac{|\vec{n_1}⋅\vec{n_2}|}{|\vec{n_1}||\vec{n_2}|}=\dfrac1{\sqrt3×\sqrt3}=\dfrac13$  （$\cosθ$和$\vec{n_1}⋅\vec{n_2}$都要加绝对值，因为二面角是锐角还是钝角与法向量点乘的正负无关）

$\sinθ=\sqrt{1-\cos^2θ}=\dfrac{2\sqrt2}3$  （最后一步不能漏）

18.【答案】(1)定点(3,0)    (2) 8

【解析】

(1)

第一步：设（共14个未知数）

设$A(x_1,y_1),B(x_2,y_2),E(x_3,y_3),D(x_4,y_4),M(x_5,y_5),N(x_6,y_6),l_{AB}:x=k_1y+1,l_{DE}:x=k_2y+1~(k_1,k_2≠0)$

（不建议设成$A(\dfrac{y_1^2}4,y_1)$，否则不容易得步骤分）

第二步：列（共13个方程）

（$A,B,E,D$在直线和抛物线上，8个方程，这里不列出）

（中点，4个方程）$2x_5=x_1+x_2,2y_5=y_1+y_2,2x_6=x_3+x_4,2y_6=y_3+y_4$

（垂直，1个方程）$k_1k_2=-1$

（$l_{AB}$代入抛物线，韦达定理简化计算，不算方程个数）$y^2-4k_1y-4=0$

$y_1+y_2=4k,y_1y_2=-4$

第三步：析

定点问题，未知数比方程多1个，可解

用韦达定理算出M的坐标，用同构法（就是直接替换字母下标）得出N的坐标，再找$x_5,y_5,x_6,y_6$的关系

第四步：解

$x_5=\dfrac{x_1+x_2}2=\dfrac{y_1^2+y_2^2}8=\dfrac{(y_1+y_2)^2-2y_1y_2}8=1+2k_1^2$

$y_5=\dfrac{y_1+y_2}2=2k_1$

$x_6=1+2k_2^2=1+\dfrac2{k_1^2}$

$y_6=2k_2=-\dfrac2{k_1}$

$k_{MN}=\dfrac{y_5-y_6}{x_5-x_6}=\dfrac{2k_1^3+2k_1}{2k_1^4-2}=\dfrac{k_1(k_1^2+1)}{(k_1^2+1)(k_1^2-1)}=\dfrac{k_1}{k_1^2-1}$

$l_{MN}:y-y_5=k_{MN}(x-x_5)$

$x=\dfrac{k_1^2-1}{k_1}y+3$

过定点(3,0)  （关于x轴对称，定点一定在x轴上；可以先用特殊情况找定点，再证明）

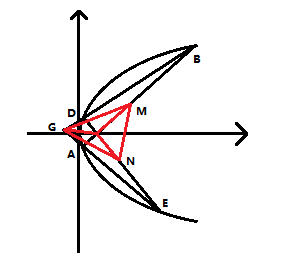
(2)

方法一：

第一步：设（共17个未知数）

除(1)外，再设$G(x_7,y_7),S_{△GMN}=S$  （最值问题，要把需要求最值的变量设出来）

第二步：列（共16个方程）

除(1)中的13个方程，还有：

（G为交点，2个方程）$\dfrac{y_7-y_1}{x_7-x_1}=\dfrac{y_7-y_3}{x_7-x_3},\dfrac{y_7-y_2}{x_7-x_2}=\dfrac{y_7-y_4}{x_7-x_4}$

（三角形面积公式，1个方程）$S=|(x_5-x_7)(y_6-y_7)-(x_6-x_7)(y_5-y_7)|$

第三步：析

最值问题，未知数比方程多1个，可解

先算出G的坐标，再用$k_1$表示S，最后求最值

第四步：解（太难算了，过程略，可以算出$x_7=-1$）

方法二：

G的坐标和三角形面积都很难算，考虑将三角形拆分为多个三角形，再转化

连结GF，$S_{△GMN}=S_{△FMN}+S_{△FGM}+S_{△FGN}$

利用“M,N是中点”的性质，得$S_{△FGM}=S_{△AGM}-S_{△AGF}=\frac12S_{△AGB}-S_{△AGF}=\frac12(S_{△FGB}-S_{△AGF})$

同理，$S_{△FGN}=\frac12(S_{△FGE}-S_{△DGF})$

$S_{△GMN}=S_{△FMN}+\frac12[(S_{△FGB}-S_{△DGF})+(S_{△FGE}-S_{△AGF})]=S_{△FMN}+\frac12(S_{△FBD}+S_{△FAE})$

此时已经不需要算G的坐标了，求$S_{△GMN}$转化成了求3个直角三角形的面积，比方法一好算多了（计算过程略）

方法三：

继续转化，$S_{△FBD}=S_{△FDM}+S_{△DBM}=S_{△FDM}+S_{△DAM}=S_{△FAD}+2S_{△FDM}$

同理，$S_{△FAE}=S_{△FAD}+2S_{△FAN}$

所以$S_{△GMN}=S_{四边形ADMN}$  （比方法二更好算了）

$y^2-4k_1y-4=0$，$|y_2-y_1|=\dfrac{\sqrtΔ​}{a}=4\sqrt{1+k_1^2}$

$|AB|=\sqrt{1+k_1^2}|y_2-y_1|=4(1+k_1^2)$  （注意$k_1$是斜率的倒数，右边是y不是x）

同理，$|DE|=4(1+k_2^2)$

$S=\frac12|AM||DN|=\frac18|AB||DE|=2(1+k_1^2)(1+k_2^2)$

（求最值）方法一：（柯西不等式）

不妨设$k_1\gt0,k_2\lt0$

$S=2(1+k_1^2)(1+(-k_2)^2)≥2×(1+k_1×(-k_2))^2=8$

当且仅当$k_1=-k_2=1$时取等

方法二：（对$k_1^2$求导）

$S=2(1+k_1^2)(1+\dfrac1{k_1^2})$

$S'=2[(1+\dfrac1{k_1^2})-\dfrac1{k_1^4}(1+k_1^2)]=0$

$k_1^2=1或-1(舍去)$

所以$k_1=1$时，S有最小值8

19.【答案】(1) 1    (2)(3)见解析

【解析】

（由于我没学过数学竞赛，我只能对官方答案做一些补充说明）

(1)简单

(2)设出n和m，原式可化为$a^{n,⊗}⊗a^{m,⊗}=a^{n⊕m,⊗}$，只需证$a^{n,⊗}⊗a^{m,⊗}=a^{n+m,⊗}$和$a^{p-1,⊗}=1$

前者需要设一些额外的整数，这已经很难想到了

后者即费马小定理，需要用反证法，设出同余，再相减得到整除，更难想到

(3)用到了⊗的交换律和结合律，严格来说这些也要证明，但这样题目就太复杂了

所以，这道题确实很难

第四部分：调查反馈