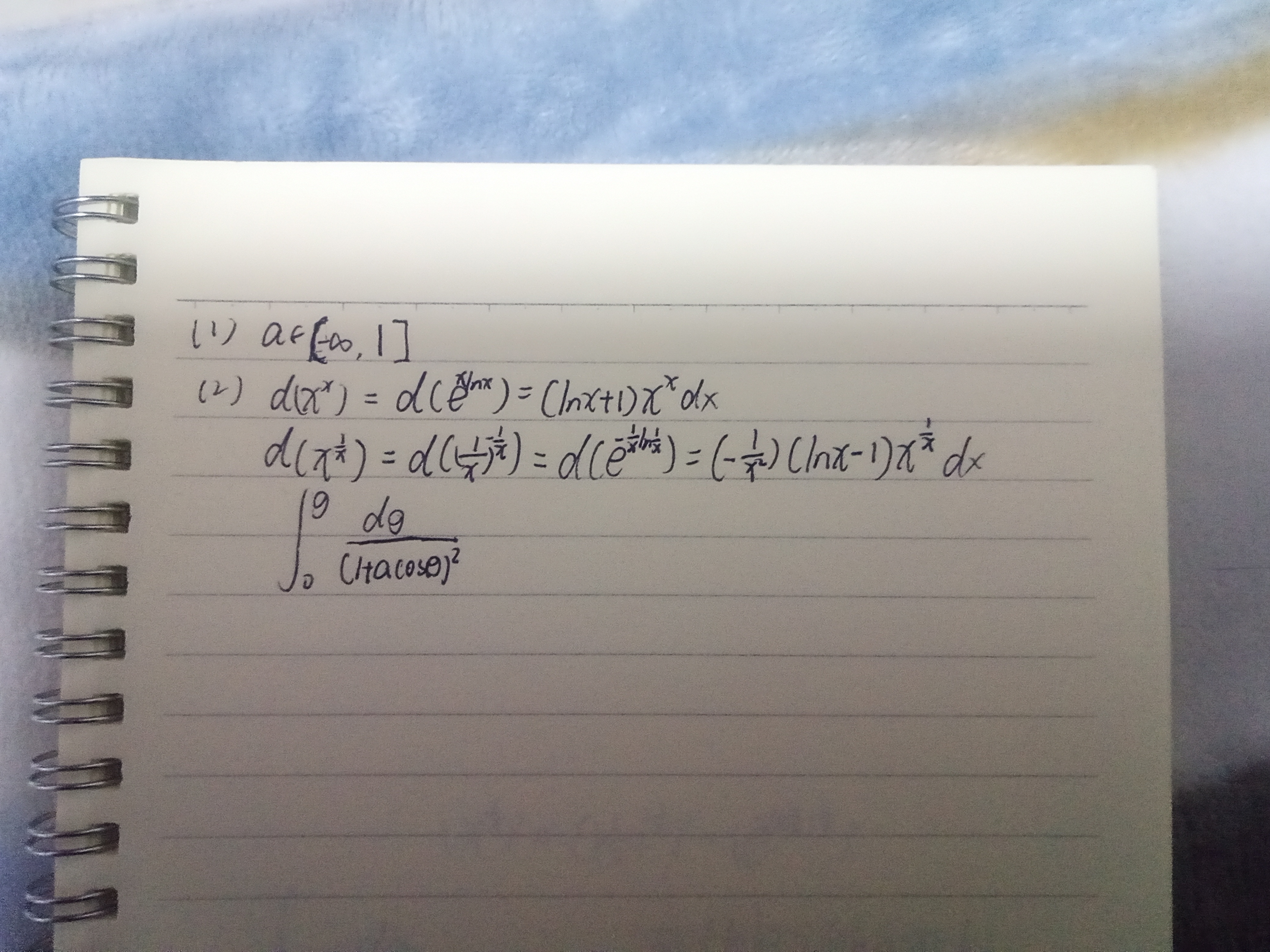物理 质心月考题改编
$\color{red}论坛钓鱼题汇总$
一、质心月考题改编
（改编题，由@物理之城 改编，原题为论坛经典题，质心出题）
（2023/12/16发的，当时很多人看到就说我大佬，说自己不会，最后直到2023/12/31发答案（答案在评论区），只有2个人做）
题目：
$\begin{cases}罗\le3a+2\\罗\gt4a+0.999999......\end{cases}$
（提示：数列极限的ε-N证明）
$\dfrac{\mathrm{d}(\sqrt[x]{x})}{\mathrm{d}(x^x)}周=\int_0^θ\dfrac{\mathrm{d}θ}{(1+a\cosθ)^2}$
（a>0且满足(1)中的取值范围，x>0，0≤θ<π/2）
二、这是什么钓鱼题？
（论坛经典题，由@质心哥哥 出题）
（原帖曾经在题目互答，导致评论区水积分严重，直到2024/6/28才移出题目互答；当时的我支持删除原帖，所以复制了一份到本帖，才有了现在的“论坛钓鱼题汇总”）
大家好啊，质心哥哥又来了
这个年底临近考试，大家都复习的怎么样了呢？
不知道大家有没有遇到过这种看起来很简单，甚至初学者能看懂的题，做起来却难道大佬的题目呢
比如下面这道
大家一起来分享一下遇到的类似题目吧
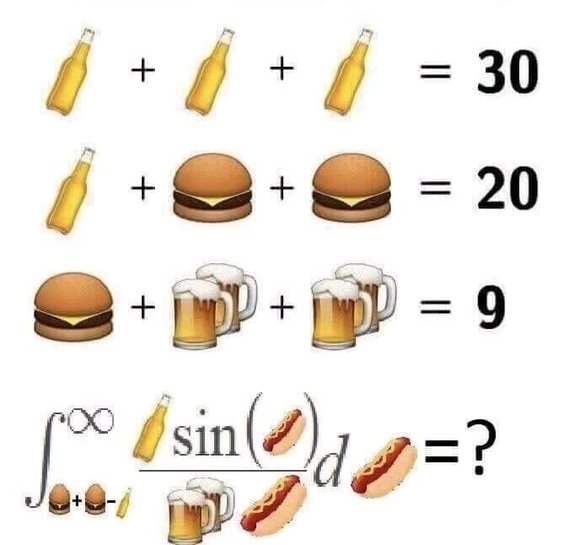
三、一年级的钓鱼题
（由@三等分的伊文斯 在论坛上提出）
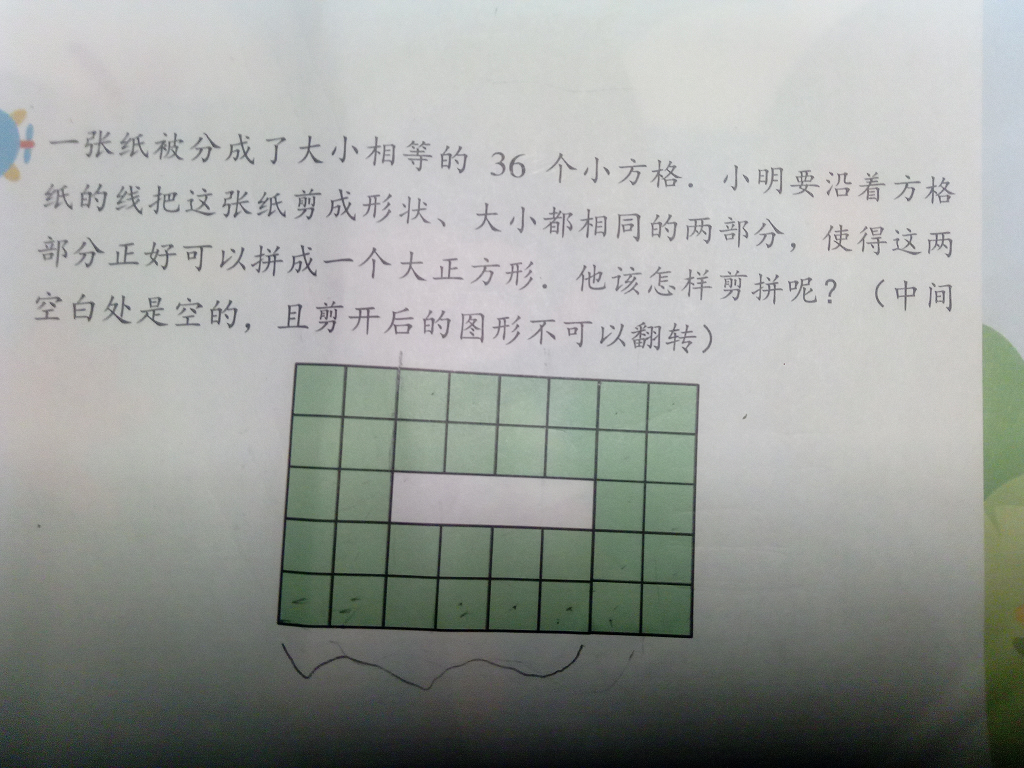
四、初中几何题
注意：解答题，要求用初中方法求解
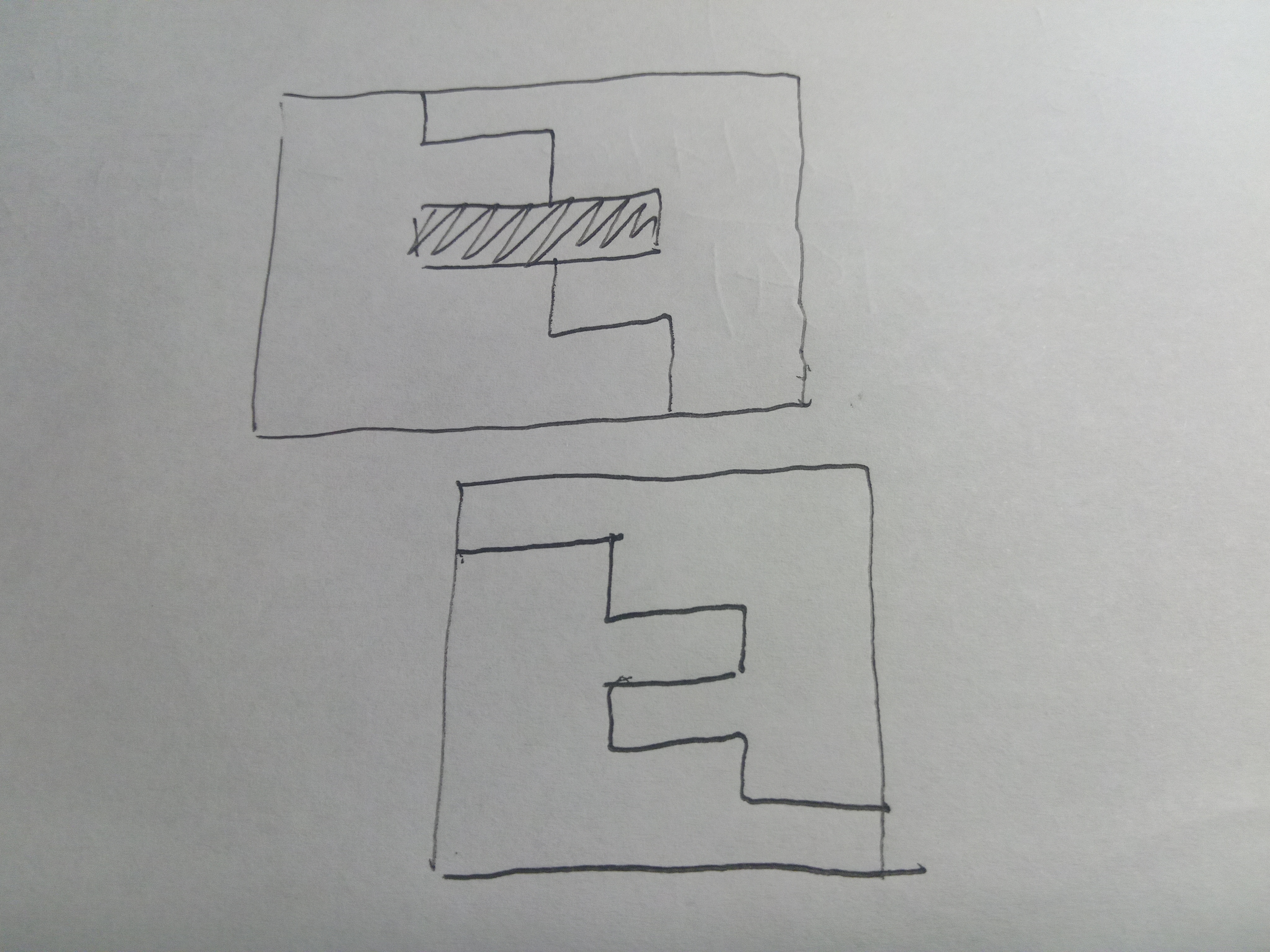
（一）
（由@Mistake. 在论坛上提出）
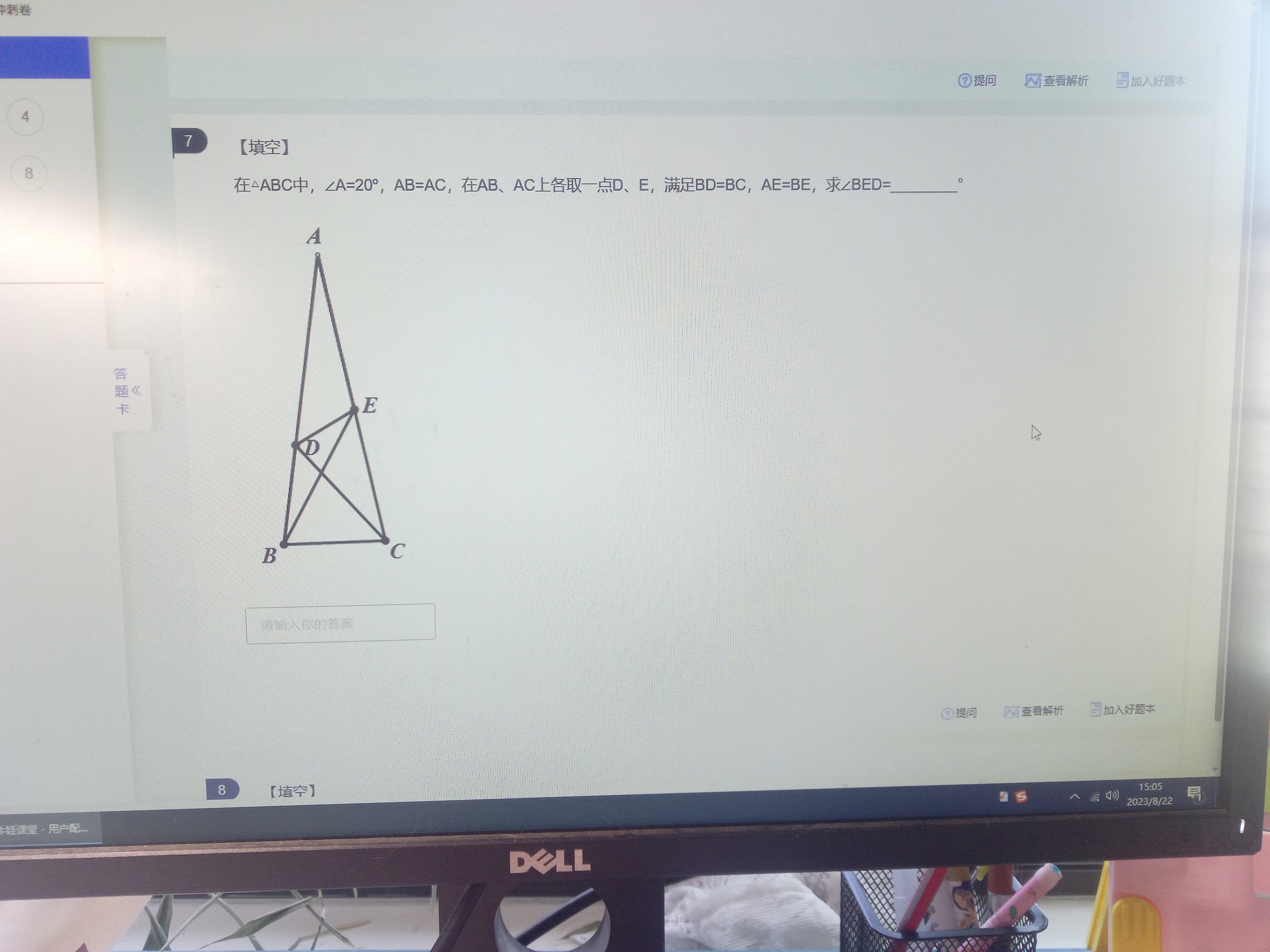
（二）
（由@自然哲学的救赎(邓布利多校长↝) 在论坛上提出）
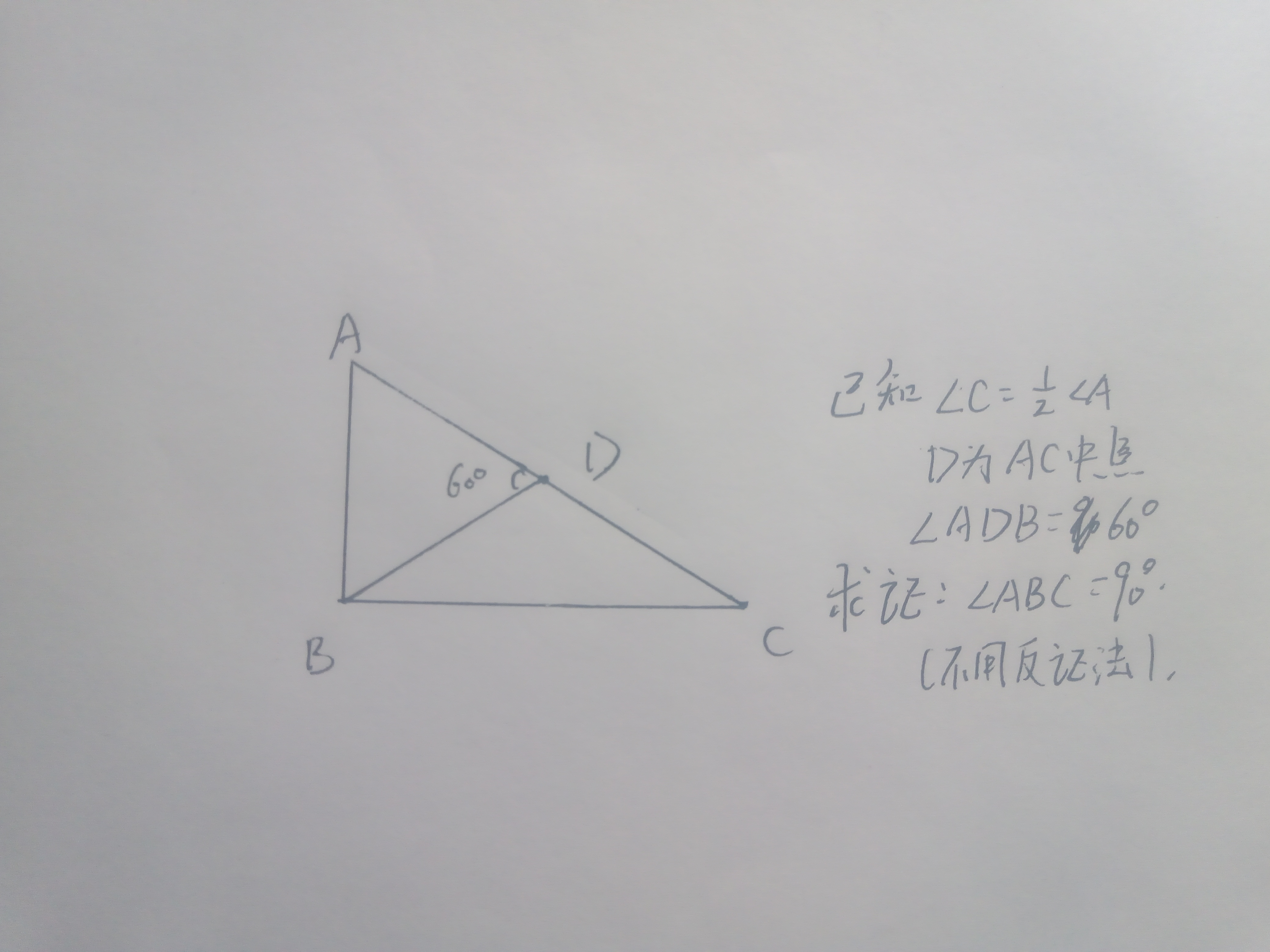
（三）
（由@种小蘑菇的锦叶OvO 在论坛上提出）
求2PD＋PC的最小值，注意A,P,C不一定共线，条件在图片里
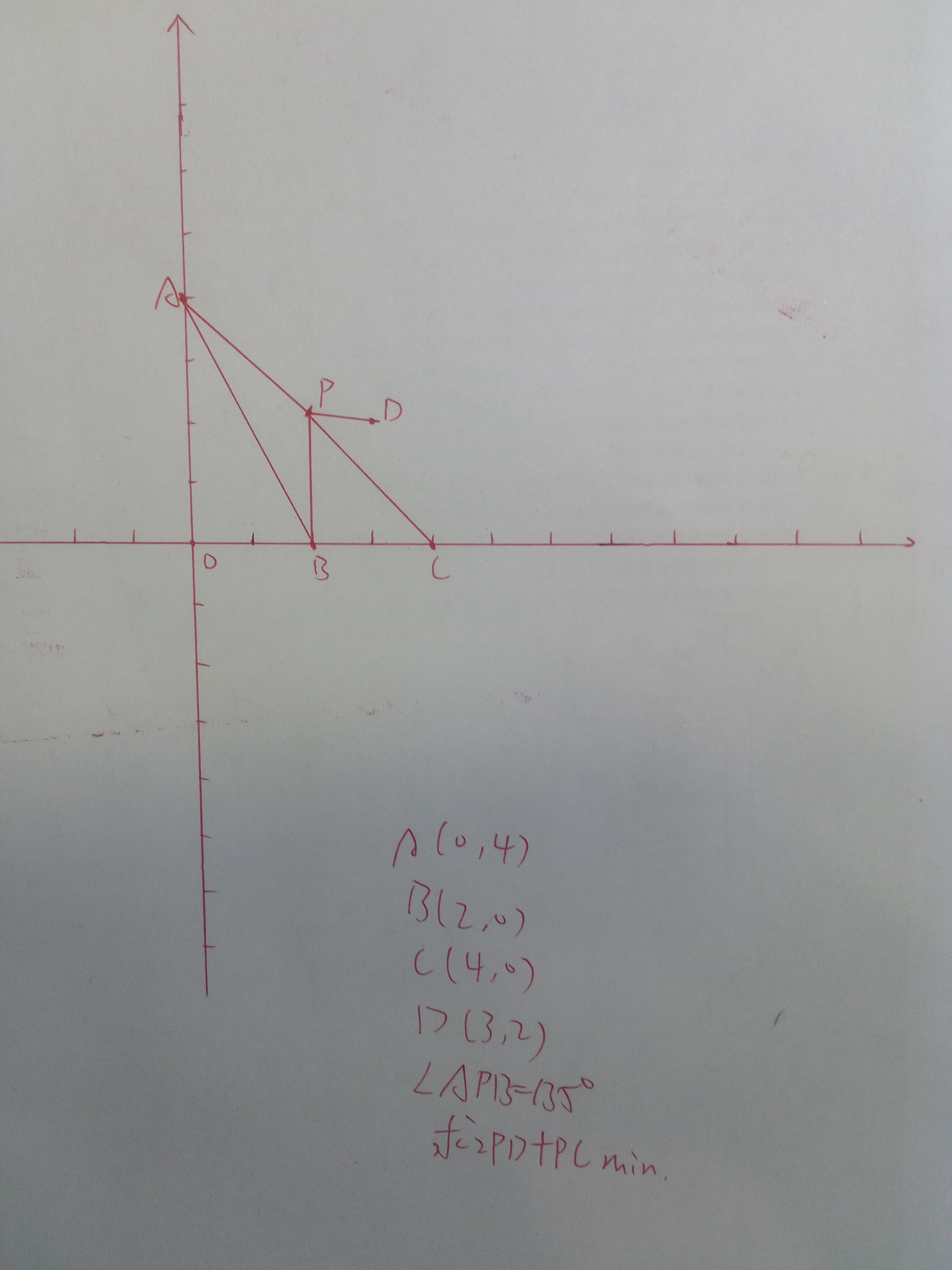
五、极限比大小
注意：不能使用计算器！
（1~13为高考难度题）
14.
（由@质心8888同学 在论坛上提出）
比较大小并证明：$a=\pi^3$ $b=3^\pi$ $c=31$
15.
（由@light. 在论坛上提出）
比较大小并证明：$a=(\dfrac{6}{5})^{\sqrt3}$ $b=(\dfrac{5}{4})^{\sqrt2}$
六、一个有意思的数学证明
（经典题，由@小粉兔 在论坛上提出）
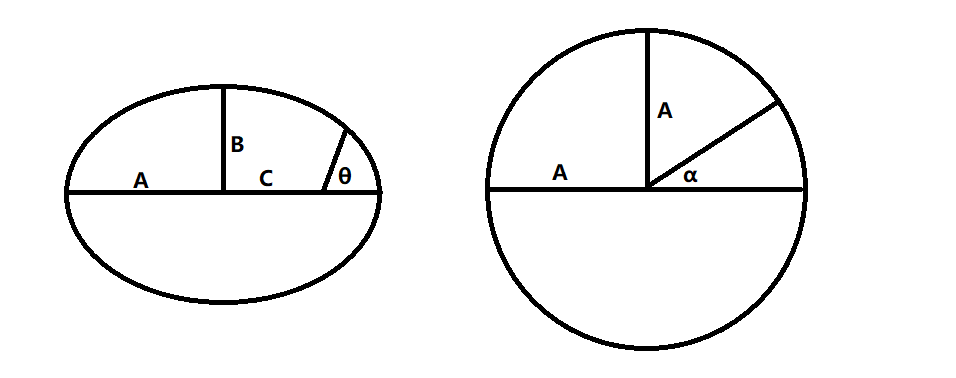
题就是说：有一个单位圆，圆上有n个点把圆周长n等分，然后随便选一个点，把这个点和其他(n-1)个点连起来，求证这些连线长度的乘积等于n。
一个粗略的图：
七、一个简单的网格染色问题
（经典题，由@σ-MiGration 在论坛上提出）
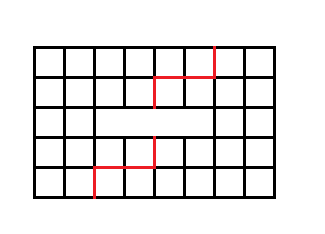
n*n的网格中，选取部分点染色，要求在网格中横向竖向以及两条对角线方向上，均不存在连续3个点都被染色。
求：n趋近于无限时，染色点的个数S的最大值与n²的比值。
要是把3改成m，答案又是多少？
八、找规律填数
（由@猫猫(/∇＼*) 在论坛上提出）
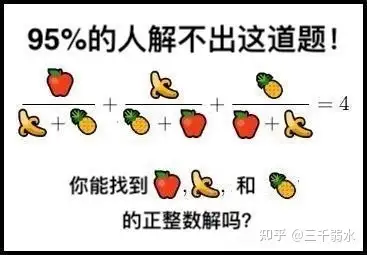
九、正整数解
（经典题，由@Rosemary 在论坛上提出）
十、小球栓在弹簧上
（质心出题，由@三等分的伊文斯 在论坛上提出）
注意：求“速度”需要求大小和方向，求大小很简单，用能量守恒，求方向就是钓鱼题（题目画的好像是水平方向，实际上不一定）
十一、一道功率题
（经典题，由@古城先生 在论坛上提出）
已知一起重机最大功率为P(不限最大拉力大小)，竖直拉起一重为m的物体（重力加速度为g），求位移−时间函数
十二、立体几何问题
（经典题，2024三地市二模）
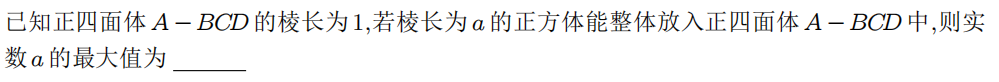
如果把正四面体、正方体、正八面体、正十二面体、正二十面体中的一个放入另一个，答案又是多少？
十三、取值个数问题
（经典题，由@接地的均匀Yuki 在论坛上提出）
就以下两种情况求$a^2+b^2$的取值个数：
(1)a,b为自然数，且$a,b\le n$ (2)a,b为正整数，且$a,b\le n$
十四、函数的连续性
（a~d为西湖大学出题；e为经典题）
（注：若$\lim\limits_{x\to a}f(x)=f(a)$，则f(x)在x=a处连续；若f(x)在(a,b)上的任意一点连续，则f(x)在(a,b)上连续。）
判断哪些命题是正确的：
a. 如果f(x)在(a,b)上连续，且f(a)<0，f(b)>0，则存在c∈(a,b)，使得f(c)=0
b. 如果f(x)在x=a处连续，且f(a)>0，则存在$δ$>0，使得当x∈(a-$δ$，a+$δ$)时f(x)>0
c. 如果一个函数在x=a处是连续且递增的，（即 f'(a)>0），则存在一个范围(a-$δ$，a+$δ$)，$δ$>0，函数在该范围内递增
d. 如果一个函数在x=a处连续，那么这个函数必定在一个包含a的微小区间上连续
e. 如果f(x)在(a,b)上连续且可导，那么f'(x)在(a,b)上连续
e. If f(x) is continuous and differentiable on (a,b), then f'(x) is continuous on (a,b).
更多钓鱼题，详见“这是什么钓鱼题？”专题标签
附：几个有趣的数学结论
（注：(1)(2)的链接源于网络（也就是指向论坛以外的链接），平板是打不开的，请用网页版打开）
(1)巴塞尔问题：$\sum\limits_{n=1}^∞\dfrac{1}{n^2}=\dfrac{π^2}{6}$
(2)全体正整数和为$-\dfrac{1}{12}$？及其物理意义
(3)自然数集是自然数吗？ @Nature （评论区有“1+1=2的形式证明”）
- 1
这道改编题不是新手轮的题，但是新手轮也能拿一部分分数
新手轮只会做把0.9循环看作1之后的第一问吧
我tm新手轮都不是
这个巴塞尔莫非是傅立叶初步？
，太可怕了不敢学。。。。
(1)没有过程，得0分（解答题一定要写过程！！！）
(2)得4分（积分算不来可以先放一放，先把算出来的代进去，注意读题）
“附”下面的只是科普，不用学
不会过程呢。。。话说这是数学题啊，我就不凑热闹了。。。
就是将原式一步步化简然后求出结果的过程，还有一个证明的过程
(1)得4分（证明过程对了，只差一步用0.999999......代$\lim\limits_{n\to\infty}x_n$，但是后面错了，第二个式子是大于）
但0.9循环不是趋近于1吗，只要大于等于1就行了
0.9循环比任何一个小于1的数都要大，所以它就是1
看来你还没有理解ε-N证明
还有，把原式先化简几步再代入0.9循环，分数就不会这么低了，送分最多的还是化简的过程
明白了，感谢大佬指正
答案公布！（其实我是想让不同层次的人都能得一些分数，结果。。。）
(1)
$4a+0.999999......<罗≤3a+2$ （2分）
$4a+0.999999......<3a+2$ （4分）
$a+0.999999......<2$ （6分）
$a<2-0.999999......$ （8分）
$∵0.999999......=1$ （9分）
$∴a<1$ （10分）
下面证明$0.999999......=1$
$0.999999......=\lim\limits_{n\to\infty}(1-\frac{1}{10^n})$ （11分）
$\frac{1}{10^n}≥0⇒\lim\limits_{n\to\infty}\frac{1}{10^n}≥0$ （12分）
$∀ε>0,∃N>\lg\frac{1}{ε},\frac{1}{10^N}<ε$ （13分）
$∀ε>0,\lim\limits_{n\to\infty}\frac{1}{10^n}<ε$ （14分）
$∴\lim\limits_{n\to\infty}\frac{1}{10^n}=0,即0.999999......=1$ （15分）
(2)
$x^x=e^{x\ln x}$ （1分）
$\mathrm{d}(x^x)=(\ln x+1)x^x\mathrm{d}x$ （2分）
$\sqrt[x]{x}=e^\frac{\ln x}{x}$ （3分）
$\mathrm{d}(\sqrt[x]{x})=\frac{1-\ln x}{x^2}\sqrt[x]{x}\mathrm{d}x$ （4分）
$\dfrac{\frac{1-\ln x}{x^2}\sqrt[x]{x}}{(\ln x+1)x^x}周=\int_0^θ\dfrac{\mathrm{d}θ}{(1+a\cosθ)^2}$ （5分）
(i)$x=\frac{1}{e},\ln x+1=0,原式无意义$ （6分）
(ii)$x=e,1-\ln x=0,周获得自由,θ=0$ （7分）
(iii)$x\ne\frac{1}{e}且x\ne e,周=\dfrac{x^2(\ln x+1)x^x}{(1-\ln x)\sqrt[x]{x}}\int_0^θ\dfrac{\mathrm{d}θ}{(1+a\cosθ)^2}$ （8分）
下面求$\int_0^θ\frac{\mathrm{d}θ}{(1+a\cosθ)^2}$
椭圆的焦半径公式$r=\frac{1}{1+a\cosθ}$
$A=\frac{1}{1-a^2},B=\frac{1}{\sqrt{1-a^2}},C=\frac{a}{1-a^2}$
$α=\arcsin\frac{\sinθ\sqrt{1-a^2}}{1+a\cosθ}$ （9分）
$S=\frac{1}{2}αAB-\frac{1}{2}C\frac{\sinθ}{1+a\cosθ}$
$\int_0^θ\frac{\mathrm{d}θ}{(1+a\cosθ)^2}=2S$
$\int_0^θ\frac{\mathrm{d}θ}{(1+a\cosθ)^2}=\frac{1}{1-a^2}[\frac{1}{\sqrt{1-a^2}}\arcsin\frac{\sinθ\sqrt{1-a^2}}{1+a\cosθ}-\frac{a\sinθ}{1+a\cosθ}]$ （10分）
为什么我总是在发答案之后才看到题
好哒（三个字）
2024/3/13，本帖移出题目互答
二、【答案】$\dfrac{5\pi}{2}$
【解析】
三、【答案】
四、【答案】30°
【解析】
在AC上取点F，使BC=BF
根据角度关系，得∠ABC=∠ACB=80°，∠CBF=20°，∠ABF=60°，∠BCD=50°，∠ACD=30°
∴△BDF是等边三角形，BD=DF，∠ADF=120°，∠AFD=40°
在AC上取点G，使DF=DG
根据角度关系，得∠DGC=∠BEC=40°，DG//BE
∴BD:BE=DG:BE=AD:AB=AD:AC，∠DBE=∠DAC=20°
∴△DBE∽△DAC
∴∠BED=∠ACD=30°
@即未用户2448 的同学大佬的做法
难集上好像有个积分是e＞1，也是这个积分，是不是发散了，还是说用解析延拓
佬高考怎么样
下面那个20°的几何题和中点60°我初中做过，第一个叫兰利问题，第二个倍长一下
还有如果1+ecosθ是一次方怎么算
大佬！看来我的钓鱼题难不倒你
（6个月前出的题，当时还有很多人研究积分，现在的论坛。。。）
你来做我的每日一题吗？（现在是真没人了。。。）
现在没太多空了，听课听累了一定来试试
现在确实是没人了……别说研究积分了，等九月份考完高三几个主力退掉
我们又要重新开始了，说过来也快一年了你
