（共四题，略高于预赛难度）

Level 3 做题人数统计（截至2024/9）：共3人参与做题，第一题（轮轴）1人，第二题（滑轮）1人，第三题（斜面）0人，第四题（相对加速度）0人

Level 3 做题建议：独立完成，将解题过程发在评论区（注意这里是Level 3，不要发错了），最好反馈一下题目难度和做题用时

Level 3 题目评价：主要考查动力学问题的分析能力、计算能力、分类讨论；前三题以简单机械为情境，考查动力学模型；第四题考查相对运动与加速度的易错点

第一题 轮轴（40分）

如图，外半径为R，内半径为r，质量忽略不计的轮轴被锁住不能转动，轮轴与绳子间的摩擦因数为$\mu$，物块1,2的质量分别为$m_1,m_2$，重力加速度为g

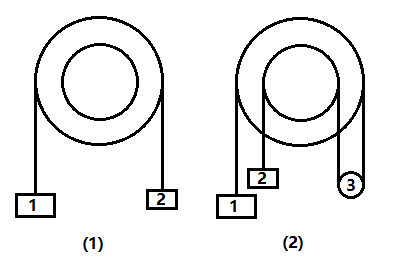
(1)（16分）如图(1)，若$m_1$>$m_2$，分别求物块1,2的加速度（向上为正，下同）

(2)（12分）如图(2)，若光滑圆盘3的质量为$m_3$，且物块1向下运动，物块2向上运动，分别求1,2,3的加速度

(3)（12分）如图(2)，若光滑圆盘3的质量为$m_3$，解除轮轴锁定，轮轴可以自由转动，且轮轴与绳子间没有相对滑动，分别求1,2,3的加速度

第二题 滑轮（40分）

如图，整个装置处于绕过O点的竖直轴匀速转动的水平面内，角速度为ω。物块1,2的质量分别为$m_1,m_2$，分别被限制在轨道1,2上运动，两轨道相互垂直，且与O点的距离均为r。用长为3r的绳子通过滑轮连接物块1和2，绳子保持伸直，滑轮在两轨道交点，滑轮大小忽略不计，重力加速度为g

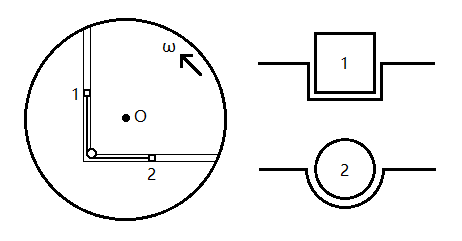
(1)（20分）若两轨道光滑，初始时物块1,2到滑轮的距离相等，静止释放并开始计时，求物块速度大小v、绳子张力T与时间t的关系（不需要求t的范围）

提示：微分方程$\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}=k^2(y-C)$的解为$y=Ae^{kx}+Be^{-kx}+C$，其中$A,B$为待定常数

(2)（20分）若轨道与物块间的摩擦因数为$\mu$，且轨道与物块1,2的横截面分别如图所示，物块1,2能保持静止，求物块1到滑轮的距离$x_1$的范围，以及绳子张力T与$x_1$的关系

第三题 斜面（40分）

如图，质量为M、倾角为θ且足够长的斜面放在光滑水平面上，质量为m的滑块可视为质点，斜面与滑块间的摩擦因数为$\mu$，重力加速度为g

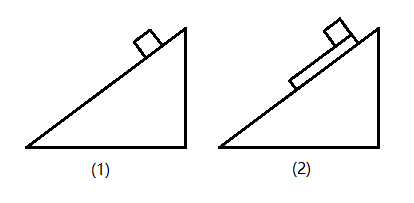
(1)（16分）如图(1)，静止释放，求斜面的加速度大小a、和滑块相对斜面的加速度大小a'

(2)（24分）如图(2)，在滑块与斜面之间增加一块长为$L=0.75~\mathrm{m}$、质量为$2m$的木板，木板厚度忽略不计（滑块滑下木板瞬间速度不变），滑块与斜面之间光滑（即$\mu=0$），滑块与木板间的摩擦因数为$\mu_1=0.5$，斜面与木板间的摩擦因数为$\mu_2=0.75$，倾角θ=37°  ($\tan\theta=0.75$)，$M=3m$，$g=10~\mathrm{m/s^2}$，滑块初始位置在木板顶端，静止释放并开始计时，求斜面的速度大小v与时间t的关系

第四题 相对加速度（40分）

如图，小球可视为质点，质量分别为$M,m_1,m_2$，放在光滑水平面上，用轻绳连接，长度分别为$l_1,l_2$，初始时静止

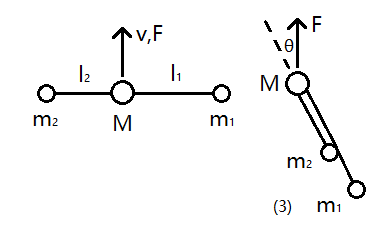
(1)（10分）若断开$l_2$，突然给M一打击，使其获得一速度v，同时给M施加力F，方向均垂直于$l_1$，求打击后瞬间$m_1$相对M的加速度大小

(2)（15分）若突然给M一打击，使其获得一速度v，同时给M施加力F，方向均垂直于轻绳，求打击后瞬间M的加速度大小

(3)（15分）设$l_1$>$l_2$，若系统运动一段时间后，如图(3)，小球$m_2$与轻绳$l_1$发生碰撞，此时$m_1,m_2$相对M的速度大小分别为$v_1,v_2$，力F与轻绳延长线的夹角为θ，求碰撞后瞬间M的加速度大小

$\color{red}答案解析$

还没做题的不要往下翻！

第一题 轮轴（40分）

(1)（16分）

轮轴与绳子间有摩擦，对一小段绳子受力分析

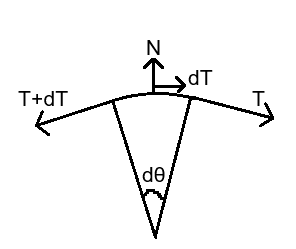
$(T+T+\mathrm{d}T)\sin\dfrac{\mathrm{d}\theta}{2}=N$  （2分）

$\mathrm{d}T=\mu N$  （2分）

$\mathrm{d}T$与$\mathrm{d}\theta$的乘积是高阶小量，可以忽略，得到

$\mu\mathrm{d}\theta=\dfrac{\mathrm{d}T}{T}$  （2分）

解微分方程，得 $T_1=T_2e^{\mu\pi}$  （2分）

若 $m_1\le m_2e^{\mu\pi}$，则无法发生相对滑动，$a_1=a_2=0$  （2分）

若 $m_1\gt m_2e^{\mu\pi}$，对物块1,2列动力学方程

$\begin{cases}T_1-m_1g=m_1a_1\\T_2-m_2g=m_2a_2\\a_1=-a_2\end{cases}$  （4分）

解得 $a_1=-a_2=-\dfrac{m_1-m_2e^{\mu\pi}}{m_1+m_2e^{\mu\pi}}g$  （2分）

(2)（12分）

注意绳子的运动方向，同(1)的方法，得（注意圆盘3是光滑的，圆盘3两侧的绳子张力相等，记为$T_3$）

$T_1=T_3e^{\mu\pi}=T_2e^{2\mu\pi}$  （2分）

物体1,2,3由一条绳子关联着，它们加速度的关系为（可以由位置的关系求两次导得到）

$a_3=-\dfrac{a_1+a_2}{2}$  （2分）

物体1,2,3的动力学方程

$\begin{cases}T_1-m_1g=m_1a_1\\T_2-m_2g=m_2a_2\\2T_3-m_3g=m_3a_3\end{cases}$  （2分）

联立，解得

$a_1=\dfrac{-m_1m_3-4m_1m_2e^{\mu\pi}+3m_2m_3e^{2\mu\pi}}{m_1m_3+4m_1m_2e^{\mu\pi}+m_2m_3e^{2\mu\pi}}g$  （2分）

$a_2=\dfrac{3m_1m_3-4m_1m_2e^{\mu\pi}-m_2m_3e^{2\mu\pi}}{m_1m_3+4m_1m_2e^{\mu\pi}+m_2m_3e^{2\mu\pi}}g$  （2分）

$a_3=\dfrac{-m_1m_3+4m_1m_2e^{\mu\pi}-m_2m_3e^{2\mu\pi}}{m_1m_3+4m_1m_2e^{\mu\pi}+m_2m_3e^{2\mu\pi}}g$  （2分）

(3)（12分）

轮轴与绳子间没有相对滑动，则$a_1,a_2$与轮轴角加速度的关系为

$\beta=\dfrac{a_1}{R}=\dfrac{a_2}{r}$  （2分）

物体1,2,3由一条绳子关联着，(2)中求出的 $a_3=-\dfrac{a_1+a_2}{2}$ 仍然适用  （2分）

轮轴质量忽略不计，力矩平衡

$T_1R+T_2r=T_3(R+r)$  （2分）

物体1,2,3的动力学方程仍然为 $\begin{cases}T_1-m_1g=m_1a_1\\T_2-m_2g=m_2a_2\\2T_3-m_3g=m_3a_3\end{cases}$

联立，解得

$a_1=\dfrac{-4m_1R^2-4m_2Rr+2m_3R(R+r)}{4m_1R^2+4m_2r^2+m_3(R+r)^2}g$  （2分）

$a_2=\dfrac{-4m_1Rr-4m_2r^2+2m_3r(R+r)}{4m_1R^2+4m_2r^2+m_3(R+r)^2}g$  （2分）

$a_3=\dfrac{2m_1R(R+r)+2m_2r(R+r)-m_3(R+r)^2}{4m_1R^2+4m_2r^2+m_3(R+r)^2}g$  （2分）

第二题 滑轮（40分）

(1)（20分）

设物块1,2到滑轮的距离分别为$x_1,x_2$，则 $x_1+x_2=3r$  （1分）

求二阶导，得到物块1,2的加速度关联 $a_1+a_2=0$  （1分）

以转动的水平面为参考系，物块1,2受到的惯性离心力的切向分量（远离滑轮为正方向）分别为 $\begin{cases}F_1=m_1\omega^2(x_1-r)\\F_2=m_2\omega^2(x_2-r)\end{cases}$  （2分）

物块1,2的动力学方程为 $\begin{cases}m_1\omega^2(x_1-r)-T=m_1a_1\\m_2\omega^2(x_2-r)-T=m_2a_2\end{cases}$  （2分）

联立以上公式，消去$T,x_2,a_2$，得 $\omega^2[(m_1+m_2)x_1-(m_1+2m_2)r]=(m_1+m_2)a_1$  （2分）

解微分方程，得 $x_1=\dfrac{m_1+2m_2}{m_1+m_2}r+Ae^{\omega t}+Be^{-\omega t}$  （2分）

求导，得 $v_1=A\omega e^{\omega t}-B\omega e^{-\omega t}$  （2分）

代入初始条件 $v_1(0)=A\omega-B\omega=0$，得 $A=B$  （2分）

代入初始条件 $x_1(0)=\dfrac{m_1+2m_2}{m_1+m_2}r+A+B=\frac{3}{2}r$，得 $A=B=\dfrac{m_1-m_2}{4(m_1+m_2)}r$  （2分）

代入$A,B$，速度大小取绝对值，得 $v=|v_1|=\dfrac{|m_1-m_2|}{4(m_1+m_2)}\omega r(e^{\omega t}-e^{-\omega t})$  （2分）

联立物块1,2的动力学方程和加速度关联，消去$a_1,a_2$，再代入$x_1+x_2=3r$，得 $T=\dfrac{m_1m_2\omega^2r}{m_1+m_2}$  （2分）

(2)（20分）

物块1,2受到的惯性离心力垂直轨道的分量分别为 $m_1\omega^2r$， $m_2\omega^2r$  （1分）

则物块1,2受到摩擦力的最大值分别为 $\begin{cases}f_1=\mu m_1(g+\omega^2r)\\f_2=\mu m_2\sqrt{g^2+(\omega^2r)^2}\end{cases}$  （4分）

实际摩擦力小于最大值 $\begin{cases}|F_1-T|\le f_1\\|F_2-T|\le f_2\end{cases}$  （1分）

当物块1有远离滑轮运动的趋势，临界情况 $\begin{cases}F_1-T=f_1\\T-F_2=f_2\end{cases}$

解得 $x_1=\dfrac{m_1+2m_2}{m_1+m_2}r+\dfrac{\mu m_1(g+\omega^2r)+\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2}$  （2分）

当物块2有远离滑轮运动的趋势，临界情况 $\begin{cases}T-F_1=f_1\\F_2-T=f_2\end{cases}$

解得 $x_1=\dfrac{m_1+2m_2}{m_1+m_2}r-\dfrac{\mu m_1(g+\omega^2r)+\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2}$  （2分）

所以$x_1$的取值范围为 $\dfrac{m_1+2m_2}{m_1+m_2}r-\dfrac{\mu m_1(g+\omega^2r)+\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2}\le x_1\le\dfrac{m_1+2m_2}{m_1+m_2}r+\dfrac{\mu m_1(g+\omega^2r)+\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2}$  （2分）

物块的运动趋势优先由摩擦力抵消，绳子张力$T$会尽可能小

当$T$最小时，临界情况 $\begin{cases}F_1-T=f_1\\F_2-T=f_2\end{cases}$

消去$T$，解得 $x_1=\dfrac{m_1+2m_2}{m_1+m_2}r+\dfrac{\mu m_1(g+\omega^2r)-\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2}$  （1分）

但是$T$不能小于0，当$T=0$时，临界情况 $F_1=f_1$ 或 $F_2=f_2$

解得 $x_1=r+\dfrac{\mu(g+\omega^2r)}{\omega^2}$ 或 $2r-\dfrac{\mu\sqrt{g^2+(\omega^2r)^2}}{\omega^2}$  （2分）

$T$与$x_1$的关系：

(i) 当 $2r-\dfrac{\mu\sqrt{g^2+(\omega^2r)^2}}{\omega^2}\le x_1\le r+\dfrac{\mu(g+\omega^2r)}{\omega^2}$ 时（该区间可能不存在）

$T=0$  （1分）

(ii) 当 $\dfrac{m_1+2m_2}{m_1+m_2}r-\dfrac{\mu m_1(g+\omega^2r)+\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2}\le x_1\le\min\{2r-\dfrac{\mu\sqrt{g^2+(\omega^2r)^2}}{\omega^2},\dfrac{m_1+2m_2}{m_1+m_2}r+\dfrac{\mu m_1(g+\omega^2r)-\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2}\}$ 时

$T=F_2-f_2=m_2\omega^2(2r-x_1)-\mu m_2\sqrt{g^2+(\omega^2r)^2}$  （2分）

(iii) 当 $\max\{\dfrac{m_1+2m_2}{m_1+m_2}r+\dfrac{\mu m_1(g+\omega^2r)-\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2},r+\dfrac{\mu(g+\omega^2r)}{\omega^2}\}\le x_1\le\dfrac{m_1+2m_2}{m_1+m_2}r+\dfrac{\mu m_1(g+\omega^2r)+\mu m_2\sqrt{g^2+(\omega^2r)^2}}{(m_1+m_2)\omega^2}$ 时

$T=F_1-f_1=m_1\omega^2(x_1-r)-\mu m_1(g+\omega^2r)$  （2分）

（以上所有结果默认$0<x_1<3r$）

第三题 斜面（40分）

(1)（16分）

水平方向对整体列牛顿第二定律，得 $Ma+m(a-a'\cos\theta)=0$  （3分）

对m分别沿斜面方向和垂直斜面方向列牛顿第二定律，得 $\begin{cases}-mg\sin\theta+\mu N=m(a\cos\theta-a')\\N-mg\cos\theta=-ma\sin\theta\end{cases}$  （5分）

解得，当M和m有相对滑动（$\mu\lt\tan\theta$）时

$a=\dfrac{mg\cos\theta(\sin\theta-\mu\cos\theta)}{M+m\sin\theta(\sin\theta-\mu\cos\theta)}$  （3分）

$a'=\dfrac{(M+m)g(\sin\theta-\mu\cos\theta)}{M+m\sin\theta(\sin\theta-\mu\cos\theta)}$  （3分）

当M和m无相对滑动（$\mu\ge\tan\theta$）时， $a=a'=0$  （2分）

(2)（24分）

第一阶段（滑块在木板上）： 木板与斜面之间无相对滑动  （2分）

证明： 若有相对滑动，因为 $\mu_2=\tan\theta$，所以木板对斜面的作用力（正压力与摩擦力的合力）竖直向下，斜面受到水平方向的合力为0，斜面静止，木板和滑块整体受到水平方向的合力也为0，不会向下滑动  （3分）

把木板和斜面看作一个整体，应用(1)中的结论（代入 $M=5m$，$\mu=0.5$），得

$\begin{cases}a_1=\frac{5}{16}~\mathrm{m/s^2}\\a_1'=\frac{75}{32}~\mathrm{m/s^2}\end{cases}$  （4分）

$t_1=\sqrt{\frac{2L}{a_1'}}=0.8~\mathrm{s}$  （1分）

第二阶段（滑块滑下木板）： 木板与斜面之间有相对滑动  （2分）

证明： 若无相对滑动，因为 $\mu_2=\tan\theta$，所以斜面对木板作用力（支持力与摩擦力的合力）的水平分量不可能向右，但斜面向右加速运动，所以木板不可能跟斜面一起运动  （3分）

虽然滑块和木板的加速度不同，但我们可以把滑块和木板看成整体来应用(1)中的结论，其中$m$替换为总质量$3m$，$\mu$替换为平均摩擦因数 $\bar{\mu}=\dfrac{\mu_2(2m)}{m+2m}=0.5$  （2分）

（你也可以把牛顿第二定律的方程都列出来，不难验证该方法的正确性，其实用类似这种简化运算的方法最好都验证一下）

应用(1)中的结论（将$M,m$分别替换为$3m,3m$，代入 $\mu=0.5$），得

$a_2=\frac{10}{7}~\mathrm{m/s^2}$  （3分）

所以 $v=\begin{cases}\frac{5}{16}t,~~~~~~~~~~~~0\le t\le0.8~\mathrm{s}\\\frac{10}{7}t-\frac{25}{28},~~~~t\gt0.8~\mathrm{s}\end{cases}$  （4分）

第四题 相对加速度（40分）

(1)（10分）

（图中x轴沿轻绳向右，y轴垂直轻绳向上）

以M为参考系，打击后瞬间$m_1$相对M的速度大小也为$v$，-y方向，绕M做圆周运动  （2分）

所以$m_1$相对M的加速度的x分量为$a_x'=-\dfrac{v^2}{l_1}$  （2分）

在惯性参考系中，M在y方向的加速度为$a_y=\dfrac{F}{M}$  （2分）

以M为参考系，$m_1$受到-y方向的惯性力，切向加速度为$a_y'=-a_y=-\dfrac{F}{M}$  （2分）

所以$m_1$相对M的加速度大小为 $a'=\sqrt{a_x'^2+a_y'^2}=\sqrt{(\dfrac{v^2}{l_1})^2+(\dfrac{F}{M})^2}$  （2分）

(2)（15分）

M在y方向的加速度仍为$a_y=\dfrac{F}{M}$  （2分）

在x方向上，由(1)的方法得 $\begin{cases}a_{1x}'=-\dfrac{v^2}{l_1}\\a_{2x}'=\dfrac{v^2}{l_2}\end{cases}$  （3分）

相对加速度与绝对加速度的关系 $\begin{cases}a_{1x}'=a_{1x}-a_x\\a_{2x}'=a_{2x}-a_x\end{cases}$  （3分）

整体在x方向不受力， $Ma_x+m_1a_{1x}+m_2a_{2x}=0$  （2分）

解得

$a_x=\dfrac{(m_2l_1-m_1l_2)v^2}{(M+m_1+m_2)l_1l_2}$  （3分）

$a=\sqrt{a_x^2+a_y^2}=\sqrt{(\dfrac{(m_2l_1-m_1l_2)v^2}{(M+m_1+m_2)l_1l_2})^2+(\dfrac{F}{M})^2}$  （2分）

(3)（15分）

M在垂直轻绳方向的加速度为$a_\perp=\dfrac{F\sin\theta}{M}$  （1分）

碰撞时速度不变，碰撞后瞬间$m_1$相对$m_2$的速度大小为 $v_1+v_2$  （1分）

(i) $l_2$绷紧

沿轻绳方向的相对加速度（$m_1$指向M为正方向）

$\begin{cases}a_{12}'=a_1-a_2=\dfrac{(v_1+v_2)^2}{l_1-l_2}\\a_2'=a_2-a_{//}=\dfrac{v_2^2}{l_2}\end{cases}$  （3分）

沿轻绳方向对整体列牛顿第二定律，得

$Ma_{//}+m_1a_1+m_2a_2=F\cos\theta$  （1分）

解得

$a_{//}=\dfrac{F\cos\theta-(m_1+m_2)\dfrac{v_2^2}{l_2}-m_1\dfrac{(v_1+v_2)^2}{l_1-l_2}}{M+m_1+m_2}$  （2分）

$l_2$绷紧的条件： $a_2\ge0$  （1分）

$a_2=a_{//}+\dfrac{v_2^2}{l_2}=\dfrac{F\cos\theta+M\dfrac{v_2^2}{l_2}-m_1\dfrac{(v_1+v_2)^2}{l_1-l_2}}{M+m_1+m_2}\ge0$

解得 $F\cos\theta+M\dfrac{v_2^2}{l_2}\ge m_1\dfrac{(v_1+v_2)^2}{l_1-l_2}$  （1分）

$a=\sqrt{(\dfrac{F\cos\theta-(m_1+m_2)\dfrac{v_2^2}{l_2}-m_1\dfrac{(v_1+v_2)^2}{l_1-l_2}}{M+m_1+m_2})^2+(\dfrac{F\sin\theta}{M})^2}$  （1分）

(ii) 当 $F\cos\theta+M\dfrac{v_2^2}{l_2}\lt m_1\dfrac{(v_1+v_2)^2}{l_1-l_2}$ 时，$l_2$松弛

用(i)的方法，把$m_2$替换为轻绳$l_1$上与M的距离为$l_2$的点，点的质量为0

所以只要把(i)中的结果中的$m_2$替换为0

$a=\sqrt{(\dfrac{F\cos\theta-m_1\dfrac{v_2^2}{l_2}-m_1\dfrac{(v_1+v_2)^2}{l_1-l_2}}{M+m_1})^2+(\dfrac{F\sin\theta}{M})^2}$  （4分）