物理 常微分算符5 第五阶段
如果后面已经有了$D^{n-k}$, 那么在前面就得有(n-k)个括号取D,作用在后面的函数上。如果剩下的k个括号全取Q,那么这些Q的下标$i_1,i_2,\dots,i_k$. 就能取完所有可能的组合。当然要注意不能重复:$\sum\limits_{i_1=1}^{n-k+1}\sum\limits_{i_2=i_1+1}^{n-k+2}\cdots\sum\limits_{i_k=i_{k-1}+1}^{n}\prod\limits_{j=1}^{k}Q_{i_j}$. 然而,剩下的k个括号并不是非得全取Q, 取D但是不作用在最后的函数上,作用在后面的某个Q上不也行吗?现在我们在其中(r-1)个括号中取D, 剩下(k-r+1)个中取Q. 那么Q的下标就会直接从$i_r$开始取到$i_k$. (因为$i_1\sim i_{r-1}$变成了D. )用打撇表示求导,那么我们总共可以在Q上打(r-1)个撇。现在用$x_j$表示第j个撇打在了哪个$Q_{i_j}$上,且使每一个x都不小于前一个。(可能等于,因为一个Q上可以有很多个撇。)我们的目标是:给定$x_1\sim x_{r-1}$, 即给定撇的分布,求有多少种D的作用方式满足这种分布。例:$(D+Q_1)(D+Q_2)(D+Q_3)(D+Q_4)$前两个括号取D后两个括号取Q,那么$Q_3'Q_4'$前面的系数应该是2,因为可能是第一个D作用在$Q_3$上,第二个D作用在$Q_4$上;也有可能是第一个D作用在$Q_4$上,第二个D作用在$Q_3$上。对于$Q_3$和$Q_4$各打一撇这种分布,有两种可能的情况,所以最后一定会出现$2Q_3'Q_4'$这一项,称重数为2。
第j次打撇,是在$Q_{i_{x_j}}$上打撇。我们想知道有多少个D可能用来贡献这一个撇。可以用来打撇的只能是前面的D,前面有$(i_{x_j}-1)$个括号,而其中$(x_j-r)$个括号已经取了Q. 已经打过$(j-1)$个撇,消耗了$(j-1)$个D. 所以可能贡献撇的D就有$(i_{x_j}-x_j+r-j)$个。重数就让j从1取到(r-1)全部乘起来即可。但请注意:同一个Q上面打的多个撇不可分辨!道理很简单,$D^2Q$最后只会出来一个$Q''$, 而不是2个. 而我们前面是按照撇可分辨来算的,所以要除去交换数。$Q_{i_j}$上打了多少个撇呢?$\sum\limits_{l=1}^{r-1}\delta_{x_l,j}$. 应该很好理解吧!遍历一遍,每有一个x等于j就令总次数+1, 否则不变(+0)。
所以结果就是n个方程构成的方程组:
$$\begin{cases}P_1=\sum\limits_{i=1}^nQ_i\\P_k=\sum\limits_{r=1}^k\sum\limits_{x_1=r}^k\sum\limits_{x_2=x_1}^k\cdots\sum\limits_{x_{r-1}=x_{r-2}}^n\sum\limits_{i_r=1}^{n-k+r}\sum\limits_{i_{r+1}=i_r+1}^{n-k+r+1}\cdots\sum\limits_{i_k=i_{k-1}+1}^n\left[\prod\limits_{j=1}^{r-1}(i_{x_j}-x_j+r-j)\prod\limits_{j=r}^k\dfrac{Q_{i_j}^{(\sum_{l=1}^{r-1}\delta_{x_l,j})}}{(\sum_{l=1}^{r-1}\delta_{x_l,j})!}\right],k=2\sim n\end{cases}$$
暂且不论我们写出来的这个严格的在n取任何正整数时都成立的式子,给定一个n,如何快速写出答案呢?乖乖按照上面那个式子求和、求积肯定是不现实的,我们不太会遇到n很大的情况,算个3阶、4阶就绰绰有余了。我们以4阶为例,看一下快速写出系数的办法。
前面两个没什么问题。D²的系数,先把所有两个Q可能的组合全部列出来。
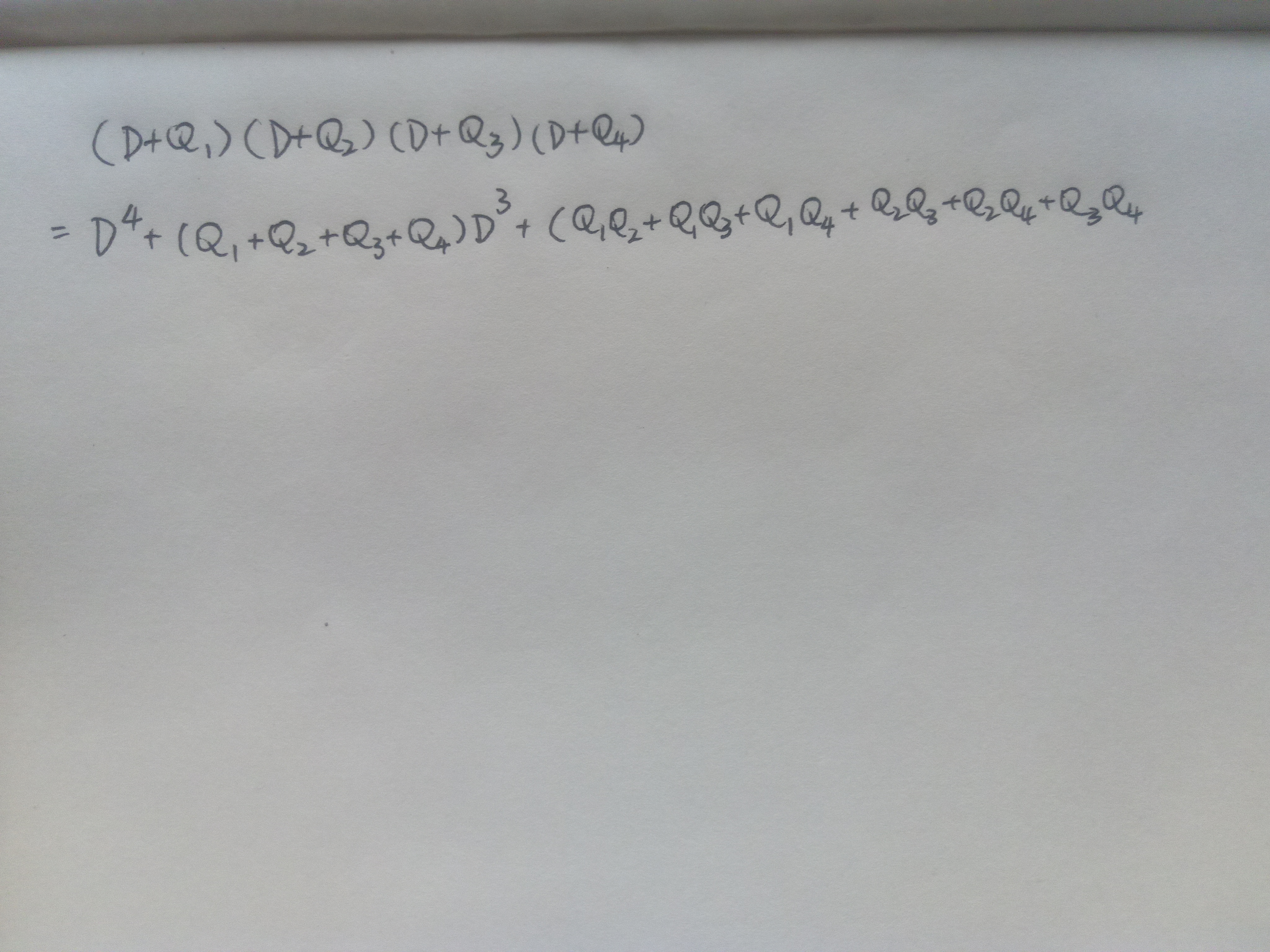
然后对每一个组合,以划去前面的Q的代价在后面的Q上打撇。把所有可能的情况加到系数里。这样D²的系数就写完了。
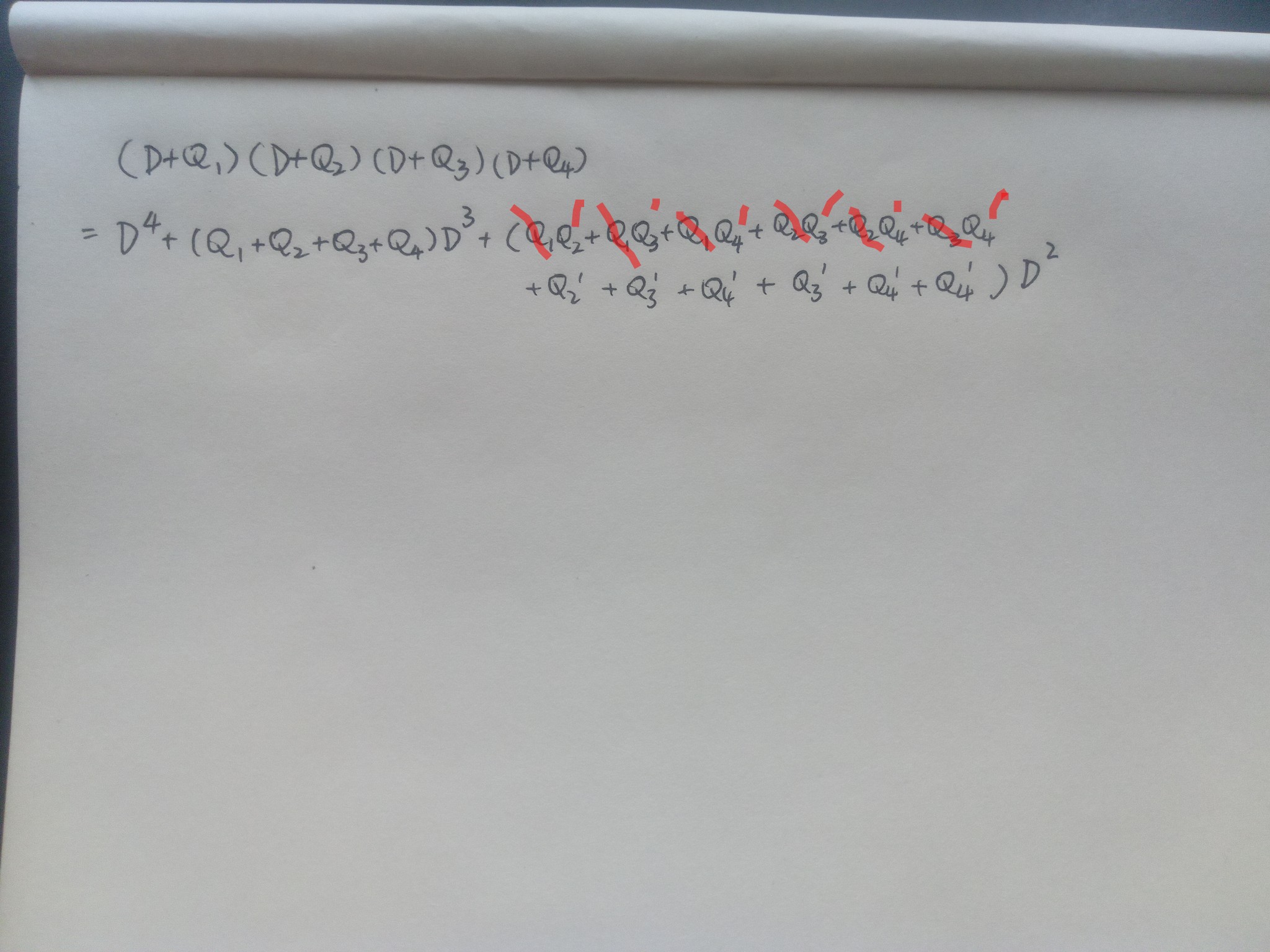
D的系数同样先写出4项。每一项都有4中可能的划Q方式,所以每一个组合都会产生4个附加项,全部加到系数里。

常数项自然就是4个Q之积了,然后我们慢慢划。先只划一个Q。

然后划两个Q。注意划去Q₁Q₂时会产生2个Q₃'Q₄'.
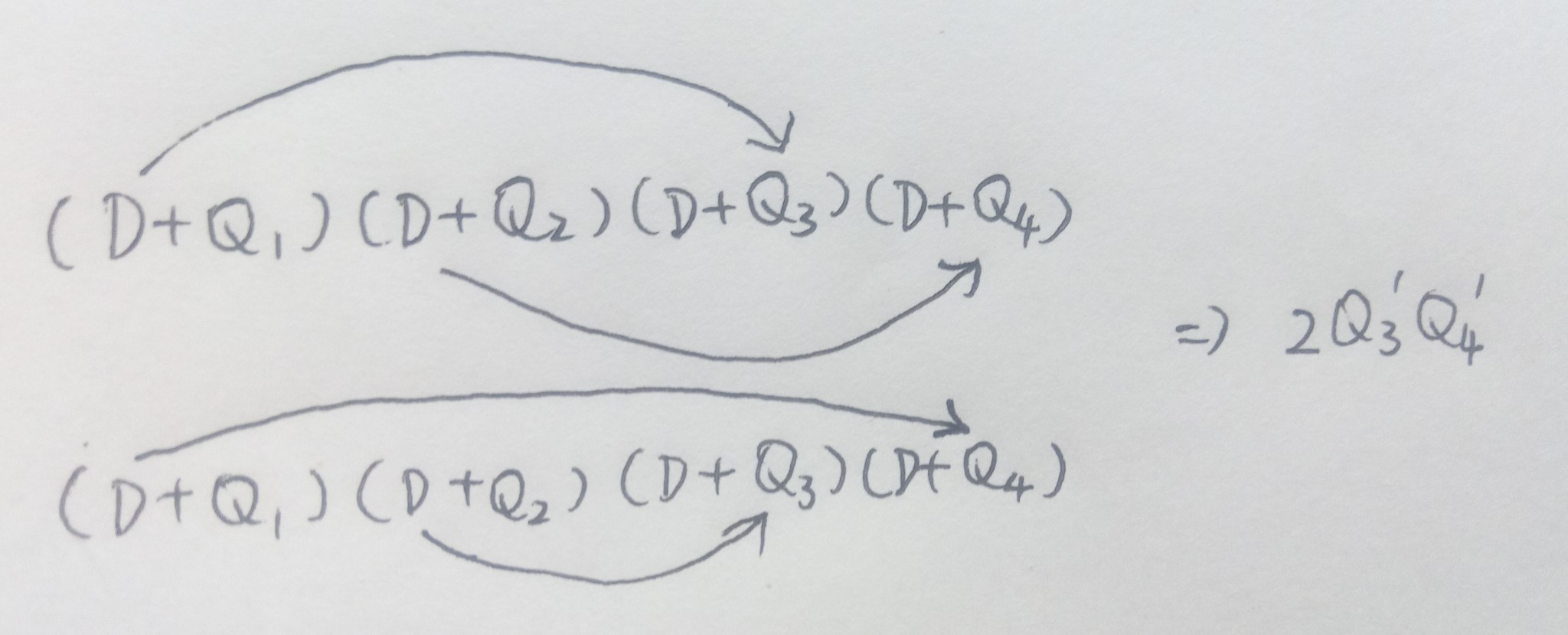
而两个撇打在同一个地方时就不会出现这个问题.
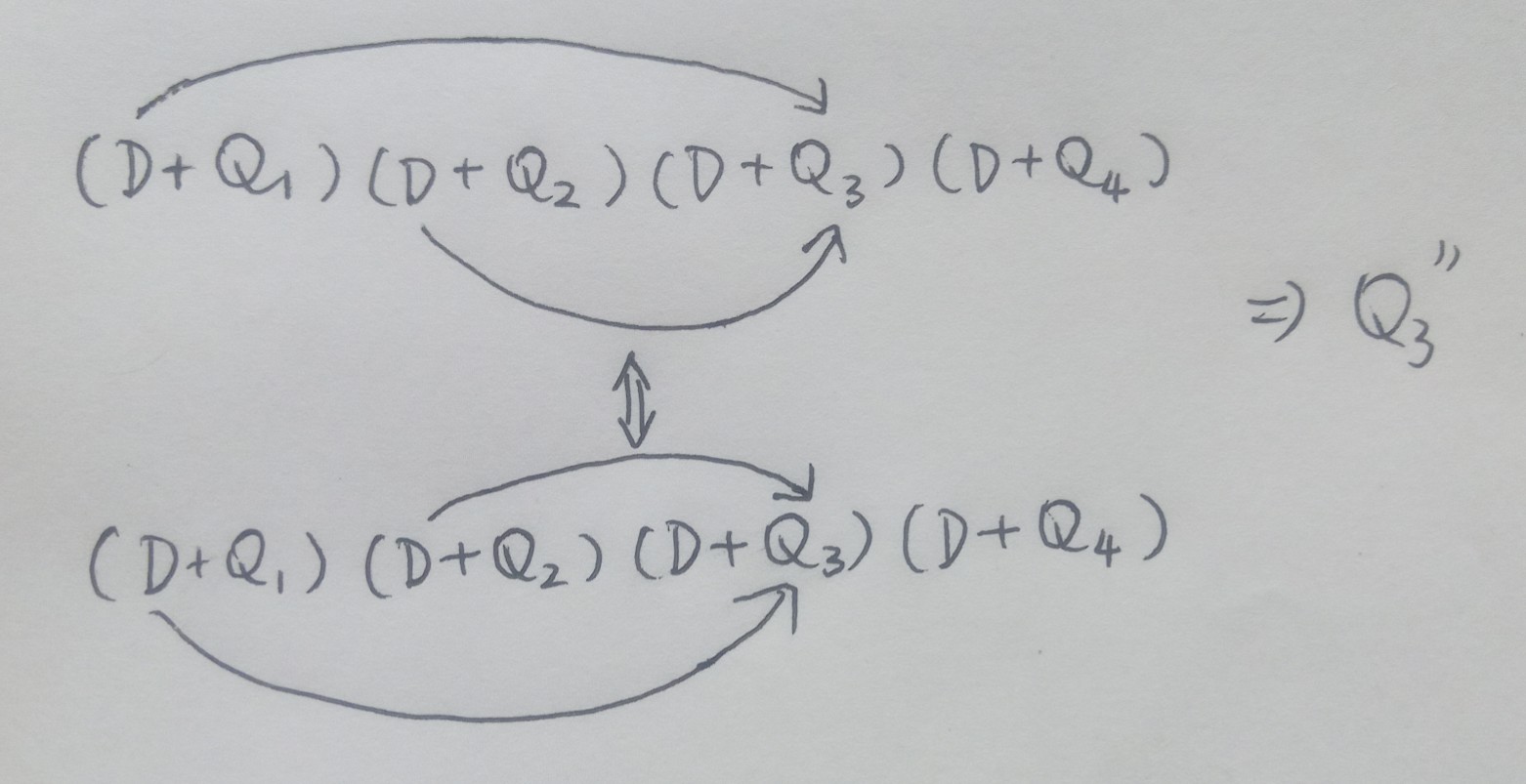
划去Q₁Q₃时也不会产生这个问题.
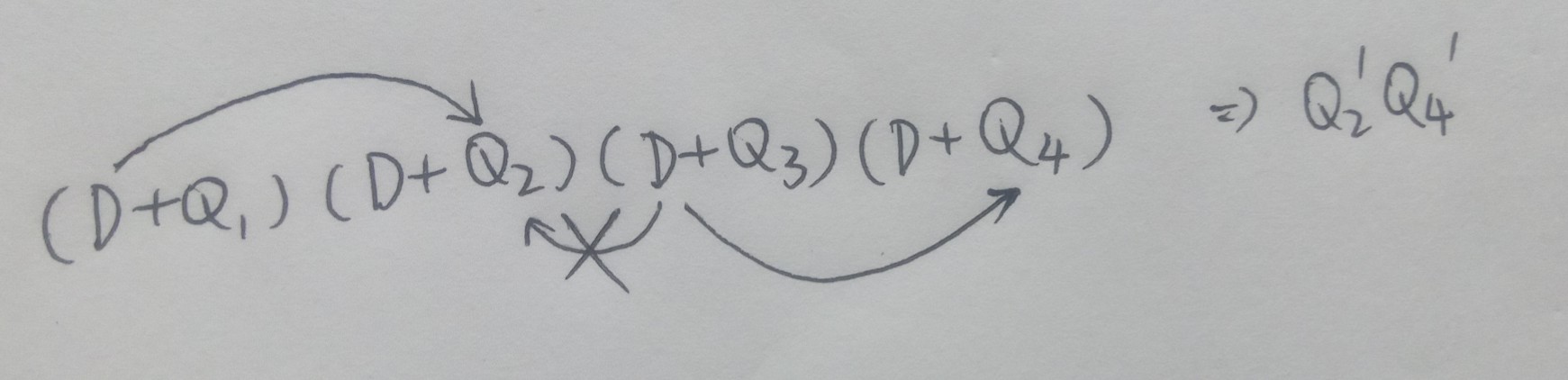
划去三个Q自然只能是Q₄'''. 总之把所有项加起来,把相同的项合并就得到开篇给出的结果。
现在我们来代一下特殊的情形看看,即练17欧拉方程,两边除以$x^n$就得到$P_k=P_kx^{n-k}$. (重字母了,难受。不过大家应该都能看懂,我就不改了。左边的P指一个函数,右边的P是常数。)
然后发现:次数非常整齐。每对x求一次导就乘一个x回来,第k个方程全为x的-k次。自然猜$Q_i=\frac{A_i}{x}$. 很容易联立n个方程就把$A_i$解出来了。而换元t=ln x也很能理解了,大概就像$\dfrac{x\mathrm{d}}{\mathrm{d}x}=\dfrac{\mathrm{d}}{\mathrm{d}\ln x}$这样化为常系数。

