物理

常微分算符3

我们把对单元函数求导的操作视为一个算符作用在函数上，即为「常微分算符」(Ordinary Differential Operator, ODO)，一般用D表示。常微分算符是一个线性算符，能做四则运算，于是我们可以用她来巧妙地解决一些微分方程。然而，由于是线性算符，所以无法用于非线性微分方程，除非你利用换元等手段将其转化为线性微分方程。但无所谓，物理竞赛基本不要求非线性微分方程。在常微分算符1和常微分算符2中，我们已经用常微分算符解决了一些问题。这里介绍常微分算符的另一实用功能：快速解耦。

例8：第二届CPHO-S物理联考第5题 电磁感应与振动

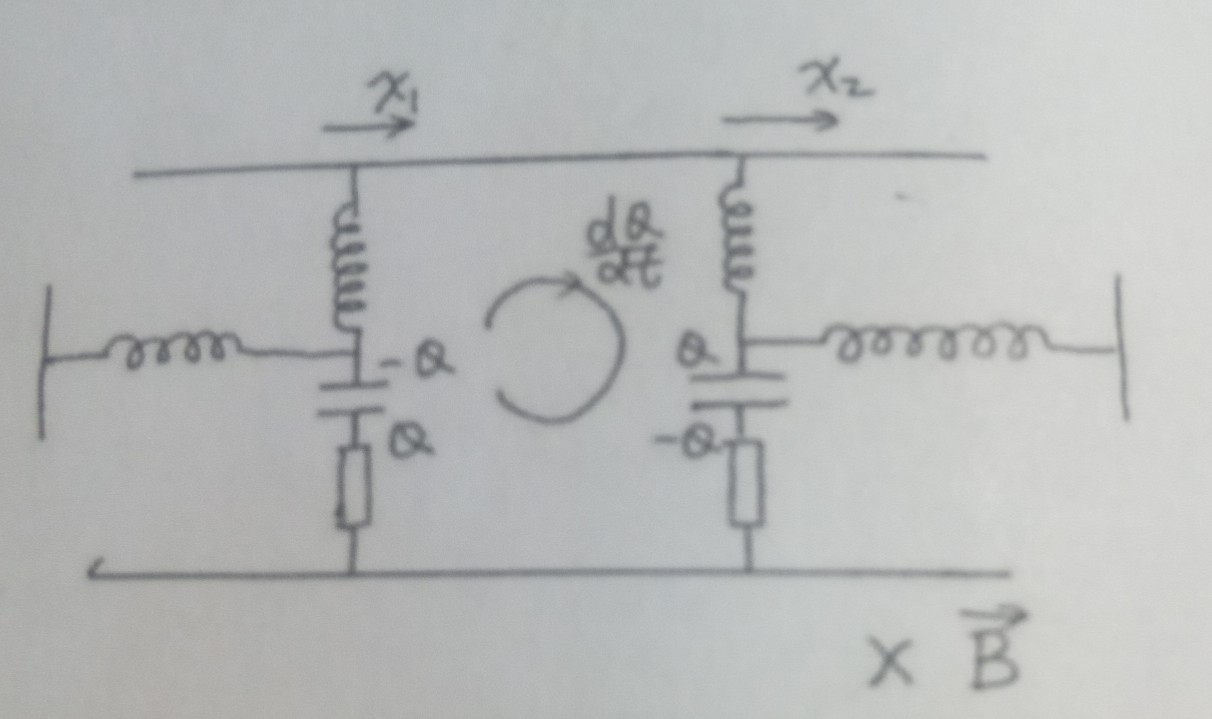
如图所示的光滑导轨上放置有两根金属棒，其间距为l。导轨的电阻可以忽略，金属棒上接有电阻R、电感L、电容C，且金属棒与两侧的固定隔板有劲度系数为k的不导电弹簧连接，空间中存在如图所示的匀强磁场。左、右两棒偏离平衡位置的坐标分别记为x₁、x₂；电容器上带有的电荷记为Q；各个坐标的方向如图所示。

已知R=1Ω, L=1H, C=0.5F, B=1T, m=1kg, k=1kg/s², l=1m. 初态x₁=0m, x₂=1m, v₁=1m/s, v₂=0m/s, Q=1C, $\frac{dQ}{dt}$=1A.

求$x_1(t), x_2(t), Q(t)$.

先列运动方程

$$m\ddot x_1=-kx_1-Bl\dfrac{\mathrm{d}Q}{\mathrm{d}t}$$

$$m\ddot x_2=-kx_2+Bl\dfrac{\mathrm{d}Q}{\mathrm{d}t}$$

回路方程$$2L\dfrac{\mathrm{d}^2Q}{\mathrm{d}t^2}+2R\dfrac{\mathrm{d}Q}{\mathrm{d}t}+\dfrac{2}{C}Q=-Bl(\dot x_2-\dot x_1)$$

两个运动方程相加，消去Q：$$m(\ddot x_1+\ddot x_2)=-k(x_1+x_2)$$

利用初始条件迅速得到：$$x_1+x_2=\sin x+\cos x$$

现在，欲消去回路方程中的$x_1-x_2$，为此令$\xi=x_1-x_2$，并引入常微分算符$D=\dfrac{\mathrm{d}}{\mathrm{d}t}$

两个运动方程相减：$$(mD^2+k)\xi=-2BlDQ$$

移项：$$\xi=-\dfrac{2BlDQ}{mD^2+k}$$

代入回路方程：$$2LD^2Q+2RDQ+\dfrac{2}{C}Q+\dfrac{2B^2l^2D^2Q}{mD^2+k}=0$$

注意到$(mD^2+k)0=0$，得到$$mLD^4Q+mRD^3Q+(\frac{m}{C}+kL+B^2l^2)D^2Q+kRDQ+\frac{k}{C}=0$$

代入数据：$$Q^{(4)}+Q^{(3)}+4\ddot Q+\dot Q+2=0$$

解出特征根：

$$\lambda_{1,2}=-0.0730275\pm 0.779584i$$

$$\lambda_{3,4}=-0.426973\pm 1.75496i$$

则$$Q(t)=Q_1\sin(0.779584t)e^{-0.0730275t}+Q_2\cos(0.779584t)e^{-0.0730275t}+Q_3\sin(1.75496t)e^{-0.426973t}+Q_4\sin(1.75496t)e^{-0.426973t}$$

现在确定四个待定常数。首先就有$Q(0)=1,\dot Q(0)=1$. 其次通过$\xi(0)=-1$与$\dot\xi(0)=1$得到$\ddot Q(0)=-\dfrac{5}{2},Q^{(3)}(0)=0$

很快就能解出$$Q_1=0.7149,Q_2=0.4703,Q_3=0.4007,Q_4=0.5297$$

后面的过程我就不写了，解出ξ后得到

$$x_1=\dfrac{x_1+x_2+\xi}{2}$$

$$x_2=\dfrac{x_1+x_2-\xi}{2}$$

总之我想说的就是，面对耦合的微分方程的时候，直接利用常微分算符把其中一个量解出来，带入另一个式子强行消元。非常好用。