物理

元素周期表

很好很好，加油！

浅浅问一下怎样插入能在平板上直接打开的帖子链接🤔

弱弱的问一句@质心小姐姐这个可以申质选吗…… 

$\int_{-\infty}^{\infty} \frac{\partial^{\alpha+\beta+\gamma}}{\partial x^{\alpha}\partial y^{\beta}\partial z^{\gamma}} \left[ \exp\left( -\frac{1}{2} \begin{pmatrix} x & y & z \end{pmatrix} \begin{bmatrix} \sigma_x^2 & \rho_{xy}\sigma_x\sigma_y & \rho_{xz}\sigma_x\sigma_z \\ \rho_{xy}\sigma_x\sigma_y & \sigma_y^2 & \rho_{yz}\sigma_y\sigma_z \\ \rho_{xz}\sigma_x\sigma_z & \rho_{yz}\sigma_y\sigma_z & \sigma_z^2 \end{bmatrix}^{-1} \begin{pmatrix} x \\ y \\ z \end{pmatrix} \right) \times \prod_{k=1}^{n} \left( \frac{1}{\sqrt{2\pi}\sigma_k} \int_{-\infty}^{\infty} e^{-\frac{(w_k-\mu_k)^2}{2\sigma_k^2}} \frac{\Gamma(\alpha_k+\beta_k)}{\Gamma(\alpha_k)\Gamma(\beta_k)} w_k^{\alpha_k-1} (1-w_k)^{\beta_k-1} dw_k \right) \times \sum_{m=0}^{\infty} \frac{(-1)^m}{(2m)!} \left( \frac{\hbar^2}{2m_e} \nabla^2 \right)^m V(\mathbf{r}) \Psi(\mathbf{r},t) - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \left( \nabla \times (\nabla \times \mathbf{A}) + \mu_0 \epsilon_0 \frac{\partial^2 \mathbf{A}}{\partial t^2} \right) + \lim_{N \to \infty} \prod_{p=1}^{N} \left( 1 + \frac{1}{p^s} \sum_{n=1}^{\infty} \frac{\mu(n)}{n^s} \prod_{q=1}^{m} \zeta(s+\alpha_q) \right) \times \det \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \cdots & \frac{\partial f_n}{\partial x_n} \end{pmatrix} + \oint_C \frac{f(z)}{(z-a)^{n+1}} dz - \frac{2\pi i}{n!} f^{(n)}(a) + \frac{1}{\sqrt{-g}} \frac{\partial}{\partial x^\mu} \left( \sqrt{-g} g^{\mu\nu} \frac{\partial \Phi}{\partial x^\nu} \right) + m^2 c^2 \Phi + \mathrm{Tr} \left[ \gamma^\mu (i\partial_\mu - eA_\mu) - m \right] \psi + \frac{1}{Z} \int \mathcal{D}[\phi] \exp\left( i \int d^4x \mathcal{L}(\phi, \partial_\mu \phi) \right) \langle \Omega | T \{ \phi(x) \phi(y) \} | \Omega \rangle + \sum_{k=1}^{\infty} \frac{B_{2k}}{(2k)!} x^{2k-1} + \frac{1}{\Gamma(s)} \int_0^{\infty} t^{s-1} \left( \frac{1}{e^t-1} - \frac{1}{t} + \frac{1}{2} \right) dt + \frac{1}{2\pi i} \oint_\gamma \frac{f'(z)}{f(z)} dz - (N-P) + \nabla \cdot \left( \rho \mathbf{v} \otimes \mathbf{v} + p \mathbb{I} - \mu (\nabla \mathbf{v} + (\nabla \mathbf{v})^T) \right) - \rho \mathbf{g} + \frac{d}{dt} \frac{\partial L}{\partial \dot{q}_i} - \frac{\partial L}{\partial q_i} - Q_i + R_{\mu\nu} - \frac{1}{2} R g_{\mu\nu} + \Lambda g_{\mu\nu} - \frac{8\pi G}{c^4} T_{\mu\nu} + i\hbar \frac{\partial}{\partial t} \Psi - \left[ -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}) + \frac{e\hbar}{2mc} \boldsymbol{\sigma} \cdot \mathbf{B} \right] \Psi + \frac{1}{\beta} \frac{\partial}{\partial J} \ln Z[J] - \langle \phi \rangle + \oint_{\partial M} \omega - \int_M d\omega \right] dxdydz = 0$

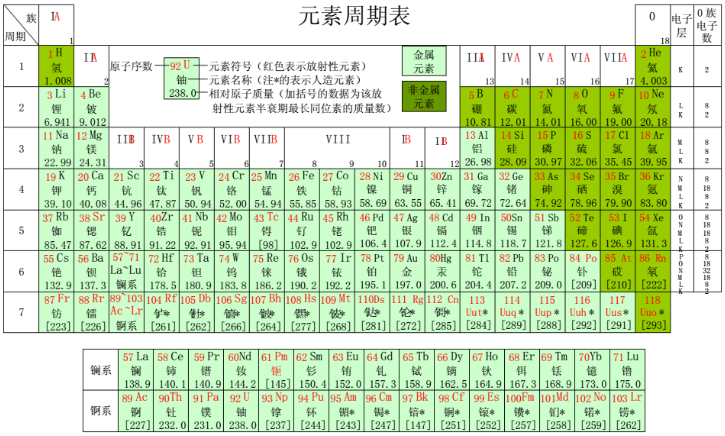
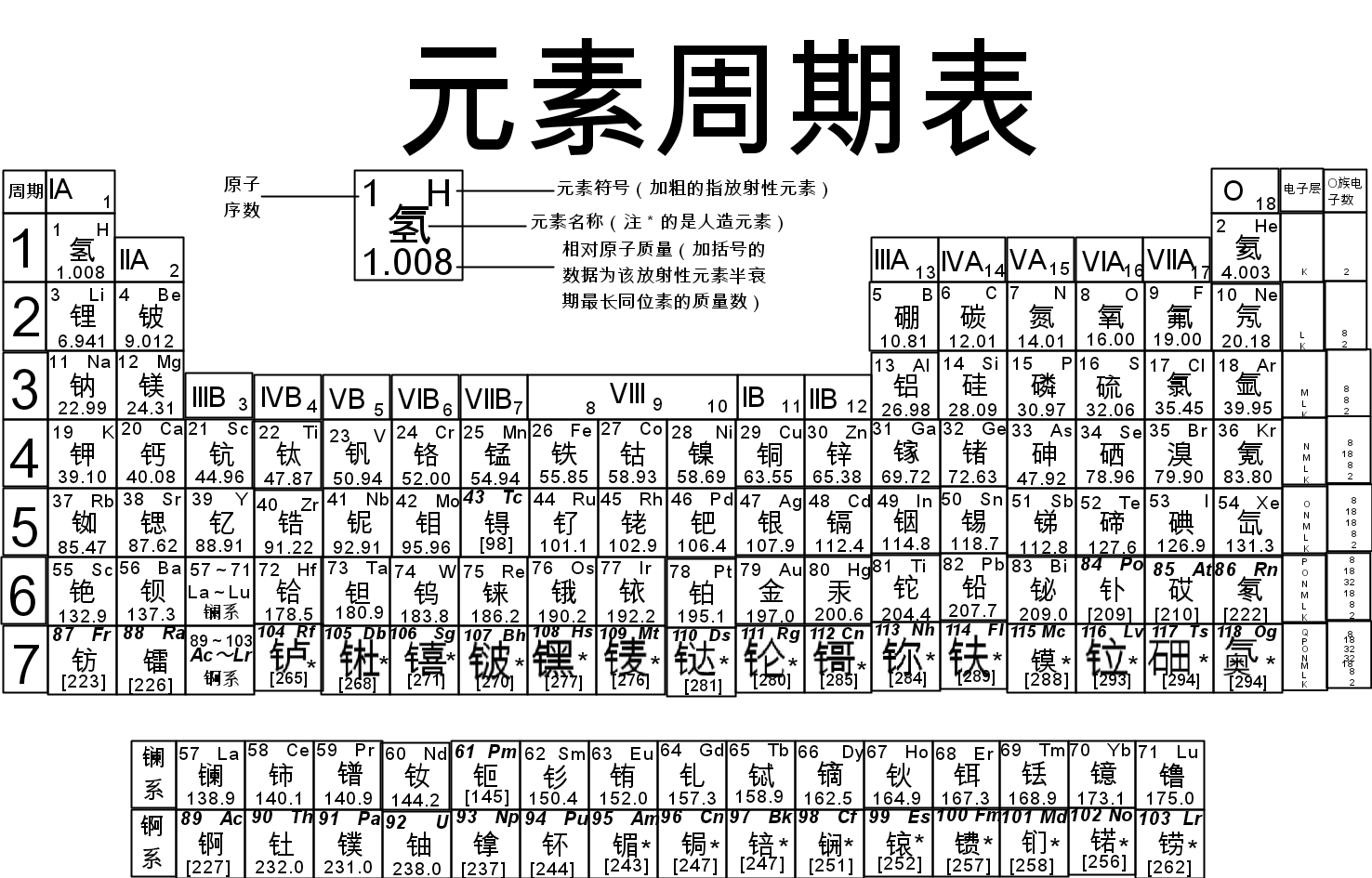有点粗糙😅