数学

数学板块新手轮+基础轮+预备轮+衔接内容

说明:在下墨霜那帖子无法打开,最新内容见此贴或墨霜衍生帖.

此内容不局限于新手轮....欢迎观看。。。一些可能在后面;先行说明〔称为先导〕，[通常在函数上很好使用]单调性为单调递增或单调递减;

对数的概念:若a^x=N(a>0且a≠1，称指数式):x＝log(a)N;(称对数式)；

基本恒等式:log(a)1=0;对数恒等式:a^log(a)N=N;特殊对数:①以10为底:log(10)N=lgN;2:以自然对数(e=2.718....)为底:写作In N;

衍生公式:log(a)b*log(b)a=1; log(a)b*log(b)c*log(c)d*log(d)e*log(e)f*log(f)g=log(a)g; log(a)b+log(a)c=log(a)bc.   ;log(a)b-log(a)c=log(a)b/c;

综合log(a^m)b^n=n/m*log(a)b;

三角函数公式:(sin α)^2＋(cos α)^2=1

函数平行变换:左加右减上减下加;[切勿反对,初中学名上加下减]上面点的坐标y轴相加,为了不变,而减.

切记1在任何时候都是绝杀招

符号科普 ∀任意，∅空集、∈属于、∏相似于∑、不过第二个是求和，第一个是阶乘

开始正题:

1:因式分解;

1. 找到同类项提取公因数
2. 公式法
3. 十字交叉法合并

2:函数:

1. 一次函数:y=ax+b[表达式] 图像在b=0时与数轴x,y交于一点原点.b!=0时与数轴x,y各交于一点.
2. 二次函数:y=ax^2+bx+c.    图像在a>0时开口向上,a<0时开口向下.
3. 三角函数:sin在0~90时向上,90~180时向下在此区间的sin(x)皆∈[0.,1].180~360∈[-1,0]在超过360后角度默认为n-360*[n/360].[单独补充在后]
4. 高次函数:图像渐渐相似.
5. 反比例函数:y=k/x;又名双曲线,在此函数图像上任意一点的坐标(x,y)都满足xy=k;[见9，可知此函数为α=-1时的图像.

3:不等式:

1. 一次不等式;只需记住除法的时候的数为负数时符号变号即可.最坑的是分类讨论对系数分类讨论.

4.几何:

      1.三角形的性质: 

             1.三边关系:a+b>c,b+c>a,c+a>b;

             2.四心:其实还有个旁心,不过不想算在里面.四心分别为重心(G),外心(O),内心(I),垂心(H).

             3.特殊三角形:例如直角三角形[勾股定理],等边三角形[三线合一,四心共点,三角60度]

             4.全等:

                         1:SSS(边边边) 

                         2:SAS(边角边)

                         3:ASA(角边角)  

                         4:AAS(角角边) 

                         5:HL(实际上算是SAS特殊情况) 

              5.相似:

                         1:AA(角角,毕竟AA与AAA没区别)

                         2:SAS(等比例的边,角)

        2.平行四边形:

               1.定义:两组对边平行时为平行四边形.

               2.有5种判断是否为平行四边形的方法:

                         1:以边来判断:

                                    1:两组对边平行时

                                    2:一组对边平行且相等时

                                    3:两组对边相等时

                          2:以角来判断:

                                    1:两组角相等时

                          3:以对角线来判断:

                                    1:两条对角线互相平分;

            2.计算平行四边形的面积:

                           1:S平行四边形＝相邻两边与其夹角正弦乘积.

                           2:S平四=底乘高.

         3:勾股定理:

                           1:直角三角形:a^2+b^2=c^2;

                           2:广义勾股定理:在任意三角形ABC上以AB为底做一条高起垂足为D.设AB=c,AC=b,BC=a,AD=d,CD=e则可得到:c^2=a^2+b^2±2ae.

         4:菱形:具有平行四边形所有性质;

                           1:四条边长度相等;

                           2:对角线互相平分且互相垂直.

                           3:对角线亦为角平分线.

                    2:判定:

                           1.四条边相等

                           2.关于两条对角线为对称轴.

             5.矩形:

                           1.矩形的四个内角皆为90度.     

                           2.矩形两条对角线相等并互相平分.

              6.正方形[特殊矩形,特殊菱形,特殊平行四边形]:

                            1.具有矩形,平行四边形,菱形的一切性质.

              7.无敌中位线:

                             1.在三角形和梯形最为常用.

              8.圆

                              1.作为无限多条边的图形,圆,有很多定理:

                              2.基本不常考,考了基本不会,在此不做介绍,只需记住此图形的对称性,正余弦关系即可.

4.一元二次方程:

         1.因式分解

         2.公式

         3.韦达定理[有实根先]

5.分式:

定义:分母下有未知数变为分式.

求分式时切记分母不为0

6.线段最值看将军饮马.

7.祝各位考好成绩.打在公屏上[求了]

恒接内容开始------------------------------------------------

8.集合:

1.集合的性质:

集合有确定性，互异性，与无序性三性质.通常错误率大部分在这上面了.

定义集合：A＝｛1，2，3，X38t50，4｝；B＝｛8，X38t50，1，12345，3｝

2:集合符号:

    1:交集（∩）A交B指集合A与B之间相同的元素[元素,指集合中的参数例如A中的1，2，X38t50等],举例:A∩B＝｛1，3，X38t50｝；

    2:并集（∪）A并B指集合A与B之间所有的元素,因为可能存在元素相等不满足于集合的互异性,于是A并B中指所有集合中的元素,重复的删去,只剩1个.

                           举例:A∪B＝｛1，2，3，4，8，12345，X38t50｝。

    3:差集（表示方法为:{x|x∈A 且x∉B｝）。亦可以记做B－A[或BA]。举例:BA={2，4}。

    4:补集（U:全集[包括A与B即可,至于外面想填什么元素任意。]）U－A＝>{Cu A＝｛x|x∈U∉A｝。

    5:集合的阶:集合A的元素个数由|A|来表示.

    6:集合的划分与覆盖:

         1:集合的划分,设一个集合A分为A1,A2...而集合的划分时划分的集合交集为空集.

         2:集合的覆盖,A=A1∪A2∪A3∪...∪An;而划分是覆盖的一种特殊情况;

    7:容斥原理.

        1:|A1∪A2|＝|A1|+|A2|-|A1∩A2|.

        n:|A1∪A2∪...∪An|=|A1|+|A2|+.....+|An|-两两相交+三三相交-...-（－1）的n+1次方＊n个相交;

    8:经典问题1:子集问题.

         设A＝｛a1，a2，...,an｝。

        1:子集个数:2的n次方；

        2:所有子集中的元素之和的总和:

                1:看每个元素出现次数:（a1＋a2＋...＋an)＊2的n-1次方;

                2:配对（组合的核心思想):互为补集之和为全集A,运用此思想可推出->对数共2的n-1次方,全集A为（a1＋a2＋...＋an)；

        3:奇子集与偶子集:

                奇子集的定义为元素之和为奇数;同理偶子集;

                得出结论:（1）奇子集个数为全集子集的一半（前提至少有一个奇数)

                                 （2）奇子集元素之和的总和:一半（前提至少两个奇数)

      9:经典问题二:元素互斥问题:

            广义方法:取其最大,使保证以上数接不违反题意，后筛出选择就违反题意得数,以此执行以上操作直到没有数;

     10:映射的概念:定义集合A与B;

            1:对于A中任意元素x，按照某种确定的对应法则f，都有B中唯一元素y与之对应，则称这种对应关系为A到B的一个映射;则当y＝f（x）？A为定义域,B为陪域;

               值域 f（A）＝｛y|y＝f（x）｝⊆陪域

            2:函数:定义A与B为数集[数字集合];可将函数抽象化:例如y=2x＋1;而x为A集合中的一个元素,y为B集合的一个元素,当元素一一对应便可形成函数.

            3:相等映射:1:定义域相同;2:对应关系相同;为充分必要条件.

            4:特殊映射:

                1:单射:A中不同元素在B中有不同的象:|A|<=|B|.

                2:满射:对于集合B中的任何元素,都在集合A中存在原象:|A|>=|B|.

                3:既单又满:|A|=|B|;

                4:逆映射:只有是既单又满的情况下反过来设才成立,也是逆映射的条件.

                5:复合映射:三个集合及以上以从左向右来疯狂映射

                详细映射见

9:超越函数:[特殊函数]

     1:幂函数与指数函数:

            条件:这两个函数皆在指数幂的条件下成立.

            1:幂函数:则知道一次函数，二次函数等多次函数[系数必为1]皆属于幂函数;

                    1:幂函数的特性:形如f(x)=x^α（α∈R）当α>1时,所有幂函数形态皆似二次函数,并且都过一个特殊点:(1,1);[第一象限]

                        同时由奇偶性(对称性:偶函数图像沿y轴对称,其特点为f(-x)=f(x);奇函数图像关于原点对称[特殊情况可能只有第一或四象限],其特征为:f(-x)=-f(x).)确定完整图像.

            2:指数函数:

                    1:形如f(x)=a^x[指数为变量,a>0且a≠1,x∈R]为指数函数.

                    2:分成两类:①:0<a<1:当x趋近于无限大,则值越接近于x轴[值越趋近于0]单调递减....见先导

                                         ②:a>1:单调递增...见先导

                                         综上:定义域为x∈R，值域(0,+∞);f(0)=a^0=1->过点(0,1).f(x)=a^x与f(x)=(1/a)^x关于y轴对称.

                    PS:此函数比较大小用一条直线按从高到低则为从大到小.

      3.对数函数:

            定义:形如f(x)=log(a)x[a>0且a≠1，x>0]为对数函数;与y=a^x互为反函数;关于y＝x对称;

            特殊点:1:0<a<1过(1,0)

                        2:a>1过(1,0)

            综上:定义域:(0,+∞)；值域为R;定点为(1,0);相对位置关系:在第一象限图像离y轴越远,底数越大.

            在运算过程中先导已记录，推倒公式亦在;

10:函数的单调性与奇偶性:

        1:函数的单调性:

                1.一次函数图像在定义区间内任意x1,x2;

                          1:x1<x2时存在f(x1)<f(x2)为单调递增;

                          2:x1>x2时存在f(x1)>f(x2)为单调递减.

                2.反比例函数图像在1,3象限时为单调递减,同时此线为x,y轴渐近线[指函数中的一个图像的一个点无限接近于无穷时两线之间距离无限近似于0;]

                                   此图像在2,4象限时为单调递增,同时此线为x,y轴渐近线[指函数中的一个图像的一个点无限接近于无穷时两线之间距离无限近似于0;]

        2:函数单调性判断:

               1:画图[分段函数]

               2:定义法∀x1<x2∈D:做差:f(x1)-f(x2){<0[单调递增];    >0[单调递减];};

       3:函数单调性四则运算:

              定义:↑＝增函数；↓＝减函数;

              则:↑＋↑＝↑;↓＋↓＝↓;

              所以推导出↑*（-1)=↓;↑－↓＝↑;

       4:判断复合函数[函数套函数]单调性:

              [切记基本知识:分母不为0,根号下大于等于0.........则以由内而外循循判断;而倒数会改变单调性;]

              判断法则:外层增,不影响内层单调性;外层减,内部单调性相反;

              PS:广泛运用于比较大小,解不等式,求最值/值域;

       5:函数的奇偶性:

              提取上层资料:奇函数关于原点对称,偶函数关于y轴对称;

              定义:∀x∈D，都有－x∈D;f(x)定义域要关于原点对称[一旦不是,此函数为非奇非偶函数];

              1:奇函数偶函数判断[先看定义域]:定义法:f(-x)=-f(x)---偶函数;f(-x)=-f(x)---奇函数;[详细介绍]

        6:函数的四则运算:

                    普通四则运算:奇＋奇＝奇,偶＋偶＝偶,奇+偶＝非奇非偶[可定义为未知]

                    中等四则运算:   ...h（g（f（x））））...遇偶则偶，全奇则奇;

                    常见题型:一直一边求另一边;

11:三角函数的概念与性质:

        1:任意角与弧度制:

                 设射线旋转度数为α;

                1:[任意角]定义:先行定义条射线,让其射线旋转任意方向任意度数[端点为定点],生出另一条射线,则为此角度数[讨论]:

                           1:顺时针旋转,度数为-α;2:逆时针旋转,度数为α;3:不旋转,为0度角;

                2:角度制,弧度制[以弧长定义一角].运用于比较角的大小;算法:用弧长/半径 来衡量教的大小,单位记做rad(可省略,毕竟没单位)

                           PS:弧度=兀相当于180度;45度=兀/4;

        2:单位圆[指半径为1的圆]，在平面直角坐标系上以原点为中心,画出一个单位圆,并任意定一个角[任意角性质]其中终边必于单位圆形成一交点;

            定义此交点为P(x,y);设此角度数为β;

               推论出:x=cosβ;y=sinβ;x/y=cotβ;y/x=tanβ;PS:根据此角这终边所在象限判断正负;

        3:三角函数的图像与性质:图像规律在上面以呈现,自行参考;

               图像周期性T＝2兀;[sin与cos];T=兀;[tan]

               而sin与tan为奇函数,cos为偶函数;

12:正弦型函数与图像变化:

        1:正弦型函数:

                1:形如f(x)=A sin(wx+φ)为正弦型函数;可推导出(x^2/k)＋y^2＝1[未来的椭圆方程]

                2:此函数的周期性与正弦函数周期性极其相似,周期性为|2兀/ω|

                3:轴对称:sin(ωx+φ)=±1→ωx+φ=π/2+kπ,k∈Z;

                4:中心对称:sin(ωx+φ)→ωx+φ=kπ,k∈Z;

                5:此函数单调性:[以复合函数来考虑:t＝ωx＋φ,y=Asin t;]ω>0;

                                            ↑:-π/2+2kπ≤t[ωx+φ]≤3/2π+2kπ;

                                            ↓:π/2+2kπ≤t[ωx+φ]≤3/2π+2kπ;k∈Z;

13.反三角函数见[三角函数][最近写的过于麻烦，所以有一些设置于另外一些帖子]

14.标量与矢量.[1]

标量的定义:只有大小没有方向的量[例如 路程]

矢量的定义:有大小也有方向的量.

标量遵循简单四则运算法则.

矢量的运算法则是平行四边形法则;

平行四边形法则如下图

15.位移;

路程的定义:质点[对运动无太大影响可视为一个点.]的实际运动路径的长度---属于标量.

位移的定义:描述位置变化的大小与方向.用符号$\overset→x$表示.而|$\overset→x$|表示为此位移大小.单位为m

同时,路程绝对不小于位移的大小。

16:斜率

其实在初中就已经接触过斜率了.

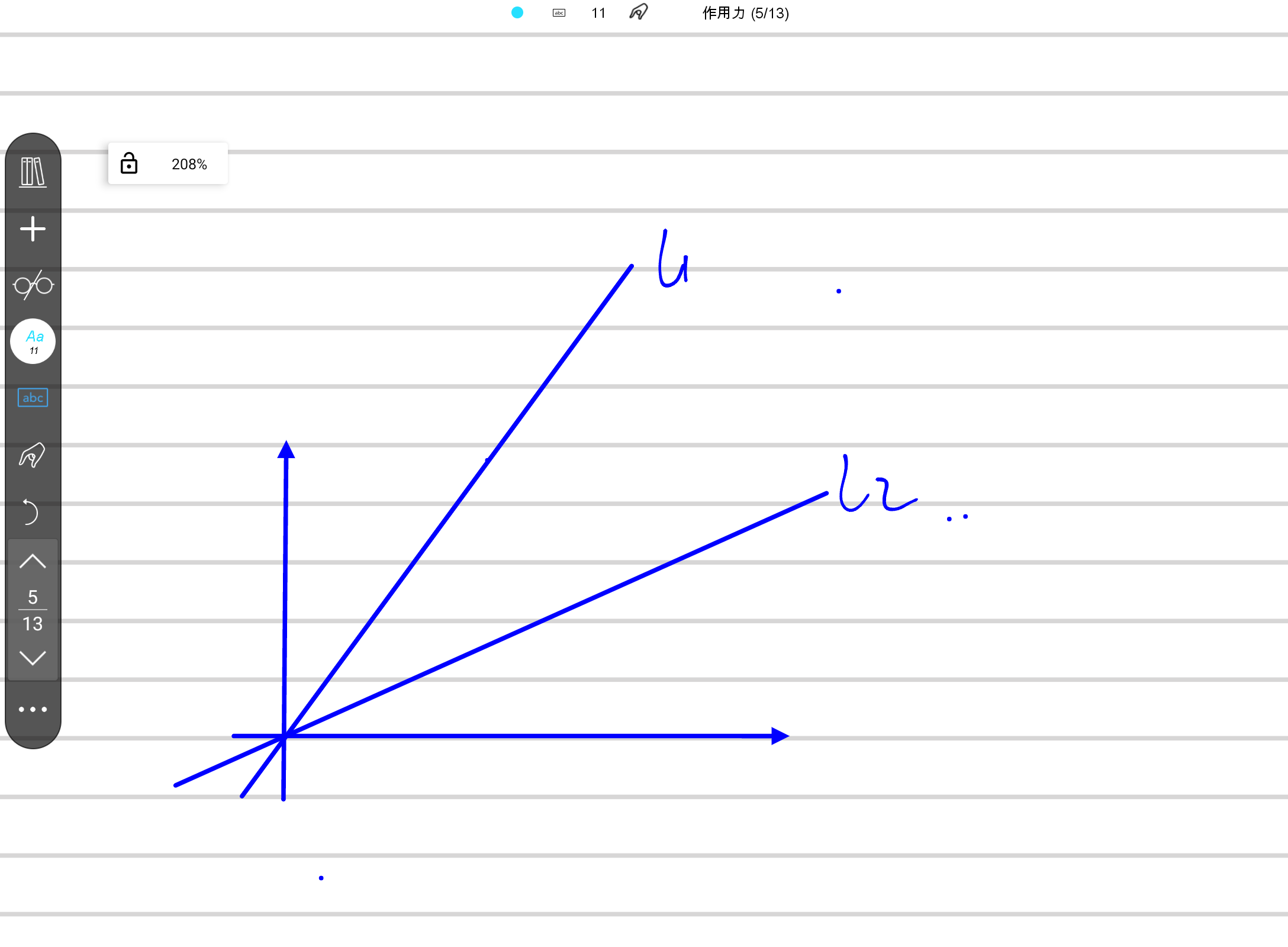
设定𝑙1l1​=𝑓(𝑥)=𝑘1𝑥(𝑘1≠0)f(x)=k1​x(k1​=0)

设定𝑙2l2​=𝑓(𝑥)=𝑘2𝑥(𝑘2≠0)f(x)=k2​x(k2​=0)

易见当k变大,随之函数斜率也变大.

则𝑘1k1​>𝑘2k2​。

快速求斜率的方法:节点法

在一条一次函数上任取两点,记为(𝑥1,𝑦1),(𝑥2,𝑦2)(x1​,y1​),(x2​,y2​)

可变为𝑘=(𝑦1−𝑦2)/(𝑥1−𝑥2)k=(y1​−y2​)/(x1​−x2​)斜率变为k.

如何求二次函数的斜率?

涉及到导数的定义:假设函数y=f(x)在点𝑥0x0​处的邻域内有定义.当自变量x在𝑥0x0​处取得增量Δx,相应的函数取得增量Δ𝑦Δy。

如果Δy／Δx在Δx→0时极限存在,那么称函数y＝f(x)在点𝑥0x0​处可导.概括为一个公式:𝑓‘(𝑥)=𝑙𝑖𝑚Δ𝑥→0Δ𝑦/Δ𝑥f‘(x)=Δx​→0lim​Δy​/Δx​

只要Δx无限趋近与0,就可以越接近于斜率了.

8.3继续补衔接内容[已完成]---------------------------------------------------------喜欢的给个赞。。。

8.7更新超越函数,目前此模块更新50％;

8.10更新正弦型函数,目前超越函数模块更新70％;

＠质心小姐姐,能通过计划吗;加个0.2不过分;@质心小姐姐 @质心小姐姐

编号:1

防盗标签:不是水帖;

原创