数学 数学新手轮1~10复习资料[2]
1.向量的定义与物理中的矢量可说是一模一样。矢量在物理中的定义是有方向大小的,此处向量亦是如此.现在讲述一下向量:
向量有很多法则,加法用三角形法则,平四[平行四边形]法则,多边形法则,见图片
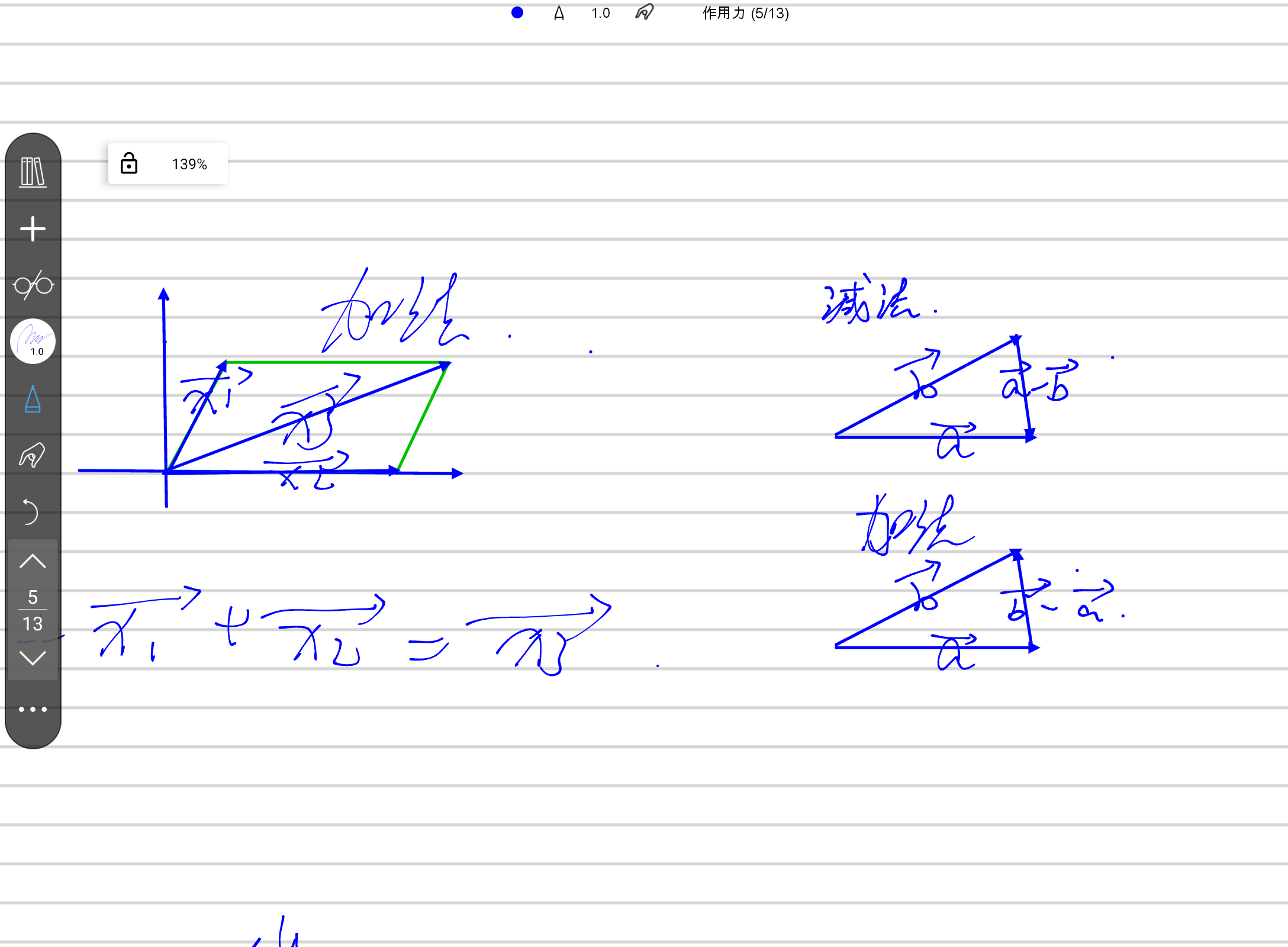
以上便是向量的计算方式.向量可以完美的将原先路程的无方向性给解决了,
但是切记路程不等于向量,向量无法与向量比较大小;路程不小于向量的模,向量的模可比大小
物理竞赛中,有方向又有大小的量称为矢量;
有大小没有方向的量称为标量;
信息竞赛中,结构体可以安插一些数据;
而以上的矢量与结构体便是数学中向量一种特殊方法.
物理的标量便是我们数学中的纯量或数量[过于重复,不常用]
而零向量是个特殊大小的向量,任意方向,大小为0,写法为$overset{0}{→}$
特殊方向的向量:当$a//b$则称这两向量为共线向量[平行向量][向量可以平行]
2:三角函数
初中:sin,cos,tan
初高中cot,sec,cec;
其中见表
30° 45° 60°
sin :$ rac{1}{2}$. $ rac{sqrt{2}}{2}$. $ rac{sqrt{3}}{2}$.
cos:$ rac{sqrt{3}}{2}$. $ rac{sqrt{2}}{2}$.$ rac{1}{2}$.
tan:$ rac{sin}{cos}$
cot:$ rac{1}{tan}$
sec:$ rac{1}{cos}$
cec:$ rac{1}{sin}$
高中:弧长制(rad) π=180°;
常用公式:
1诱导公式:共54个,9组;前五组为同名诱导公式,后四组为不同名诱导公式;[口令:奇变偶不变,符号看象限]
2正弦公式:sin(α±β)=sinαcosβ±sinβcosα;
3正切公式:tan(α±β)=(tanα干tanβ)/(1±tanαtanβ);
4:二被角公式:sin2α=2sinαcosα;
反三角函数:单调函数必有反函数,而三角函数不是单调函数[所以反三角函数[正弦]的表达式是 y=arcsinx=$sin^{-1}$x.
图像如图一;
arcsinx=y y∈[-π/2,π/2]-------------------------角
sin(arcsinx)=x,x∈[-1,1]----------------------------值
问:cos(arcsinx)=?
sin(arcsinx)=x;先前定义arcsinx=y
所以sin(y)=x;cos(y)=$sqrt(1-x^2)$.
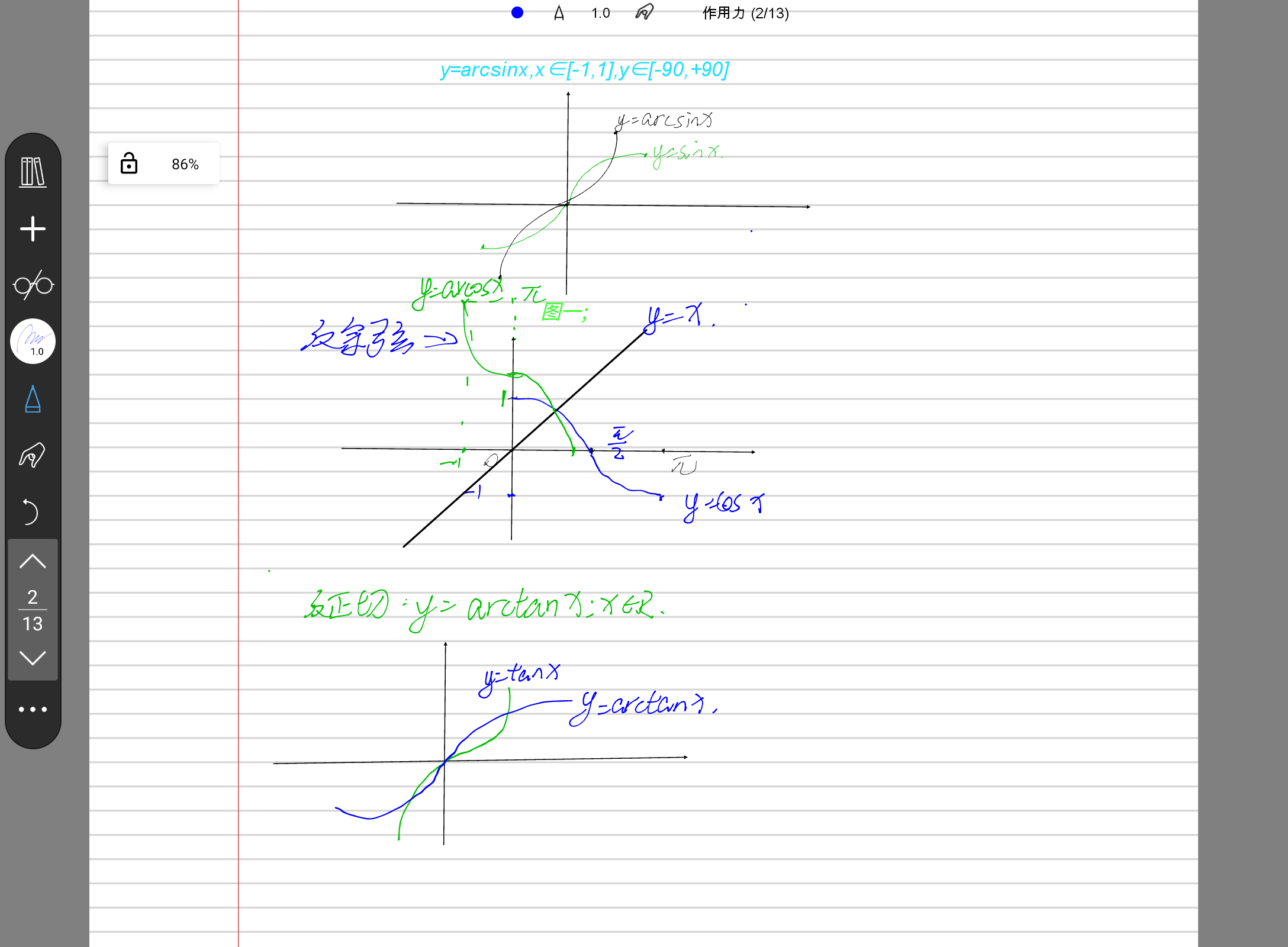
补充:已知tanarctanx=x;
设arctanx=y;
问sin(y)或cos(y)的值?
解:画三角形
如下图做三角形即可.

可得到答案;[arcsin相当于位移,则这里是求导,微积分]
四:三角方程:
sin x=a 1:|a|>1:$∅$
2:|a|=1:${x|x=2kπ+arcsin a,k∈Z}$
3:|a|<1:${x|x=kπ+((-1)^k)*arcsin a,k∈Z}$
cos x=a 1:|a|>1:$∅$
2:|a|=1:${x|x=2kπ+arccos a,k∈Z}$
3:|a|<1:${x|x=kπ+((-1)^k)*arccos a,k∈Z}$
tan x=a(a∈R):${x|x=kπ+arctan a,k∈Z}$
衔接内容结束,进入高中基础知识
3:复数的概念:
1:欧拉公式:$e^{iθ}=cosθ+isinθ$;当θ=π时,最美公式$e^{iπ}+1=0[因为这里有我们最常用的5个数[此处π为弧度制]$
2:复数的域与复数形式.:设z为复数,则z可表示为z=a+bi.而复数的域用C表示
4:数列:
1:数列的定义:按照一定的顺序排列的一列数.小学已学过数列的第一项称为:首项.
$//$而每次写的时候有多困难,大家都知道.于是现在定义数列为$a_1,a_2,a_3...a_n$所以第n项就为$a_n$;
2:数列的分类:
1:有穷数列:有一定数量的数列[有限]
2:无穷数列:有无穷数量的数列[无限]
3:递增数列:每项都不小于前一项即可;例:1,1,1,1,1,1,1,1,2;
4:严格递增数列:每一项都大于前一项;
5:递减数列:每一项不大于前一项;
6:严格递减数列:$a_i都小于a_{i-1}$[1<i];
7:摆动数列:无规律数列;
8:常数列:项数都相等.[平常数列];
3:数列表示方法:
1:条件:有规律的数列;例如:等差数列,等比数列等.
2:列通向[部分小学5年级内容,不写了,在写我像是个煞子(bushi;]
找通项先找到一定的规律,例如4,0,4,0..知道一会加四一会减四,但是可见,中间为2;则为$2-(-1)^n*2$
3:若瞪眼找不到,就用递推公式$a_n=ga_{n-k}+1[g,k∈Q]$
不等式高阶:
1:均衡不等式;均衡不等式的题,想简单就跟送分一样,想难就与送命相似;而不等式想要难会难成与不等式无关一样.[题目见另一贴[问题贴[8.31日发]]]
而均衡不等式最难的地方在于构造出类似均衡不等式的东西,而使用时找到规律便易如反掌,直接秒杀.这便是难点.
而对付此常用的一种方法便是把其他参数干掉,剩下一个便会比原本好看很多.随之也变得很简单[都初中了这东西应该都会了吧,不写出来了]
2:柯西不等式;
柯西不等式在初中叫叫可以,到高中别人听不懂.在高中又称施瓦茨不等式.
如这:$(a^2+b^2)(c^2+d^2)≥(Ac+bd)^2$
而柯西不等式极其高端,见如下
二维形式一般推广2式:
1:$\overset{1}{\underset{n}{∑{a_i}^2}\overset{1}{\underset{n}{∑{b_i}^2}≥(\overset{1}{\underset{n}{∑{a_i}^2{b_i}^2}$
2:$(x_1+y_1+...)(x_2+y_2+...)...(x_n+y_n+...)≥[(\overset{1}{\underset{n}{∑{x_i}})^{\tfrac{1}{2}}+(\overset{1}{\underset{n}{∑{y_i}})^{\tfrac{1}{2}}+...]^n$
向量形式推广:
$|a||b|≥|a·b|,a=(a_1,a_2+,...,a_n),b=(b_1,b_2,...,b_n)$
三角形式:
$\sqrt{a^2+b^2}+\sqrt{c^2+d^2}≥\sqrt{(a-c)^2+(b-d)^2}$
积分形式:
${∫f(x)g(x)dx}^2≤∫f^2(x)dx∫g^2(x)dx$
概率论形式:
$\sqrt{E(X^2)\sqrt{E(Y^2)}
-----没事了是水军太多搞爆了
