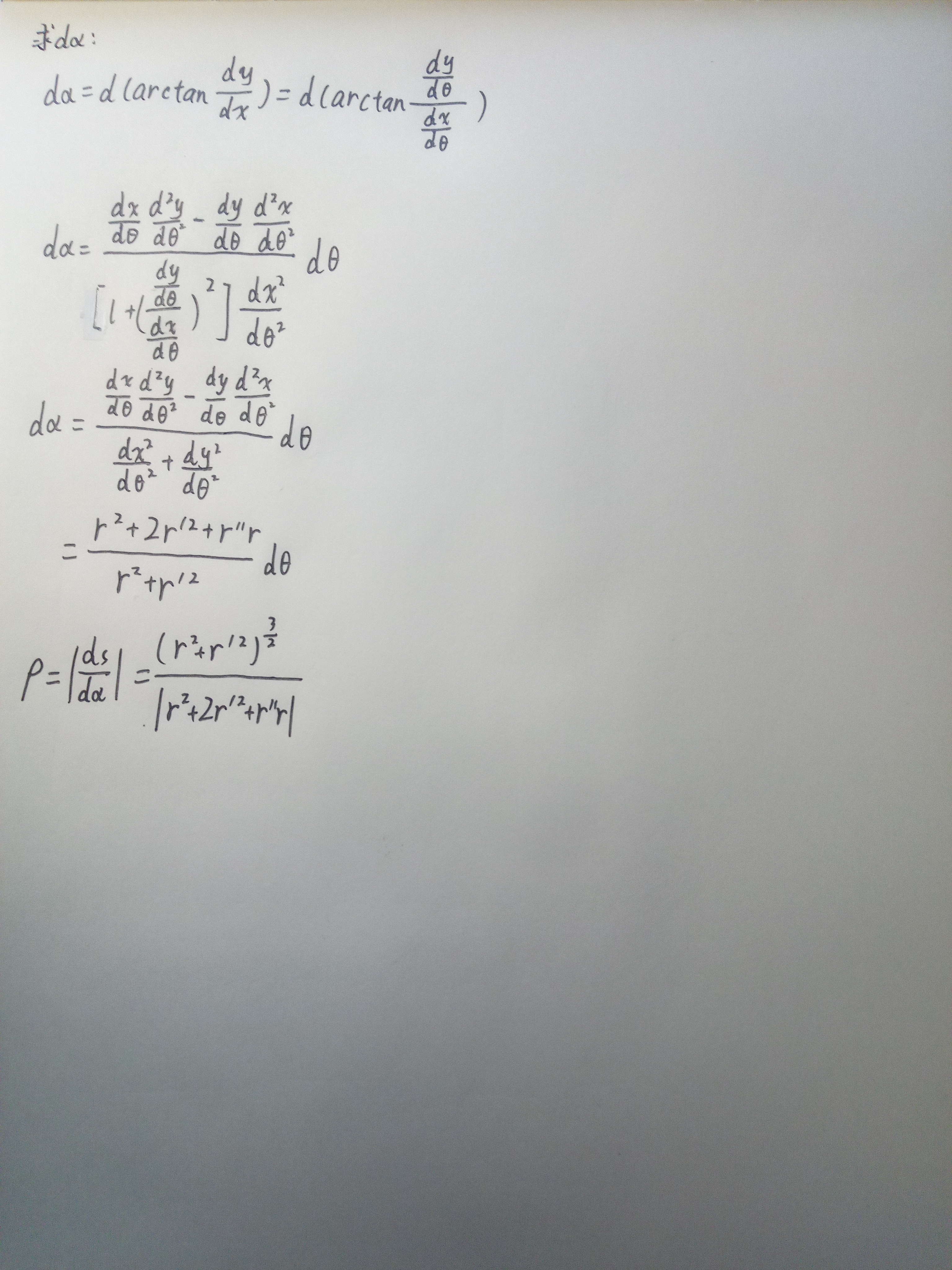（共四题，预赛难度）

Level 1 做题人数统计（截至2024/9）：共9人参与做题，第一题（爆算三角函数）6人，第二题（空间追及问题）2人，第三题（最远飞行距离）4人，第四题（求解曲率半径）4人

Level 1 做题建议：独立完成，将解题过程发在评论区（注意这里是Level 1，不要发错了），最好注明用时，最好再反馈一下难度

Level 1 题目评价：主要考查运动学基础知识和基本能力；第一题考查三角函数公式和运算技巧；第二题创新性较强，结合立体几何与高阶小量考查追及问题，难度较大；第三题考查相对运动和审题能力；第四题考查极坐标系，还设置了“验算”环节，你可以根据你做题的确定性和时间来选择是否验算

第一题 爆算三角函数（40分）

如图，倾角为θ的斜面的上方有一点P，到斜面的竖直高度为h，斜面上有一动点Q，沿PQ设置一斜面，使物块从P下滑到Q，设PQ与竖直方向的夹角为α（α≥0），物块从P下滑到Q用时为t

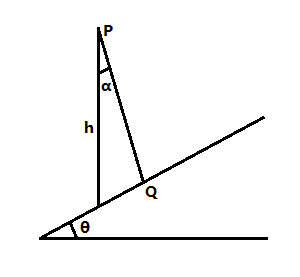
(1)（14分）若PQ光滑，物块初速度为0，要使t最小，求α和t

(2)（14分）若PQ动摩擦因数为μ，物块初速度为0，要使t最小，求α和t

(3)（12分）若PQ动摩擦因数为μ，物块初速度为$v_0$，h未知，已知当t最小时对应的角度为α（α>0），求t(α)和h(α)

第二题 空间追及问题（40分）

如图，4个质点初始位置构成棱长为$l_0$的正四面体（质点3在xy平面内），1追2，2追3，3追4，4追1，速率v恒定（速度方向始终指向被追的质点）

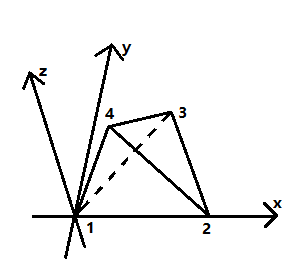
(1)（10分）求初始时刻1,2间距离的变化率和1,3间距离的变化率，判断4个质点的相对位置能否保持正四面体

(2)（14分）求初始时刻1的加速度和2相对1的加速度（用x,y,z分量表示，下同）

(3)（16分）求初始时刻1的加速度的变化率（提示：将dt时间内质点的轨迹近似为抛物线）

参考公式：$\dfrac{1}{\sqrt{A+B\mathrm{d}t+C\mathrm{d}t^2}}=\dfrac{1}{\sqrt{A}}[1-\dfrac{B}{2A}\mathrm{d}t+(\dfrac{3B^2}{8A^2}-\dfrac{C}{2A})\mathrm{d}t^2]$

第三题 最远飞行距离（40分）

一架飞机在无风时以匀速v相对地面飞行，由于飞机能量有限，最远飞行距离（飞机相对地面的路程的上限）为R。现飞机在风速为u，方向为北偏东α角的风中飞行（相对风的速度仍为v），从原点沿直线向北偏东β角方向飞出一段距离再原路飞回原点，u<v，0<α,β<90°

(1)（10分）若α=β，求此种情况下的最远飞行距离

(2)（12分）若α≠β，求此种情况下的飞机飞出时相对风的速度方向（用北偏东的角度表示）和飞回时相对风的速度方向（用南偏西的角度表示）

(3)（18分）若α≠β，求此种情况下的最远飞行距离

第四题 求解曲率半径（40分）

(1)（10分）在直角坐标系中，曲线方程能用函数$y=y(x)$表示，用运动学方法求曲线上任一点的曲率半径（用$y'(x),y''(x)$表示）

(2)（15分）在极坐标系中，曲线方程能用函数$r=r(θ)$表示，用运动学方法求曲线上任一点的曲率半径（用$r(θ),r'(θ),r''(θ)$表示）

(3)（15分）在极坐标系中，曲线方程能用函数$θ=θ(r)$表示，用运动学方法求曲线上任一点的曲率半径（用$r,θ'(r),θ''(r)$表示）

提示：抛物线$y=\dfrac{x^2}{4}-1$在极坐标系中是$r=\dfrac{2}{1-\sinθ}$，你可以用它来验算

$\color{red}答案解析$

还没做题的不要往下翻！

第一题 爆算三角函数（40分）

(1)（14分）

根据几何关系，得

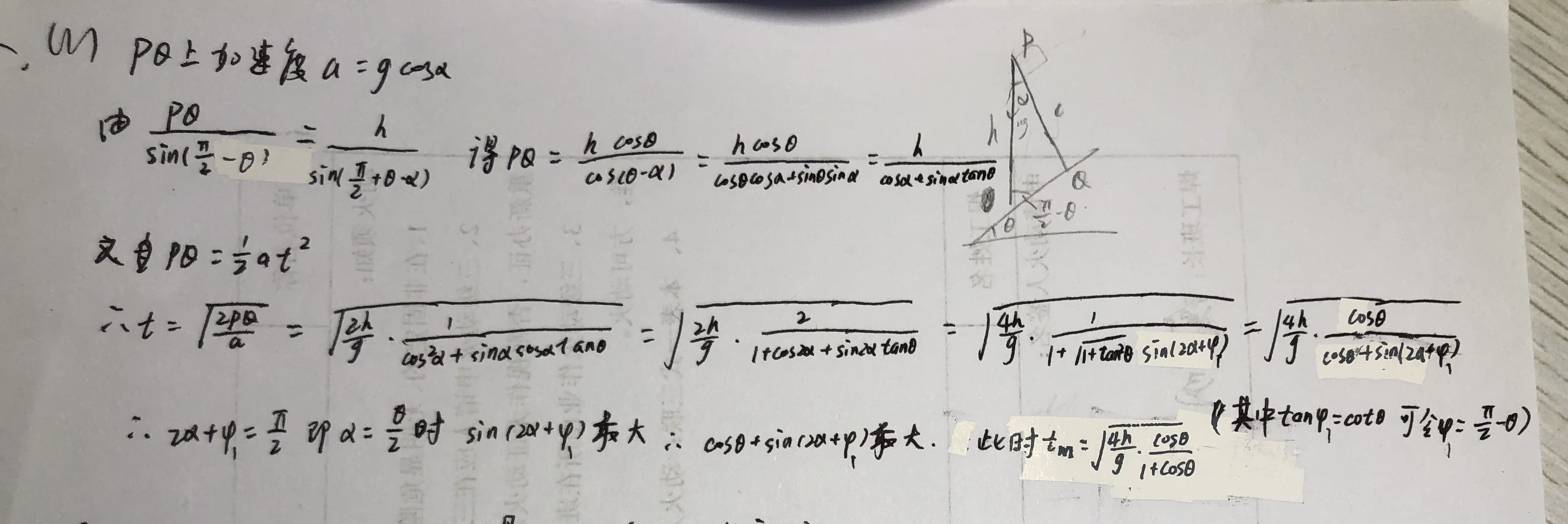
$l=\dfrac{h\cos\theta}{\cos(\theta-\alpha)}$  （2分）

$a=g\cos\alpha$  （2分）

根据运动学公式，得

$t=\sqrt{\dfrac{2l}{a}}$  （2分）

代入，得

$t=\sqrt{\dfrac{2h\cos\theta}{g\cos\alpha\cos(\theta-\alpha)}}$  （2分）

利用三角函数公式化简，得

$t=\sqrt{\dfrac{2h\cos\theta}{g[\cos\theta+\cos(2\alpha-\theta)]}}$  （2分）

解得

$\alpha=\dfrac{\theta}{2}$  （2分）

$t=\sqrt{\dfrac{2h\cos\theta}{g(\cos\theta+1)}}$  （2分）

(2)（14分）

根据牛顿第二定律，得

$a=g(\cos\alpha-\mu\sin\alpha)$  （2分）

利用三角函数公式化简，得

$a=g\sqrt{\mu^2+1}\cos(\alpha+\varphi)$，其中$\varphi=\arctan\mu$  （2分）

同(1)的方法，得

$t=\sqrt{\dfrac{2h\cos\theta}{g\sqrt{\mu^2+1}\cos(\alpha+\varphi)\cos(\theta-\alpha)}}$  （2分）

$t=\sqrt{\dfrac{2h\cos\theta}{g\sqrt{\mu^2+1}[\cos(\theta+\varphi)+\cos(2\alpha+\varphi-\theta)]}}$  （2分）

讨论：

(i)  $\varphi\ge\theta$

解得

$\alpha=0$  （1分）

$t=\sqrt{\dfrac{2h}{g}}$  （1分）

(ii)  $\varphi<\theta$

解得

$\alpha=\dfrac{\theta-\varphi}{2}=\dfrac{\theta-\arctan\mu}{2}$  （2分）

$t=\sqrt{\dfrac{2h\cos\theta}{g\sqrt{\mu^2+1}[\cos(\theta+\varphi)+1]}}=\sqrt{\dfrac{2h\cos\theta}{g(\cos\theta-\mu\sin\theta+\sqrt{\mu^2+1})}}$  （2分）

(3)（12分）

根据运动学公式，得

$l=v_0t+\frac{1}{2}at^2$  （2分）

代入，得

$h\cos\theta=v_0t\cos(\theta-\alpha)+\frac{1}{2}gt^2(\cos\alpha-\mu\sin\alpha)\cos(\theta-\alpha)$  （2分）（*）

（*）式是关于h,t,α的隐函数，因为在h不变的前提下t最小，所以α小幅变化时，h和t都不变

两边对α求导

$0=v_0t\sin(\theta-\alpha)-\frac{1}{2}gt^2[\sin(2\alpha-\theta)+\mu\cos(2\alpha-\theta)]$  （2分）

解得

$t(\alpha)=\dfrac{2v_0\sin(\theta-\alpha)}{g[\sin(2\alpha-\theta)+\mu\cos(2\alpha-\theta)]}$  （3分）

代入（*）式，得

$h(\alpha)=\dfrac{1}{\cos\theta}[\dfrac{2v_0^2\sin(\theta-\alpha)\cos(\theta-\alpha)}{g[\sin(2\alpha-\theta)+\mu\cos(2\alpha-\theta)]}+\dfrac{2v_0^2\sin^2(\theta-\alpha)\cos(\theta-\alpha)}{g[\sin(2\alpha-\theta)+\mu\cos(2\alpha-\theta)]^2}(\cos\alpha-\mu\sin\alpha)]$  （3分）

第二题 空间追及问题（40分）

(1)（10分）

距离的变化率就是相对速度

质点1沿12方向的速度  $v_{12}=v$  （1分）

质点2沿21方向的速度  $v_{21}=v\cos60°$  （1分）

质点1,2的相对速度  $v'_{12}=v_{12}+v_{21}=\frac{3}{2}v$  （2分）

质点1沿13方向的速度  $v_{13}=v\cos60°$  （1分）

质点3沿31方向的速度  $v_{31}=v\cos60°$  （1分）

质点1,3的相对速度  $v'_{13}=v_{13}+v_{31}=v$  （2分）

因为距离的变化率不相等，所以一段时间后1,2的距离与1,3不相等，相对位置不能保持正四面体  （2分）

(2)（14分）

dt时间内，1,2连线角度的变化，即质点1速度方向的变化  $\mathrm{d}\theta=\dfrac{v\mathrm{d}t\sin60°}{r}$  （2分）

质点1速度大小不变，dt时间内，方向在xy平面内变化（z方向的速度变化为高阶小量）

$a_{1x}=0$  （1分）

$a_{1y}=\dfrac{v\mathrm{d}\theta}{\mathrm{d}t}=\dfrac{\sqrt3v^2}{2r}$  （2分）

$a_{1z}=0$  （1分）

质点2加速度大小与1相等，方向由几何关系求出

$a_{2x}=-\dfrac{\sqrt3}{6}a_1=-\dfrac{v^2}{4r}$  （1分）

$a_{2y}=-\dfrac{1}{6}a_1=-\dfrac{\sqrt3v^2}{12r}$  （1分）

$a_{2z}=\dfrac{2\sqrt2}{3}a_1=\dfrac{\sqrt6v^2}{3r}$  （1分）

2相对1的加速度  $\vec{a'}=\vec{a_2}-\vec{a_1}$  （2分）

$a'_{x}=-\dfrac{v^2}{4r}$  （1分）

$a'_{y}=-\dfrac{7\sqrt3v^2}{12r}$  （1分）

$a'_{z}=\dfrac{\sqrt6v^2}{3r}$  （1分）

(3)（16分）

保留二阶小量，根据运动学公式，得dt时间后2相对1的位置

$\vec{r'}=\vec{r'_0}+\vec{v'_0}\mathrm{d}t+\frac{1}{2}\vec{a'}\mathrm{d}t^2$  （2分）

由初始条件，得

$\begin{cases}\vec{r'_0}=(r,0,0)\\\vec{v'_0}=(\frac{3}{2}v,0,0)\end{cases}$  （1分）

$\vec{a'}$已在(2)中求出

代入，得

$\vec{r'}=(r-\dfrac{3}{2}v\mathrm{d}t-\dfrac{v^2}{8r}\mathrm{d}t^2,\dfrac{\sqrt3}{2}v\mathrm{d}t-\dfrac{7\sqrt3v^2}{24r}\mathrm{d}t^2,\dfrac{\sqrt6v^2}{6r}\mathrm{d}t^2)$  （3分）

$|\vec{r'}|=\sqrt{r^2-3rv\mathrm{d}t+\dfrac{11v^2}{4}\mathrm{d}t^2}$  （1分）

$\dfrac{1}{|\vec{r'}|}=\dfrac{1}{r}+\dfrac{3v}{2r^2}\mathrm{d}t+\dfrac{2v^2}{r^3}\mathrm{d}t^2$  （1分）

dt时间后1的速度 $v_1(\mathrm{d}t)$ 为

$v_{1x}=\dfrac{r'_x}{|\vec{r'}|}v=v-\dfrac{3v^3}{8r^2}\mathrm{d}t^2$  （1分）

$v_{1y}=\dfrac{r'_y}{|\vec{r'}|}v=\dfrac{\sqrt3v^2}{2r}\mathrm{d}t+\dfrac{11\sqrt3v^3}{24r^2}\mathrm{d}t^2$  （1分）

$v_{1z}=\dfrac{r'_z}{|\vec{r'}|}v=\dfrac{\sqrt6v^3}{6r^2}\mathrm{d}t^2$  （1分）

根据运动学公式，得

$\dfrac{\mathrm{d}\vec{a_1}}{\mathrm{d}t}=\dfrac{\mathrm{d}^2\vec{v_1}(t)}{\mathrm{d}t^2}$  （2分）

解得

$\dfrac{\mathrm{d}\vec{a_{1x}}}{\mathrm{d}t}=-\dfrac{3v^3}{4r^2}$  （1分）

$\dfrac{\mathrm{d}\vec{a_{1y}}}{\mathrm{d}t}=\dfrac{11\sqrt3v^3}{12r^2}$  （1分）

$\dfrac{\mathrm{d}\vec{a_{1z}}}{\mathrm{d}t}=\dfrac{\sqrt6v^3}{3r^2}$  （1分）

第三题 最远飞行距离（40分）

(1)（10分）

由题意，得最远飞行时间  $t=\dfrac{R}{v}$  （2分）

设α=β时最远飞行距离为$r_1$ （注意“最远飞行距离”是飞出再飞回的路程）

飞出：  $t_1=\dfrac{\frac{r_1}{2}}{v+u}$  （3分）

飞回：  $t_2=\dfrac{\frac{r_1}{2}}{v-u}$  （3分）

$t=t_1+t_2$

解得  $r_1=\dfrac{v^2-u^2}{v^2}R$  （2分）

(2)（12分）

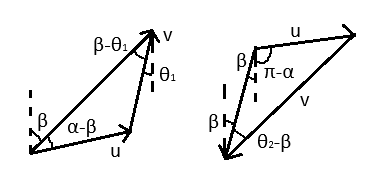
作矢量分析图（α>β），由正弦定理，得

飞出：  $\dfrac{v}{\sin(\alpha-\beta)}=\dfrac{u}{\sin(\beta-\theta_1)}$  （3分）

飞回：  $\dfrac{v}{\sin(\pi-\alpha+\beta)}=\dfrac{u}{\sin(\theta_2-\beta)}$  （3分）

以上两式在α<β时也正确  （2分）

（注意arcsin的值域为$[-\frac{\pi}{2},\frac{\pi}{2}]$，由题给条件得$\beta-\theta_1$和$\theta_2-\beta$的取值范围为$(-\frac{\pi}{2},\frac{\pi}{2})$，可以直接用arcsin表示结果）

解得

飞出：  $\theta_1=\beta-\arcsin[\dfrac{u}{v}\sin(\alpha-\beta)]$  （2分）

飞回：  $\theta_2=\beta+\arcsin[\dfrac{u}{v}\sin(\alpha-\beta)]$  （2分）

(3)（18分）

先求飞机相对地面的速度，根据矢量分析图（α>β），由余弦定理，得

飞出：  $v^2=v_1^2+u^2-2v_1u\cos(\alpha-\beta)$  （2分）

飞回：  $v^2=v_2^2+u^2-2v_1u\cos(\pi-\alpha+\beta)$  （2分）

以上两式在α<β时也正确

解得（负值舍去）

飞出：  $v_1=u\cos(\alpha-\beta)+\sqrt{v^2-u^2\sin^2(\alpha-\beta)}$  （2分）

飞回：  $v_2=-u\cos(\alpha-\beta)+\sqrt{v^2-u^2\sin^2(\alpha-\beta)}$  （2分）

设最远飞行距离为$r$ （注意“最远飞行距离”是飞出再飞回的路程）

飞出：  $t_1=\dfrac{\frac{r}{2}}{v_1}$  （2分）

飞回：  $t_2=\dfrac{\frac{r}{2}}{v_2}$  （2分）

$t=t_1+t_2$

解得  $r=\dfrac{(v^2-u^2)R}{v\sqrt{v^2-u^2\sin^2(\alpha-\beta)}}$  （6分）

第四题 求解曲率半径（40分）

(1)（10分）

设质点沿曲线y(x)运动，在x方向上的分速度$v_x=\dfrac{\mathrm{d}x}{\mathrm{d}t}$不变  （1分）

$v_y=\dfrac{\mathrm{d}y}{\mathrm{d}t}=\dfrac{\mathrm{d}y}{\mathrm{d}x}\cdot\dfrac{\mathrm{d}x}{\mathrm{d}t}=y'(x)v_x$  （1分）

$v=\sqrt{v_x^2+v_y^2}=\sqrt{1+y'^2(x)}v_x$  （1分）

设速度方向与x轴的夹角为$φ$

$\cos\varphi=\dfrac{v_x}{v}=\dfrac{1}{\sqrt{1+y'^2(x)}}$

$a_y=\dfrac{\mathrm{d}v_y}{\mathrm{d}t}=\dfrac{\mathrm{d}v_y}{\mathrm{d}x}v_x=y''(x)v_x^2$  （2分）（*）

$|a_n|=|a_y\cos\varphi|=\dfrac{|y''(x)|v_x^2}{\sqrt{1+y'^2(x)}}$  （1分）

曲率半径公式  $\rho=\dfrac{v^2}{|a_n|}$  （2分）

解得  $\rho=\dfrac{(1+y'^2(x))^{3/2}}{|y''(x)|}$  （2分）

（注意：由（*）式得$\dfrac{\mathrm{d}^2y}{\mathrm{d}t^2}=\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\cdot(\dfrac{\mathrm{d}x}{\mathrm{d}t})^2$，这一结论只在$\dfrac{\mathrm{d}x}{\mathrm{d}t}$不变的前提下成立，后两问会用到这一结论）

(2)（15分）

设质点沿曲线r(θ)运动，在θ方向上的分速度$v_θ=\dfrac{r(θ)\mathrm{d}θ}{\mathrm{d}t}$不变  （1分）

$v_r=\dfrac{\mathrm{d}r}{\mathrm{d}t}=\dfrac{\mathrm{d}r}{\mathrm{d}θ}\cdot\dfrac{\mathrm{d}θ}{\mathrm{d}t}=\dfrac{r'(θ)}{r(θ)}v_θ$  （2分）

$v=\sqrt{v_r^2+v_θ^2}=\sqrt{1+(\frac{r'(θ)}{r(θ)})^2}v_θ$  （1分）

设速度方向与r轴的夹角为$φ$

$\sin\varphi=\dfrac{v_θ}{v}=\dfrac{1}{\sqrt{1+(\frac{r'(θ)}{r(θ)})^2}}$

根据极坐标系公式

$a_r=\ddot{r}-r\dot{\theta}^2$  （1分）

$a_\theta=2\dot{r}\dot{\theta}+r\ddot{\theta}$  （1分）

代入，得

$a_r=\dfrac{r''(θ)}{r^2(θ)}v_\theta^2-\dfrac{v_\theta^2}{r(θ)}$  （2分）

$a_\theta=\dfrac{2r'(θ)}{r^2(θ)}v_\theta^2$  （2分）

$|a_n|=|a_\theta\cos\varphi-a_r\sin\varphi|=\dfrac{v_\theta^2}{\sqrt{1+(\frac{r'(θ)}{r(θ)})^2}}|\dfrac{2r'^2(θ)}{r^3(θ)}-\dfrac{r''(θ)}{r^2(θ)}+\dfrac{1}{r(θ)}|$  （2分）

曲率半径公式  $\rho=\dfrac{v^2}{|a_n|}$

解得  $\rho=\dfrac{(r^2(θ)+r'^2(θ))^{3/2}}{|r''(θ)r(θ)-r^2(θ)-2r'^2(θ)|}$  （3分）

(3)（15分）

设质点沿曲线θ(r)运动，在r方向上的分速度$v_r=\dfrac{\mathrm{d}r}{\mathrm{d}t}$不变  （1分）

$v_θ=\dfrac{r\mathrm{d}θ}{\mathrm{d}t}=rθ'(r)v_r$  （2分）

$v=\sqrt{v_r^2+v_θ^2}=\sqrt{1+r^2θ'^2(r)}v_r$  （1分）

设速度方向与r轴的夹角为$φ$

$\cos\varphi=\dfrac{v_r}{v}=\dfrac{1}{\sqrt{1+r^2θ'^2(r)}}$

根据极坐标系公式

$a_r=\ddot{r}-r\dot{\theta}^2$  （1分）

$a_\theta=2\dot{r}\dot{\theta}+r\ddot{\theta}$  （1分）

代入，得

$a_r=-rθ'^2(r)v_r^2$  （2分）

$a_\theta=2θ'(r)v_r^2+rθ''(r)v_r^2$  （2分）

$|a_n|=|a_\theta\cos\varphi-a_r\sin\varphi|=\dfrac{v_r^2}{\sqrt{1+r^2θ'^2(r)}}|2θ'(r)+rθ''(r)+r^2θ'^3(r)|$  （2分）

曲率半径公式  $\rho=\dfrac{v^2}{|a_n|}$

解得  $\rho=\dfrac{(1+r^2θ'^2(r))^{3/2}}{|2θ'(r)+rθ''(r)+r^2θ'^3(r)|}$  （3分）