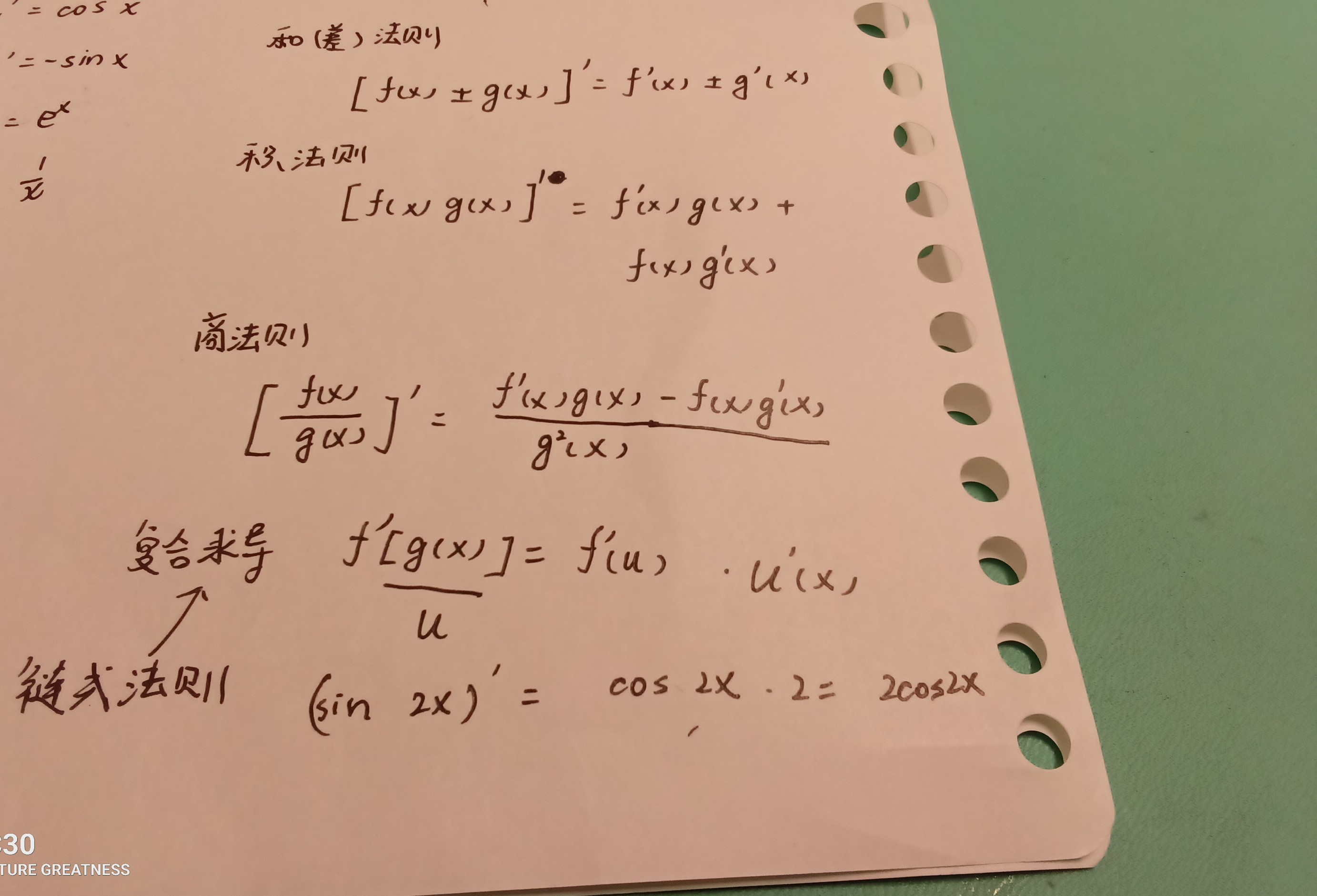物理

『栖岸计划』再谈导数------物理学下的高等数学(基础)

“周而复始，不休”

在高一物理之中，我们都学过瞬时速度与平均速度。平均速度用vt图像非常好表示。

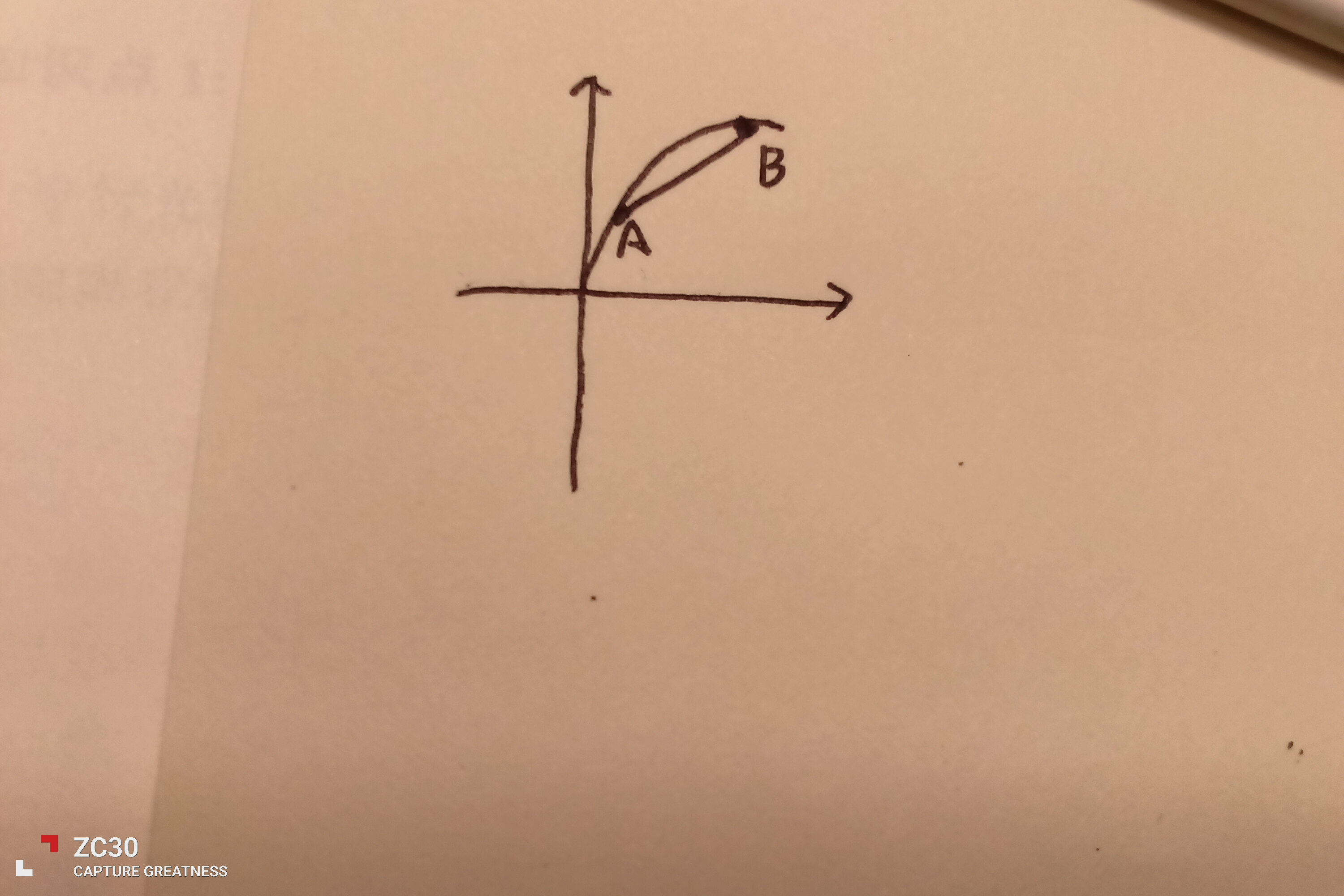
以上是平均速度的表示，即直线AB的斜率k，kAB。

那么瞬时速度呢？这里要提到一个旧的概念，切线。对，切线。那么有同学提出了问题：切线不是在圆才有的吗？而且曲线的运动轨迹也不是标准的圆弧啊。是的，但曲线与坐标轴上的某一条直线有且仅有一个交点的时候，我们定义其为曲线切线。好了，我们已经发现了导数。导数就是这条切线的斜率。

对于导数，给出如下标准定义：

曲线切线，过曲线$y=f(x)$上一点p做曲线的割线PQ，当Q沿着曲线无限趋近与p时，若割线PQ趋近于某一确定的直线PT，则这一确定的直线PT成为曲线$y=f(x)$在点P的切线。导数几何意义：函数$y=f(x)$，在$x=x_0$处的导数，就是曲线$y=f(x)$在$x=x_0$处切线的斜率。

即$k=\lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = f'(x_0) $，相应切线方程为$y-f(x_0)=f'(x_0)(x-x_0)$

那么让我们来看一道练习吧(别问题从哪来的)

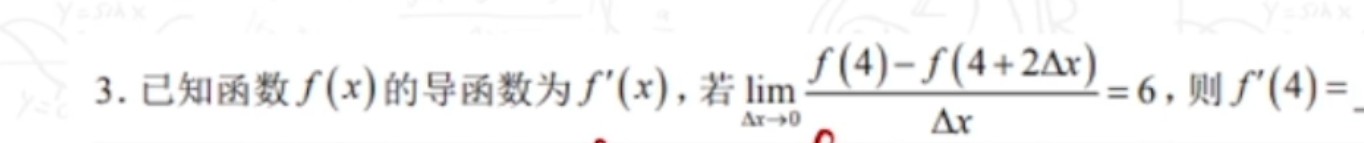
看到题目后，对于一个导数初学者，自然不会做。这也套不了导数的公式啊！注意到导数的分子式左边有一个$\Delta x$，而右边没有，左式减去右式，正好剩下一个$\Delta x$，与分母上的一个$\Delta x$相约分。但此题左式没有$\Delta x$，右边有2个，共有0-(+2)=-2个$\Delta x$，并不能与分母约分。那我们将原式变成如下图

学完了什么是导数，那么如何求导呢。

这里给出几种常见的求导法则。

1.公式法，除背诵外别无他法。

2. 差、积、商法则

 差法则（导数的线性性质）：

$\( \frac{d}{dx}[f(x) - g(x)] = f'(x) - g'(x) \)$

和法则：

$\( \frac{d}{dx}[f(x) + g(x)] = f'(x) + g'(x) \)$

乘积法则：

$\[ \frac{d}{dx}[f(x)g(x)] = f'(x)g(x) + f(x)g'(x) \]$   或写成：$\( (fg)' = f'g + fg' \)$

商法则：

$\[ \frac{d}{dx}\left[\frac{f(x)}{g(x)}\right] = \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2} \]$

或写成：$\( \left(\frac{f}{g}\right)' = \frac{f'g - fg'}{g^2} \)$

3. 链式法则

用于复合函数的求导。若$ \( y = f(g(x)) \)$，则：$\[ \frac{dy}{dx} = f'(g(x)) \cdot g'(x) \]$

或写成：$\( \frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x) \)$

也可以用莱布尼茨记号表示为：$\[ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} \quad \text{其中 } u = g(x),\ y = f(u) \]$