数学 [栖岸计划] 熟悉而又陌生的朋友——π
本帖归属于[栖岸计划]
本帖是一个拓展类帖子,能够让大家更深入的了解圆周率以及圆周率在数学中的重要地位
适用人群:竞赛一轮+
emmmm,我觉得过年前我的事情有点多,估计要五天一更,更在评论区
本帖禁止开楼,有疑问可以去疑问楼指出,谢谢各位
正文:
关于圆周率$π$,这可是一个家喻户晓的名词。
一.小引(几何方面的认识)
$π$,在幼儿园我们学过,表示周长与直径的比值,即$π=\frac{C}{d}$,也可以用半径r表示,即$π=\frac{C}{2r}$,他也和圆面积有关系,也就是我们幼儿园学过的$A=π r^2$
比如:
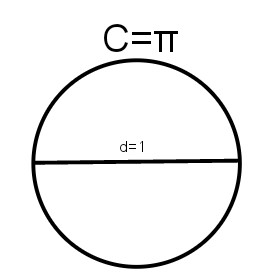 这时,一个美味的$π$就出现了
这时,一个美味的$π$就出现了二.如何证明$π$是无理数?
在回顾完幼儿园知识后,我们是不是想起一些东西,$π$是无理数还是有理数呢?相信屏幕前的你一定一毫秒就反应过来是无理数,那么豪,我们要如何证明$π$是无理数呢?
在我们学到$π$的时候,本好学宝宝问老师:“唉老师老师,这个$π$为啥是无理数啊?”老师告诉我,这个问题你要上大学才能得到答案。
哦吼~
目前有两种较常见解法,一种是Lambert使用的正切函数,另一种是Niven利用一个魔法函数加积分的方式。现在比较流行的是Niven的证法
二.1 Lambert的证法,见评论区
补充:Lambert的证法主要依赖于一个定理,即非零有理数的正切值一定为无理数,才能解决此问题。所以我将证明方法和此定理分开编写
二.2 Niven的证法,见评论区+1
其他证明方法也可以告诉我,从而增加这件事情的趣味😋😋😋
那么既然证明出$π$是无理数了,那主包顺便证一下$π$是超越数吧🤗🤗🤗。证明完$π$是无理数,这件事其实就是顺水推舟
二.3 $π$是超越数的证明,见评论区
在不懈努力下,我们证明了$π$是无理数和超越数。呼,最“有趣”的事情我们解决完了,接下来就是一些站在巨人肩膀上的东西了
三.$π$的表示方法
四.$π$的各种用途
共2条回复
时间正序
