物理

三角函数公式

本帖用作总结和$LaTeX$练习

(新加了一些公式之后越来越没条理了)

$\sin A + \sin B = 2 \sin\left(\frac{A+B}{2}\right) \cos\left(\frac{A-B}{2}\right)$

$\sin A - \sin B = 2 \cos\left(\frac{A+B}{2}\right) \sin\left(\frac{A-B}{2}\right)$

$\cos A + \cos B = 2 \cos\left(\frac{A+B}{2}\right) \cos\left(\frac{A-B}{2}\right)$

$\cos A - \cos B = -2 \sin\left(\frac{A+B}{2}\right) \sin\left(\frac{A-B}{2}\right)$

$\sin A \sin B = \frac{1}{2} [\cos(A-B) - \cos(A+B)]$

$\cos A \cos B = \frac{1}{2} [\cos(A-B) + \cos(A+B)]$

$\sin A \cos B = \frac{1}{2} [\sin(A+B) + \sin(A-B)]$

万能公式

 $ t = \tan\left(\frac{x}{2}\right) $，

$\sin x = \frac{2t}{1+t^2}, \quad \cos x = \frac{1-t^2}{1+t^2}, \quad \tan x = \frac{2t}{1-t^2}$

辅角公式

$a \sin x + b \cos x = \sqrt{a^2 + b^2} \sin(x + \varphi)$

其中 $ \varphi = \arctan\left(\frac{b}{a}\right) $

三倍角公式

$\sin 3x = 3 \sin x - 4 \sin^3 x$

$\cos 3x = 4 \cos^3 x - 3 \cos x$

$\tan 3x = \frac{3 \tan x - \tan^3 x}{1 - 3 \tan^2 x}$

$\tan 4x = \frac{4 \tan x - 4 \tan^3 x}{1 - 6 \tan^2 x + \tan^4 x}$

半角公式

$\sin\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 - \cos x}{2}}, \quad \cos\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 + \cos x}{2}}$

平方

$\sin^2 x + \cos^2 x = 1$

$1 + \tan^2 x = \sec^2 x$

$1 + \cot^2 x = \csc^2 x$

降幂公式

$\sin^2 x = \frac{1 - \cos 2x}{2}, \quad \cos^2 x = \frac{1 + \cos 2x}{2}$

和角公式

$\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B$

$\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B$

$\tan(A \pm B) = \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$

$\sin(A+B+C) = \sin A \cos B \cos C + \cos A \sin B \cos C + \cos A \cos B \sin C - \sin A \sin B \sin C$

不等式

$|\sin x| \leq 1, \quad |\cos x| \leq 1$

$Jensen$ 不等式应用（凸函数）

如：在 $ (0, \pi) $ 上

$\frac{\sin A + \sin B + \sin C}{3} \leq \sin\left(\frac{A+B+C}{3}\right) = \sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}$

当且仅当 $ A = B = C = \frac{\pi}{3} $ 取等。

若 $ A + B + C = \pi $，则：

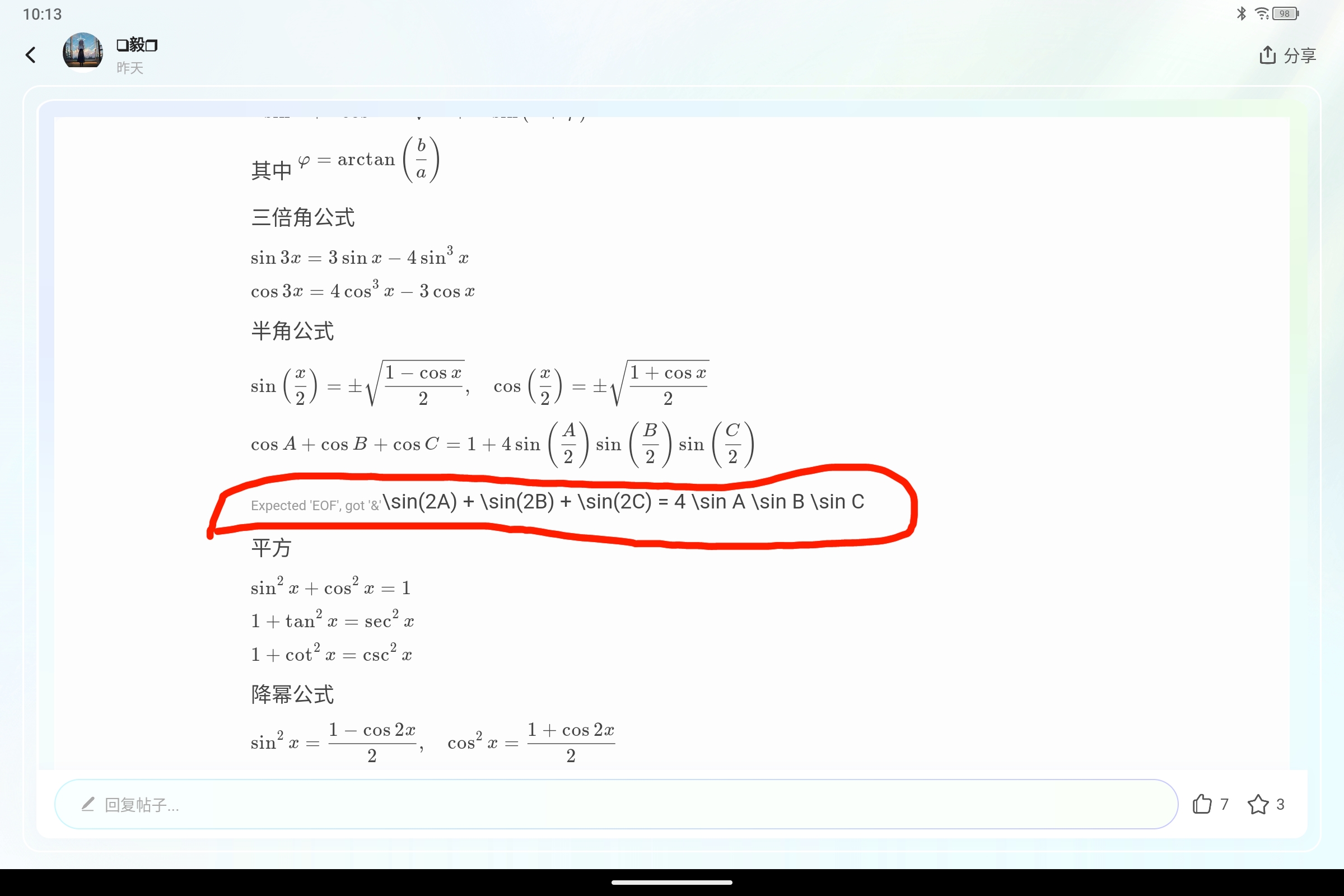
$\sin(2A) + \sin(2B) + \sin(2C) = 4 \sin A \sin B \sin C$

$\cos^2 A + \cos^2 B + \cos^2 C + 2 \cos A \cos B \cos C = 1$

$\tan A + \tan B + \tan C = \tan A \tan B \tan C$

进一步

$\tan^2 A + \tan^2 B + \tan^2 C = \tan^2 A \tan^2 B \tan^2 C - 2(\tan A \tan B + \tan B \tan C + \tan C \tan A)$

$\tan\left(\frac{A}{2}\right)\tan\left(\frac{B}{2}\right) + \tan\left(\frac{B}{2}\right)\tan\left(\frac{C}{2}\right) + \tan\left(\frac{C}{2}\right)\tan\left(\frac{A}{2}\right) = 1$

$\sin A + \sin B + \sin C = 4 \cos\left(\frac{A}{2}\right)\cos\left(\frac{B}{2}\right)\cos\left(\frac{C}{2}\right)$

$\cos A + \cos B + \cos C = 1 + \frac{r}{R}$

$\frac{1}{\sin A} + \frac{1}{\sin B} + \frac{1}{\sin C} \geq \frac{6}{\sqrt{3}} = 2\sqrt{3}$

当且仅当 $ A = B = C = \frac{\pi}{3} $ 取等

连乘积

对于任意整数 $ n \geq 1 $，有：

$\prod_{k=1}^{n-1} \sin\left(\frac{k\pi}{n}\right) = \frac{n}{2^{n-1}}$

如：

$\sin\left(\frac{\pi}{5}\right)\sin\left(\frac{2\pi}{5}\right)\sin\left(\frac{3\pi}{5}\right)\sin\left(\frac{4\pi}{5}\right) = \frac{5}{16}$

$\prod_{k=1}^{n-1} \cos\left(\frac{k\pi}{2n}\right) = \frac{\sqrt{n}}{2^{n-1}}$

反三角函数

$\arctan a + \arctan b = \arctan\left( \frac{a + b}{1 - ab} \right) \quad$,当ab<1时

$\arctan 1 + \arctan 2 + \arctan 3 = \pi$

$\arctan x + \arctan \frac{1}{x} = \frac{\pi}{2}, \quad $(x > 0)

高级

傅里叶级数或无穷乘积

$\sin \pi x = \pi x \prod_{n=1}^{\infty} \left(1 - \frac{x^2}{n^2}\right)$

欧拉公式推广：

$\sum_{k=1}^{n} \sin(kx) = \frac{\sin\left(\frac{nx}{2}\right) \cdot \sin\left(\frac{(n+1)x}{2}\right)}{\sin\left(\frac{x}{2}\right)}$

用于求和

复数代换

令 $ z = e^{ix} $，则：

$\sin x = \frac{z - z^{-1}}{2i}, \quad \cos x = \frac{z + z^{-1}}{2}$