物理

几何最值-阿氏圆

$\tiny{讲的不是很好，仅限初中范围}$

阿氏圆是一类最值问题，会出现在填空题16题的位置，但是中考基本上不会涉及，因为这类问题属于是知道就秒出，不知道就怎么也做不出来的那种

不过知道还是有好处的（（

下面我们来学学阿氏圆

$\large{基本图形}$

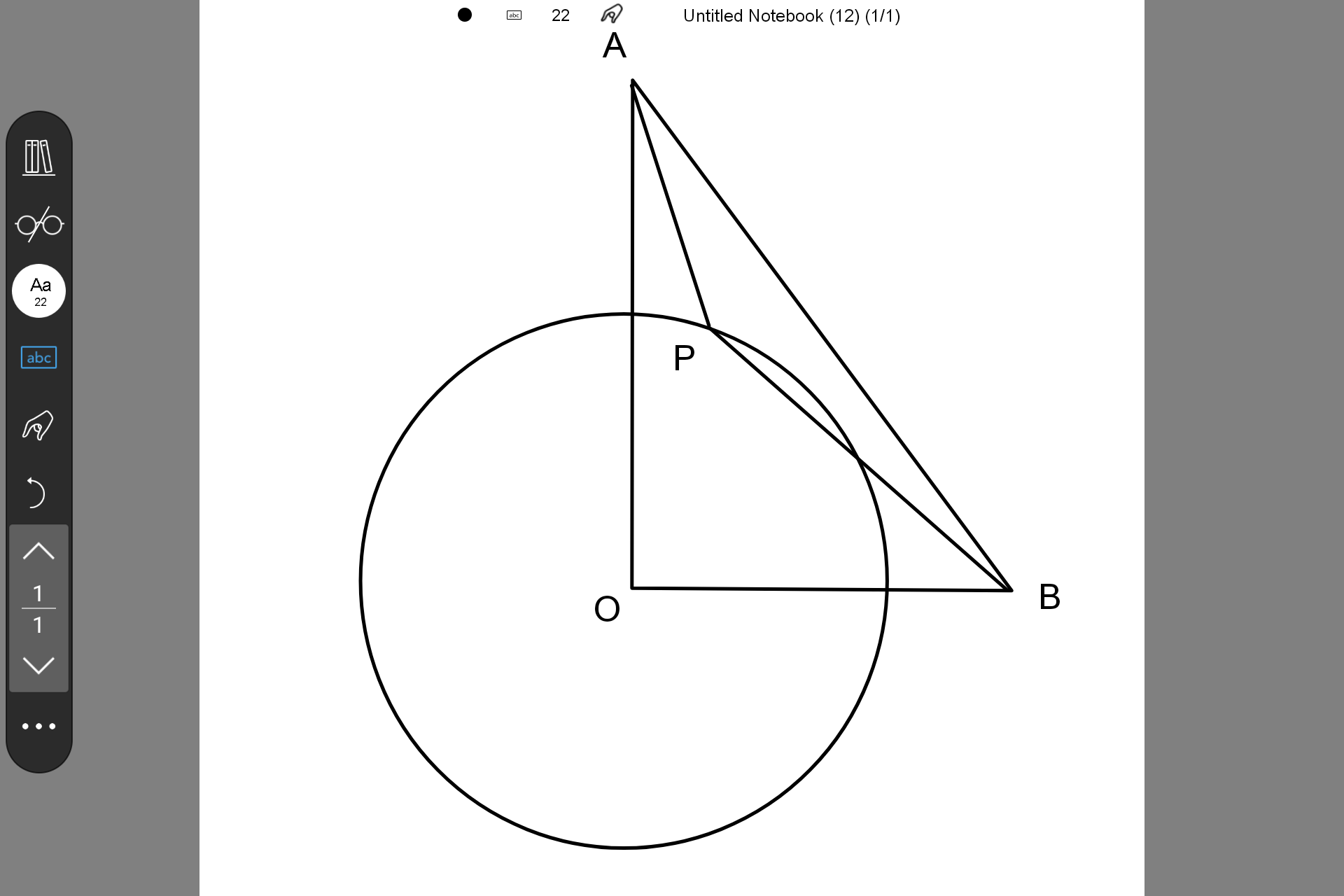
（大部分）一个圆（比如$\odot O$）加一个直角三角形（比如$\triangle ABO$），圆上有任意一点$P$，求$kAP＋BP$的最小值

$\large{基本原理}$

构造相似比为$1:k$的相似三角形，将$kAP$转化，后用两点之间线段最短解决

这么讲还是有点抽象，下面看例题

$\large{例题}$

如图，$\triangle ABO$为等腰直角三角形，$AO=BO=2$，作$\odot O 与AB相切$，$\angle O=90^\circ$，$P$为圆上任意一点，求$\sqrt{2}AP＋BP$最小值

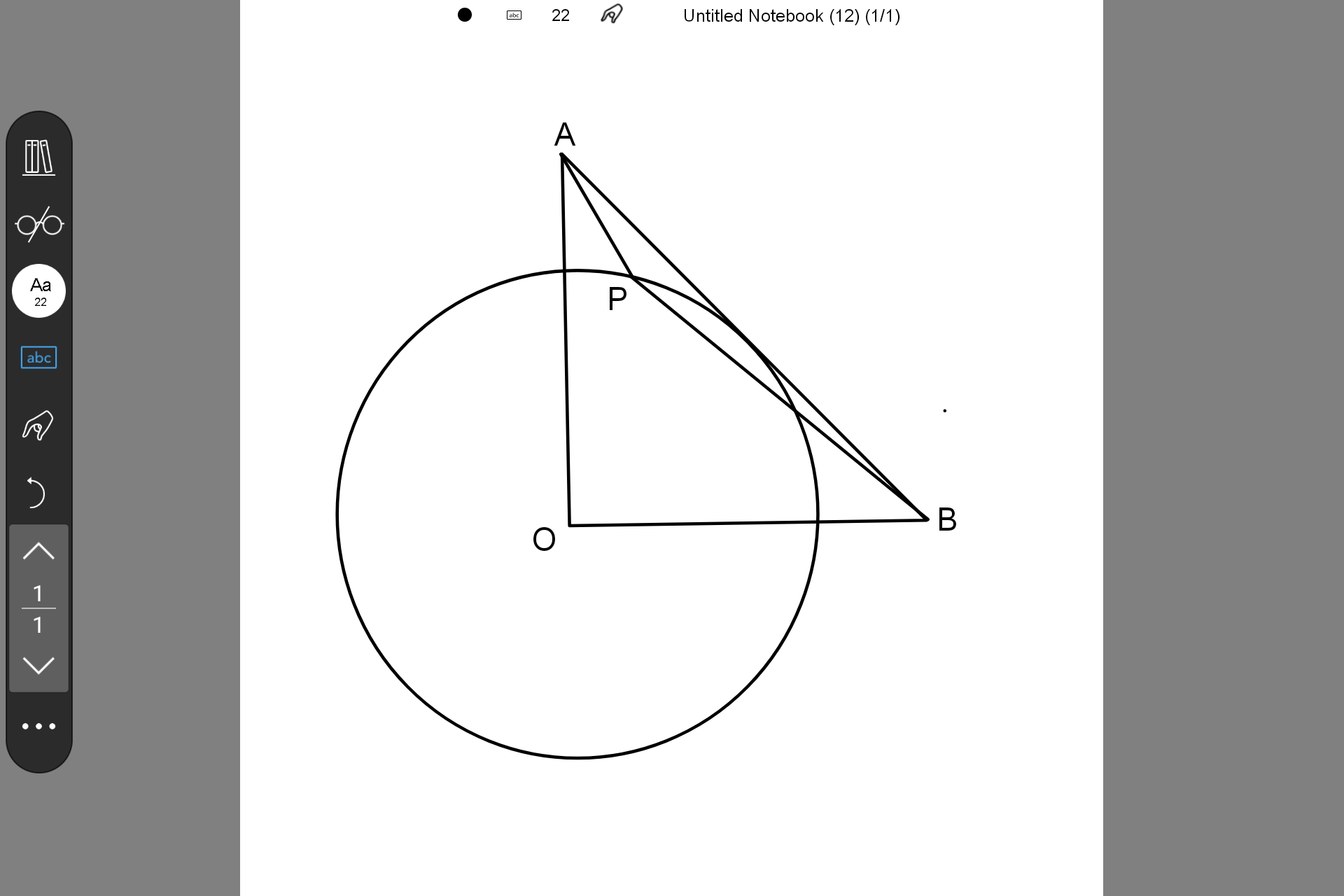
$\large{解法}$

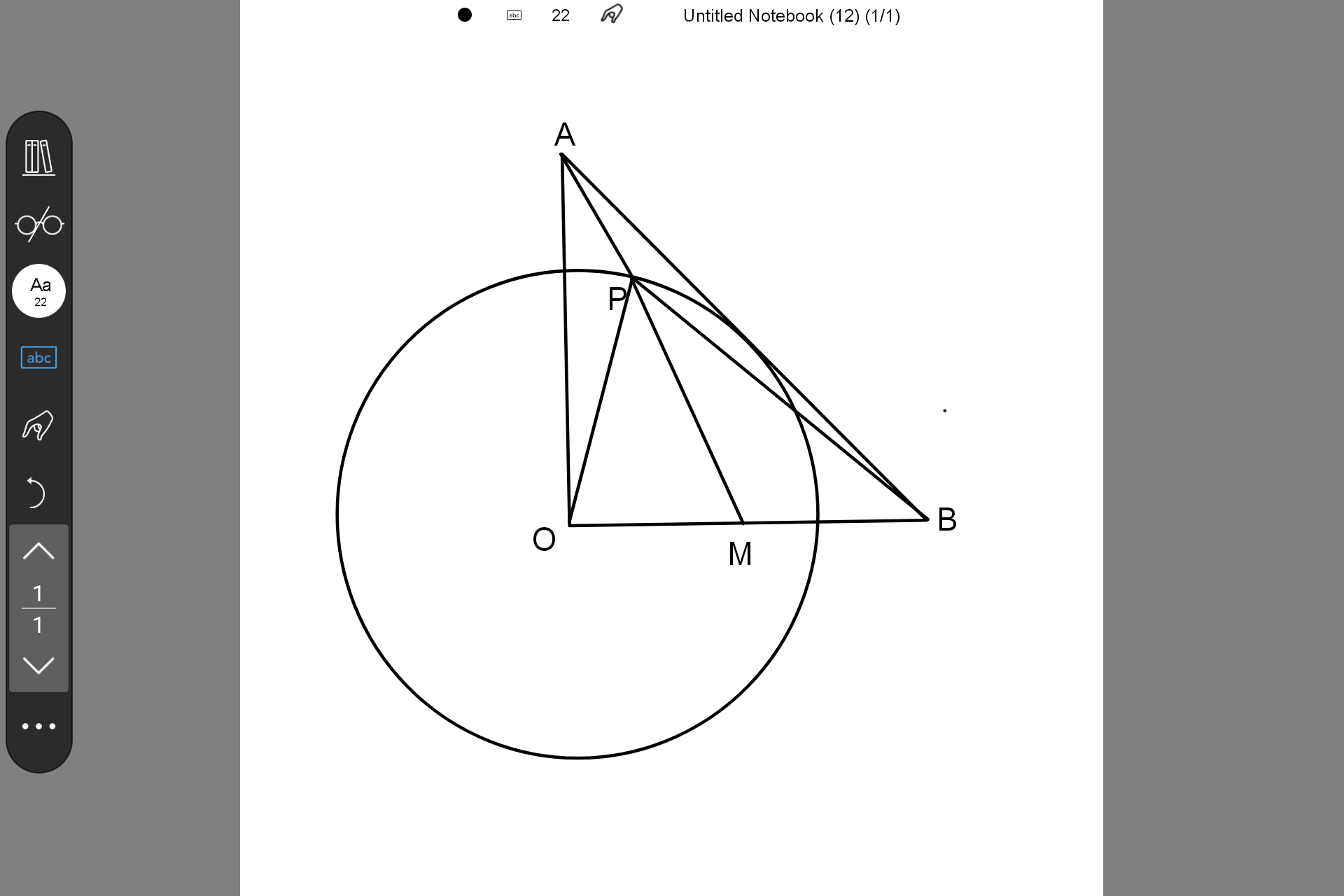
由切线＋等腰直角易得$OP=r=\sqrt{2}$

注意到$OB=\sqrt{2}OP$

取$OB$中点$M$，连接$PM$

$\because \frac{OB}{OP}=\frac{OP}{OM}=\sqrt{2} 且 \angle BOP=\angle POM$

$\therefore \triangle BOP \sim \triangle POM$

$\therefore BP=\sqrt{2}PM$

$\therefore BP＋\sqrt{2}AP=\sqrt{2}(PM＋AP)$

$易知当P，B，M三点共线时PM＋AP_{min}=AM=\sqrt{5}$

$\therefore \sqrt{2}AP＋BP_{min}=\sqrt{10}$

$\large{变式}$

如图，$\triangle ABO$中，$AO=4，BO=3$，$\angle O=90^\circ$，$r=2$，$P$为圆上任意一点，求$\frac{1}{2}AP＋BP$最小值