物理

Euler积分理论

一口气看完

前言：

前几天我的一个初一同学问了我这样一道题：

                        如何化简$\frac{n!}{n^n}$

这个问题是小学二年级的化简题，不难注意到，原式可以化为$\lim_{n \to \infty} \frac{n!}{n^n} = 0$

正文部分

那么如何严格证明上面这一坨的极限一定等于0，小学二年级老师教过我们，极限下趋于0，但永远无法取到0。那么如何面对同学的嘲讽呢？那你就受着呗()啊不，我们可以举几个例子瞧一瞧。

尝试分解一下，

$\frac{1}{n} \cdot \frac{2}{n} \cdot \frac{3}{n} \cdot \frac{4}{n} \cdots \frac{n}{n}= \frac{1 \cdot 2 \cdot 3 \cdots n}{n^n} = \frac{n!}{n^n}$

有这个式子，不难看出当n趋于∞时，整个式子的值就趋于0。如果我们还不放心，可以画一个大概图像出来：

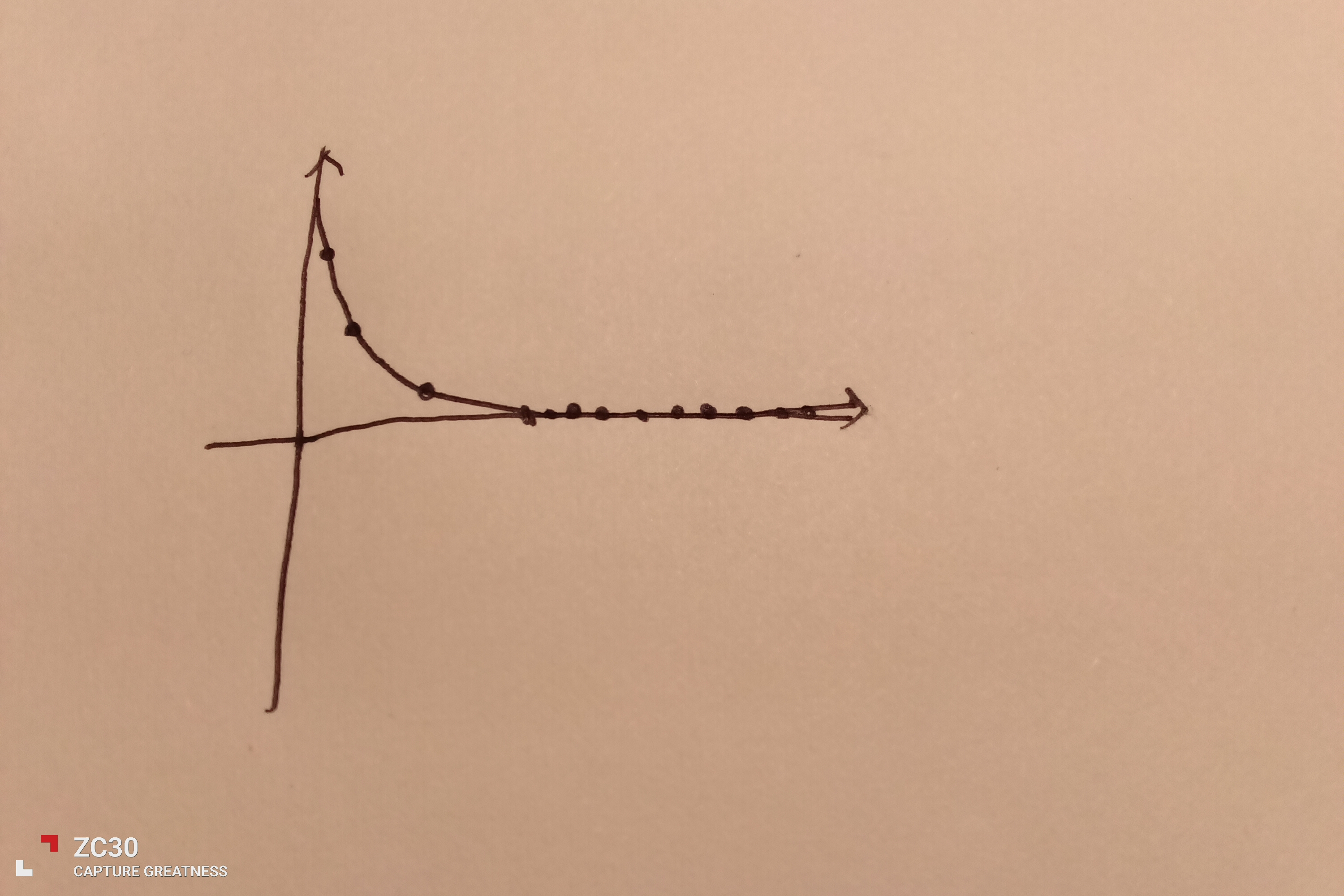
这个不是0我()好吧

所以我们把这个图像缩放得到一个通式如下，

令$q_{n+1} = \frac{(n+1)!}{(n+1)^{n+1}}$ ，那么$q_n = \frac{n!}{n^n}$，由这两个式子，不难得出：

$\frac{q_{n+1}}{q_n} = \frac{(n+1)!}{(n+1)^{n+1}} \cdot \frac{n^n}{n!}$

$= \frac{(n+1)!}{n!} \cdot \frac{n^n}{(n+1)^{n+1}}$

$= (n+1) \cdot \frac{n^n}{(n+1) \cdot (n+1)^n}$

$= \left( \frac{n}{n+1} \right)^n $

(托式计算格式可能不太整齐)，那么由于：

$e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n$

$= \lim_{n \to \infty} \left(\frac{n+1}{n}\right)^n$

所以，上面这个式子就等于$\frac{1}{e}$

那么恭喜你，被欧拉附体了()。为什么说被欧拉附体了呢？因为欧拉也遇到了这样一个问题为

                   证明  $\lim_{n \to \infty} \left( \frac{n!}{n^n} \right)^{\frac{1}{n}} = 0^0$

一般我们看到这个式子，都会想把n！从离散状态变换成有序的数列也就是$n! \to \Gamma(x)$，使其变成一个Gamma函数的形式。这样我们就可以使用洛必达法则求解了。那么为什么不行呢？有的同学就要问了，主播主播，Gamma函数不是有式子吗？

我们来看这个式子，$\Gamma(x) = \int_0^\infty t^{x-1} e^{-t} \, dt$

首先我们要明确一点，我们对于x导数，对于t积分，那么x导起来会非常麻烦。

那么到底该怎么做呢，欧拉提供了一种方法。

令$E = \lim_{n \to \infty} \left( \frac{n!}{n^n} \right)^{\frac{1}{n}}$

则$\ln E = \ln \lim_{n \to \infty} \left( \frac{n!}{n^n} \right)^{\frac{1}{n}}$，至于为什么要取对数呢，你猜()

$= \lim_{n \to \infty} \ln \left( \frac{n!}{n^n} \right)^{\frac{1}{n}}$

$= \lim_{n \to \infty} \frac{1}{n} \ln \left( \frac{n!}{n^n} \right)$

$= \lim_{n \to \infty} \left( \frac{1}{n} \ln\left(\frac{1}{n}\right) + \frac{1}{n} \ln\left(\frac{2}{n}\right) + \cdots + \frac{1}{n} \ln\left(\frac{n}{n}\right) \right)$

画一个图

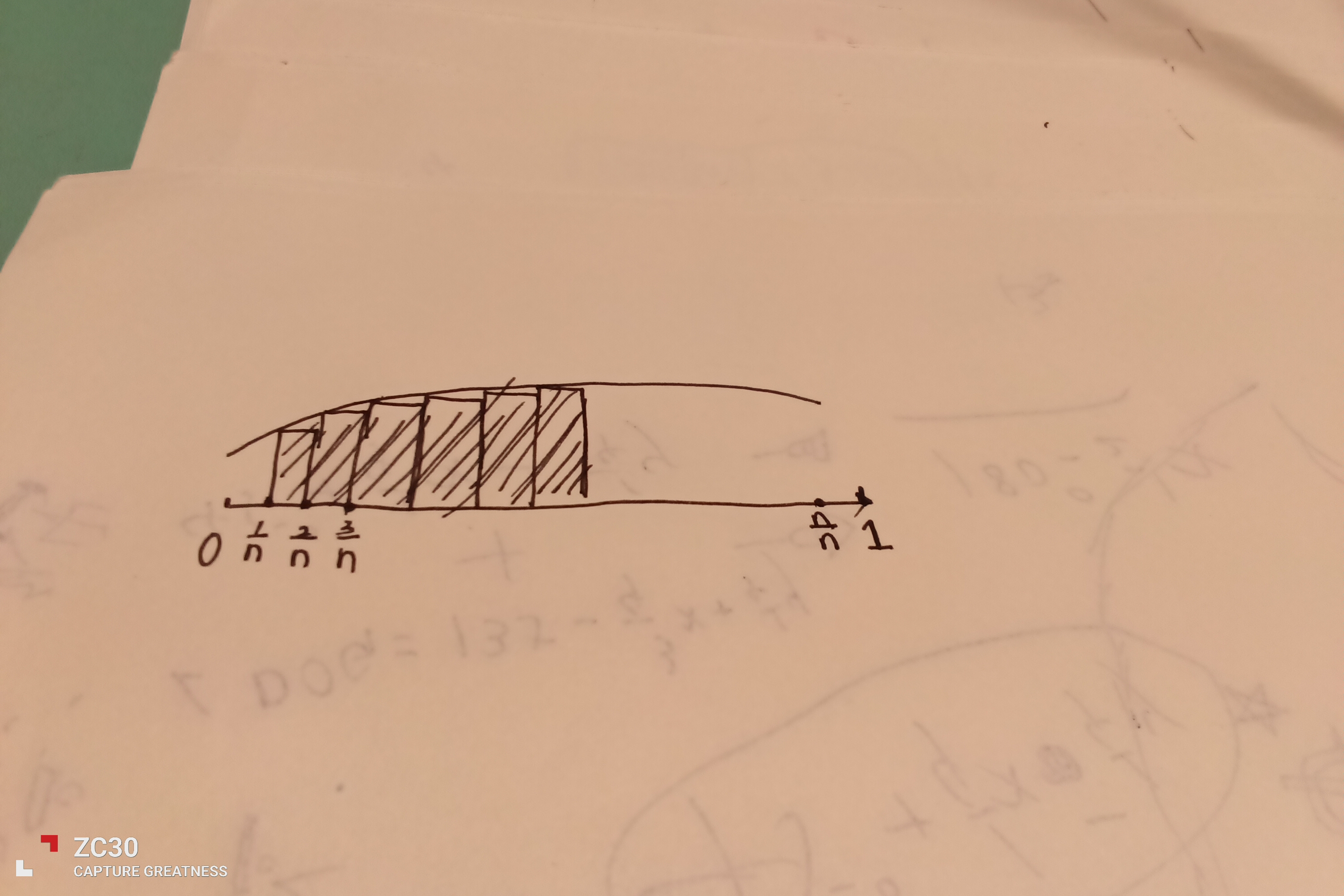
我们所要求的，就是阴影面积，上图没画全。

那不就是一个积分吗

所以原式等于$\int_0^1 \ln(x) \, dx $

那么接下来怎么办？评论区更完。