数学 那年那些几何⚪
有几何好题或其他芝士🧀可发评论区(贴主也会发)(这个贴主也是又更上了🙃)
此帖主要展示一些贴主发现或看到的几何模型及讲解,例题,难度中等,不定时更新,适合学了一段时间几何的竞赛僧(对其中题目有不同证法的或有错误的欢迎发表😀)(由于一些证明过程复杂,所以显然的部分会略加简写)
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
第一个构型是贴主偶然发现的,并拟写了一道题。
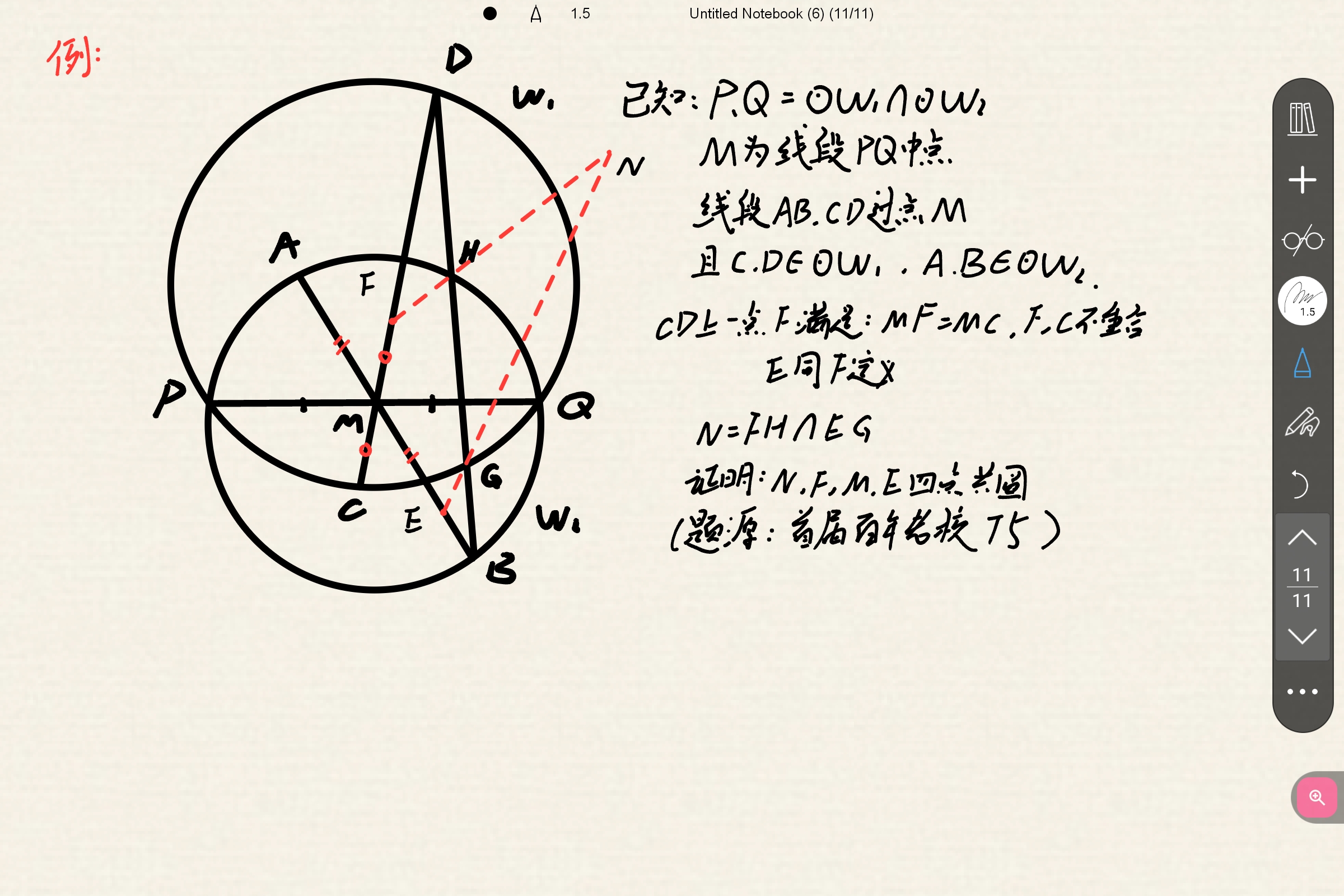
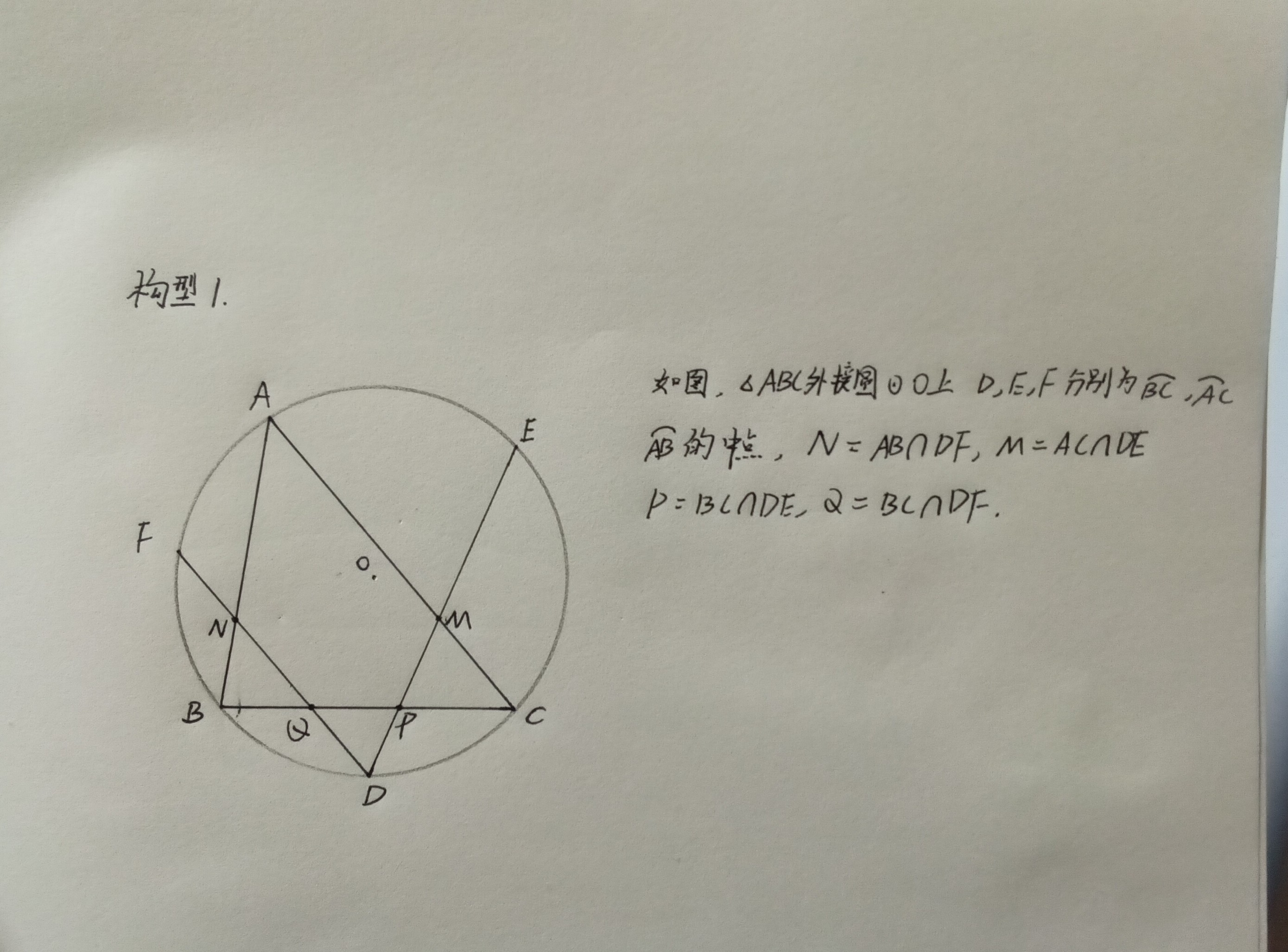 在此构型中,我们不难发现P、Q、F、E四点共圆(自证),而且我们发现连接MN, 似乎MN∥AB,借此我们再猜测M、 N、 F 、E四点共圆,如果共圆成立,那么平行也就显然了,我们给出如下证明:
在此构型中,我们不难发现P、Q、F、E四点共圆(自证),而且我们发现连接MN, 似乎MN∥AB,借此我们再猜测M、 N、 F 、E四点共圆,如果共圆成立,那么平行也就显然了,我们给出如下证明:
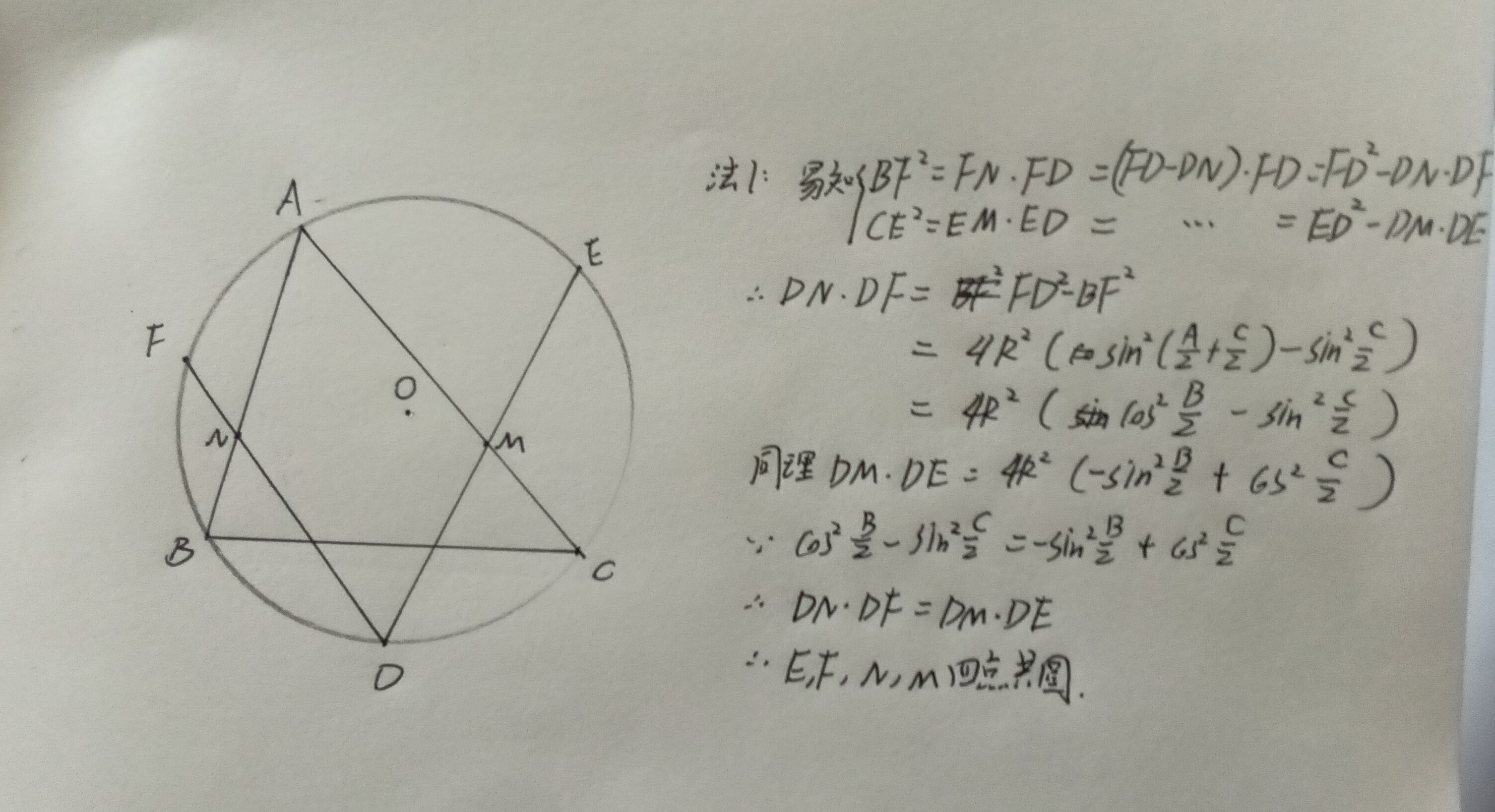
(贴主也有纯几证法但上述证法相对简单,便不多加赘述,只需做出内心I,证明I为ΔDEF垂心,再倒角即可)
由此出出一道题,知道上述构型后此题难度不高,但若不知道,则较难解决,题目如下:
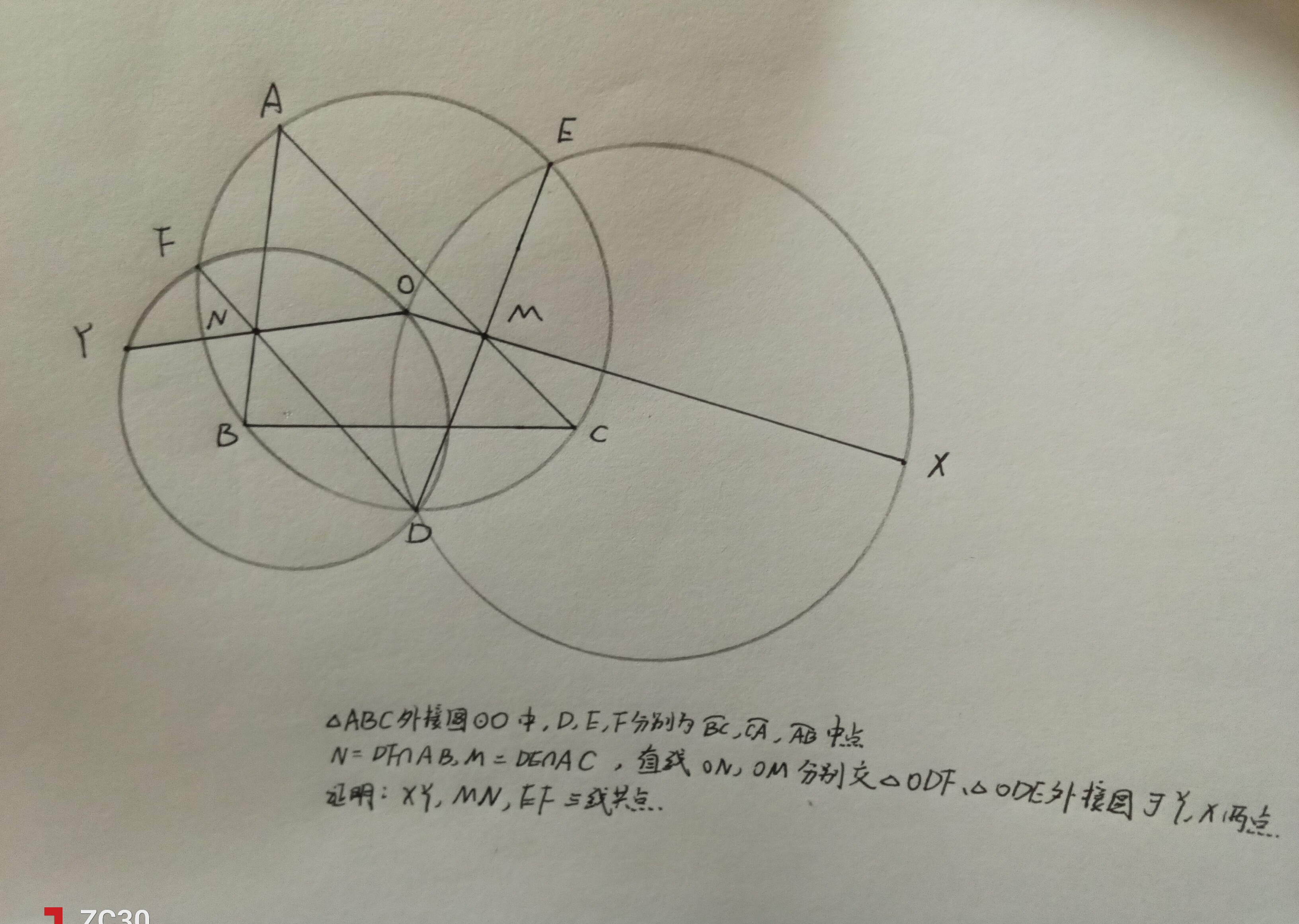
证明:
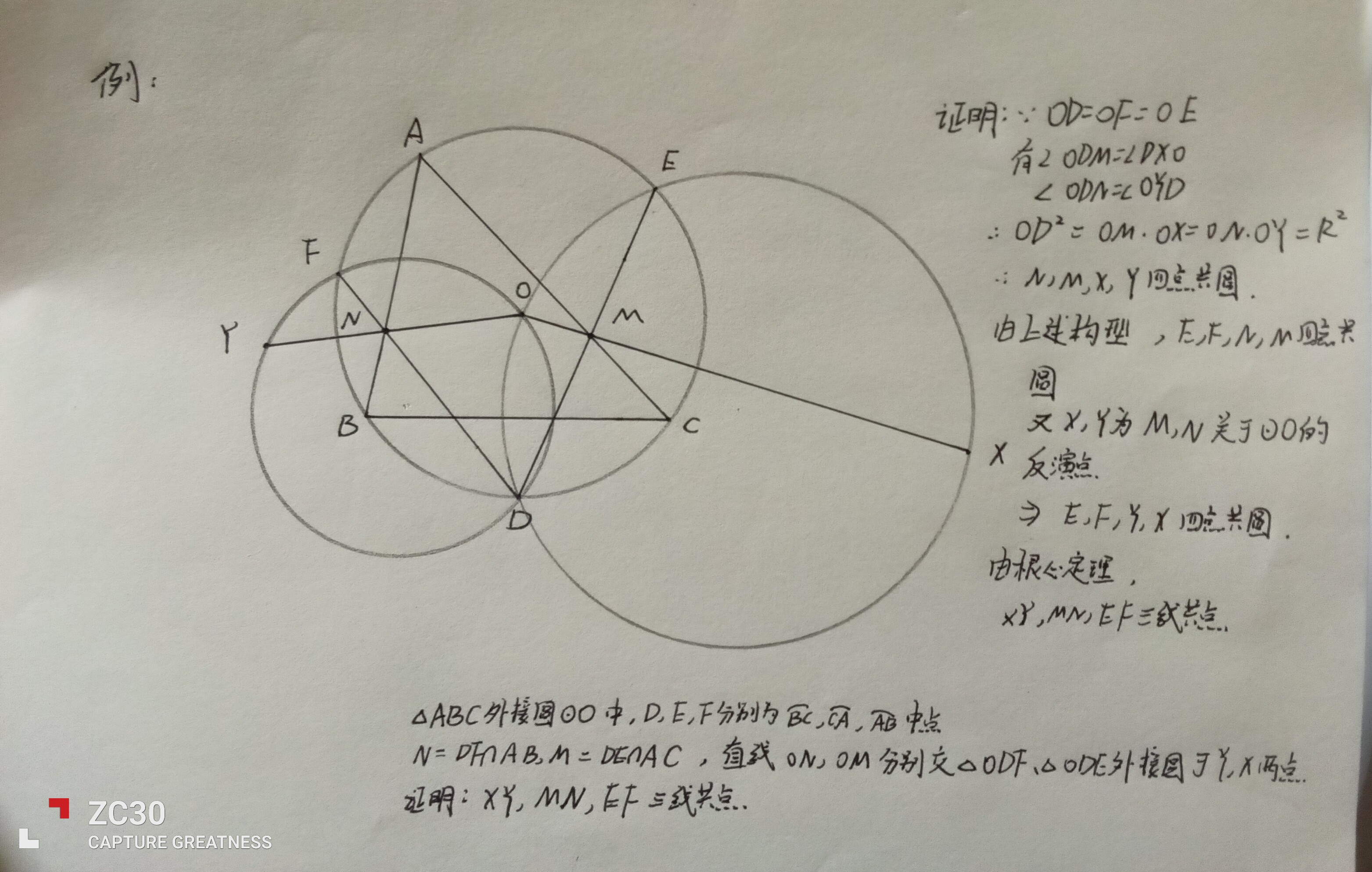 (若未学过反演,也可用相似证明第三个共圆,贴主同学证的)
(若未学过反演,也可用相似证明第三个共圆,贴主同学证的)
(感觉第一个构型和例题是不是简单了一些😥😥😥)
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
这是伊朗2016中级几何第5题(而贴主也多次看到这个结构),做完后我想便研究此图有什么神奇的性质

此题解法(更多解法详见数之谜♿♿♿)

于是like this
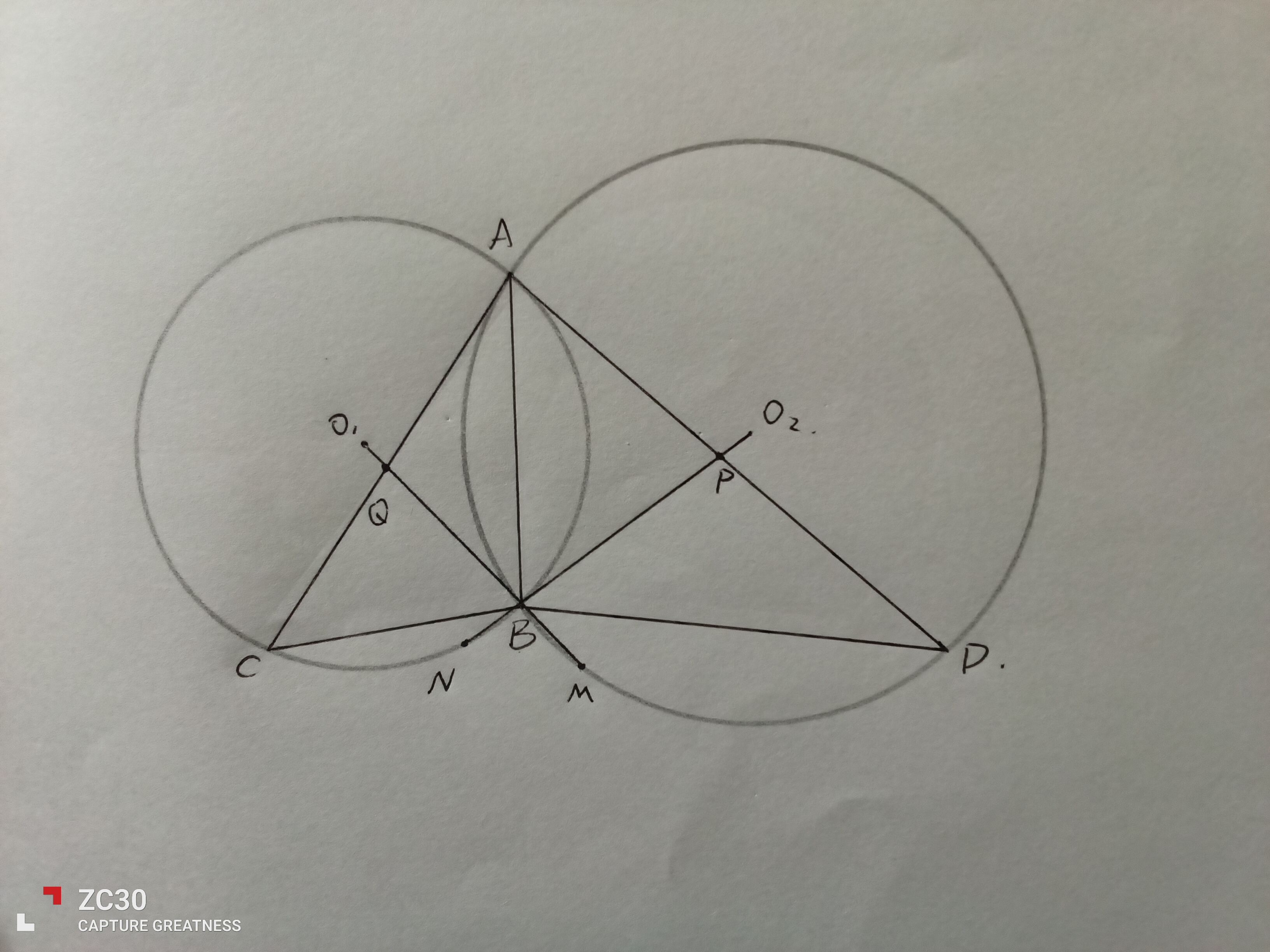
有P,Q,M,N共圆(ΔABD∼ΔCBA; P,Q;O₁,O₂为位似对应点 ; 且P,Q,O₁,O₂四点共圆. 即证)
(关于这个构型的性质贴主目前没太多想法☹️)
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
下一个吧😶😶😶也是双圆(这个是在万喜人绿本里的)
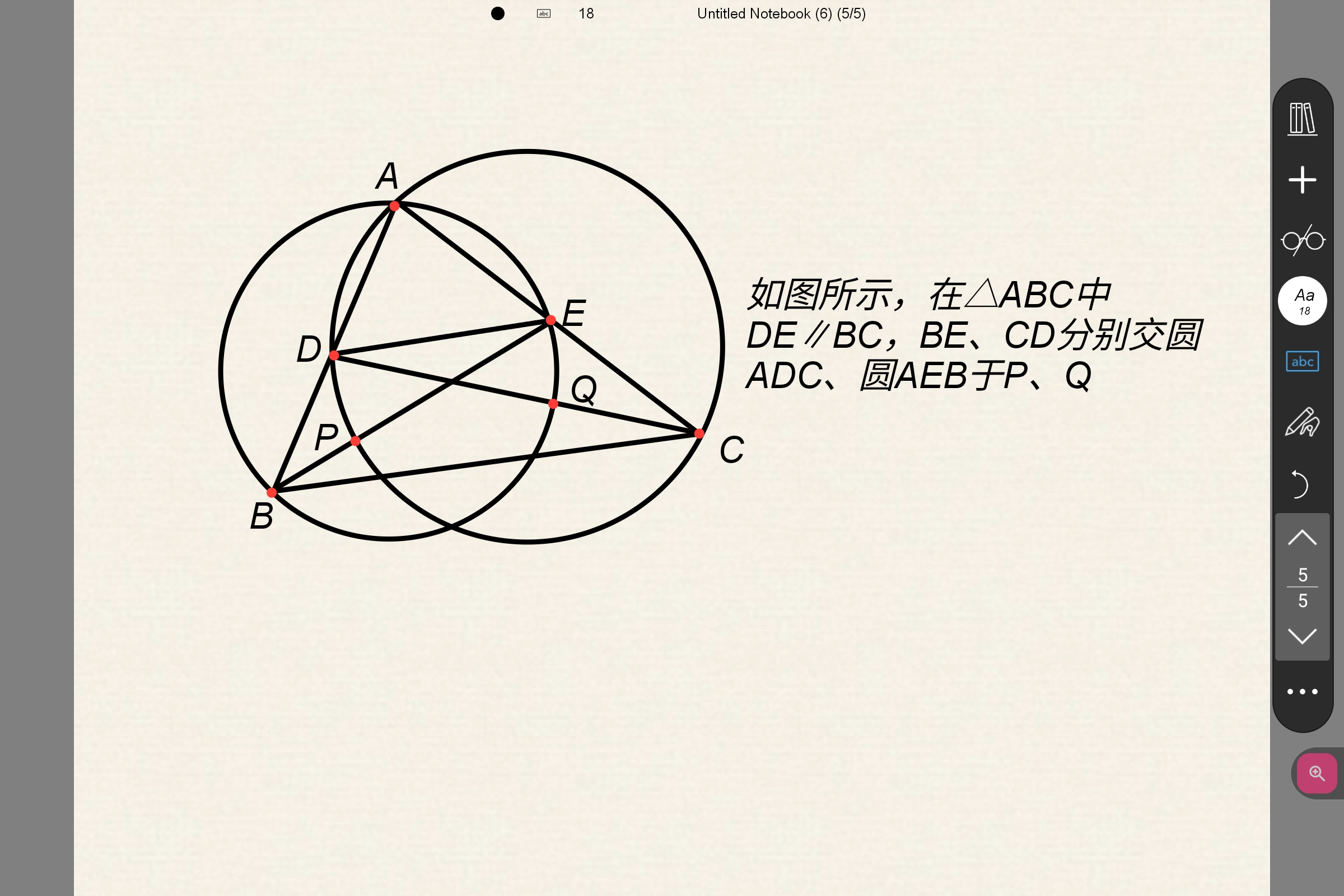
在上图中我们发现很多性质:
(ⅰ) B、C、P、K四点共圆
(ⅱ) D、E、K、P四点共圆
(ⅲ)∠BAP=∠CAK(原题要证)
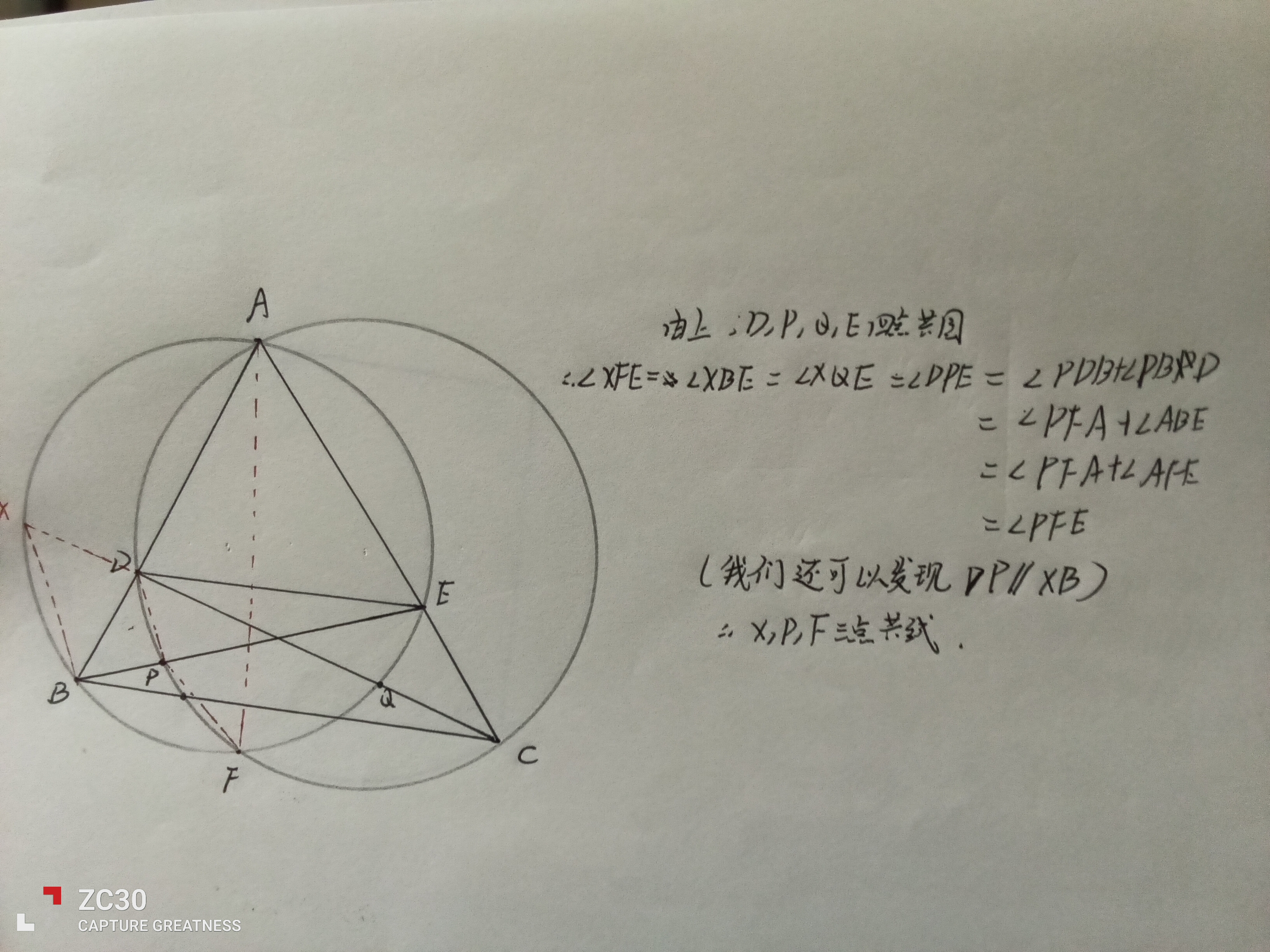
不想码字直接发答案吧🤤🤤🤤

然后我们设两圆另一交点为F
发现BP、DC; BK、BE分别与两圆交于同一点
倒角即可:
———————————————————————————————————————————————————————————————————
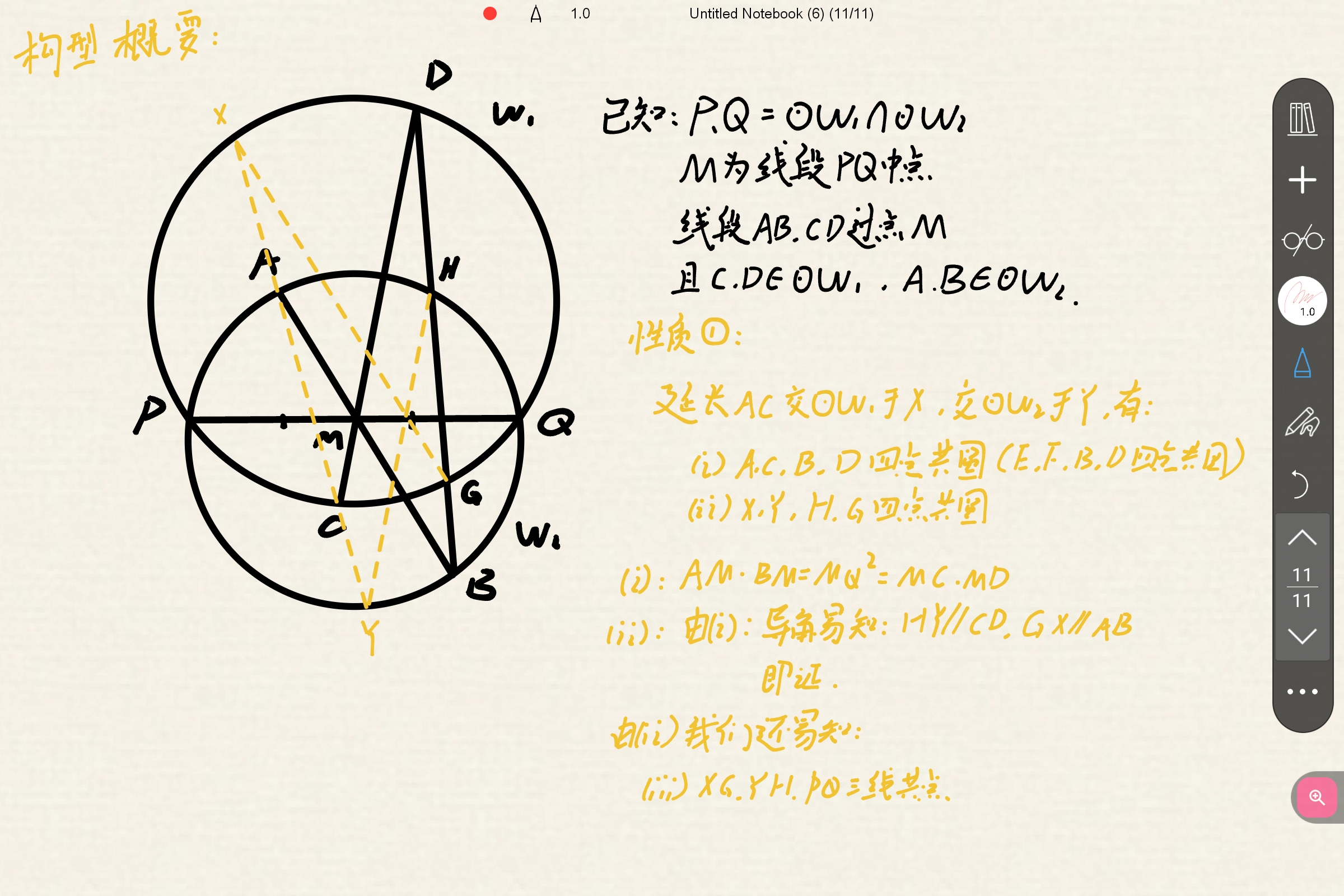
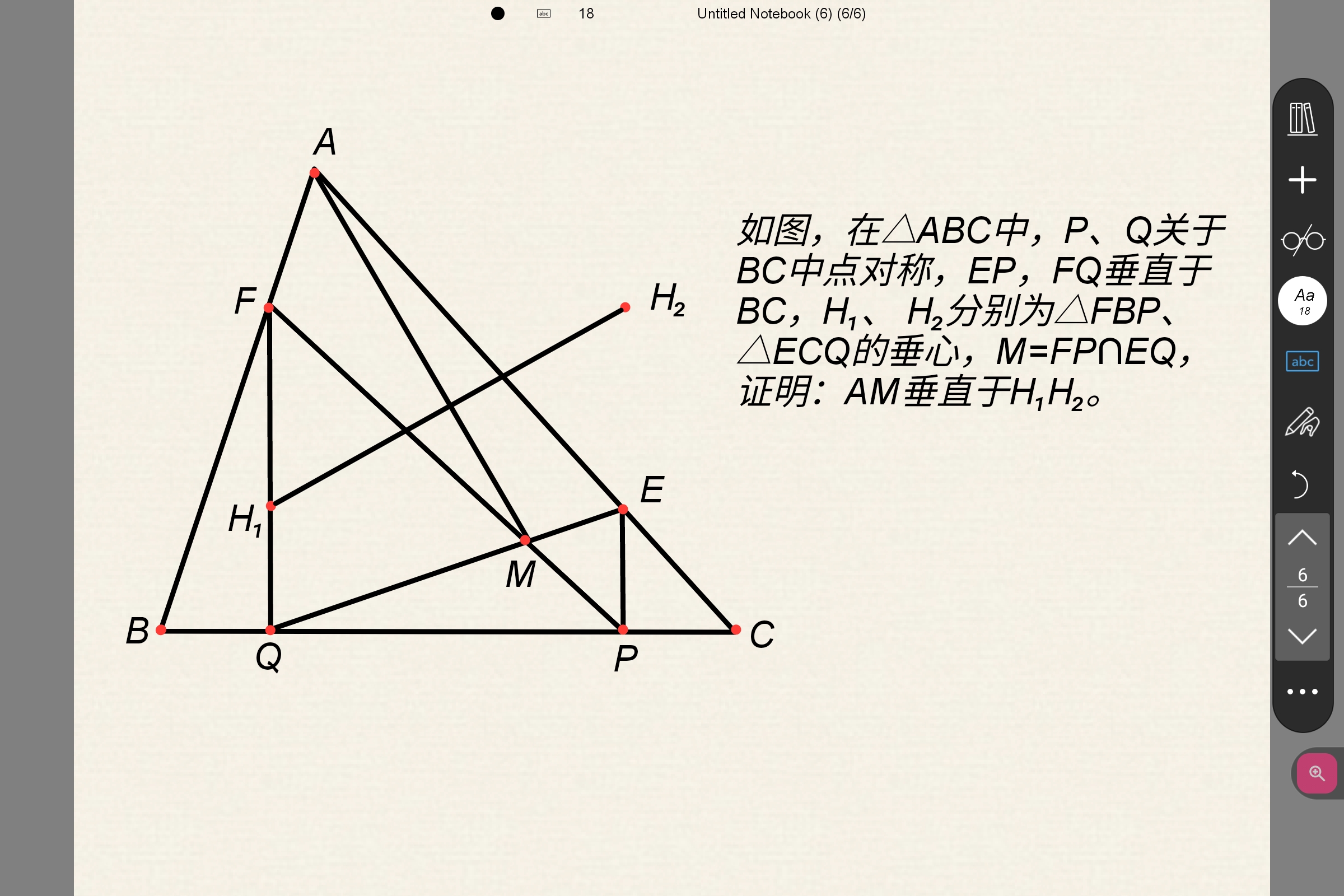
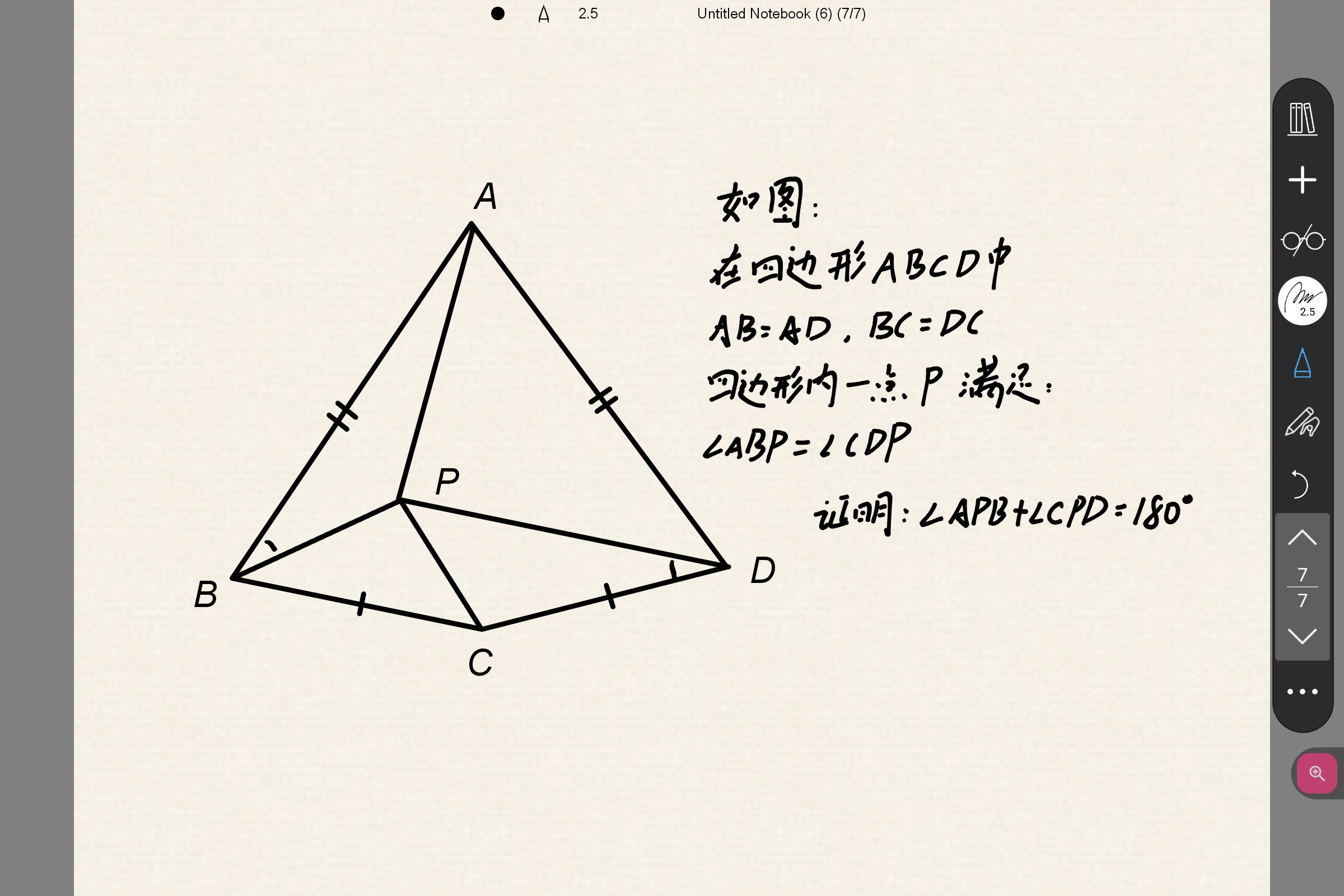
这里放个贴主做法,也可以反演做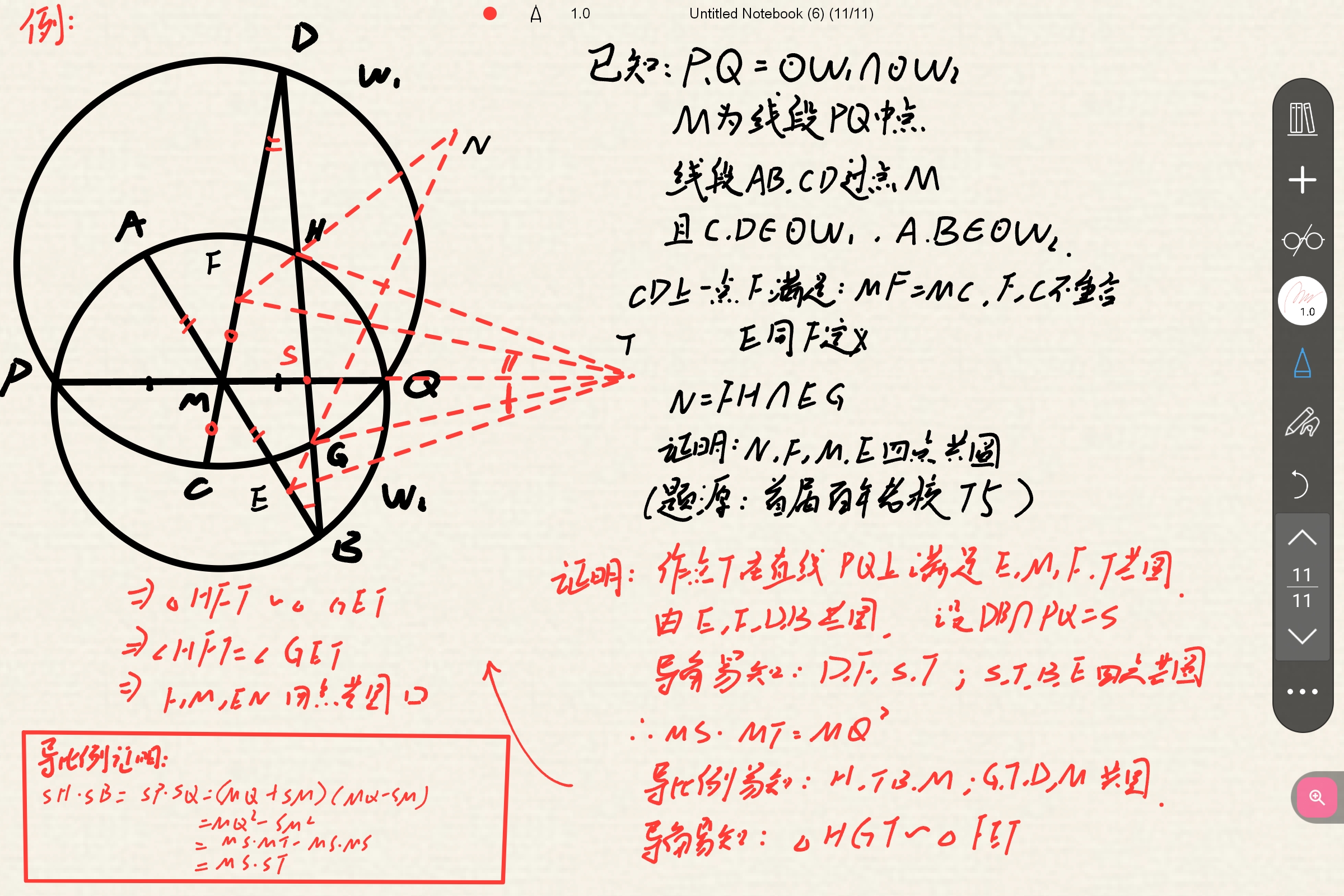

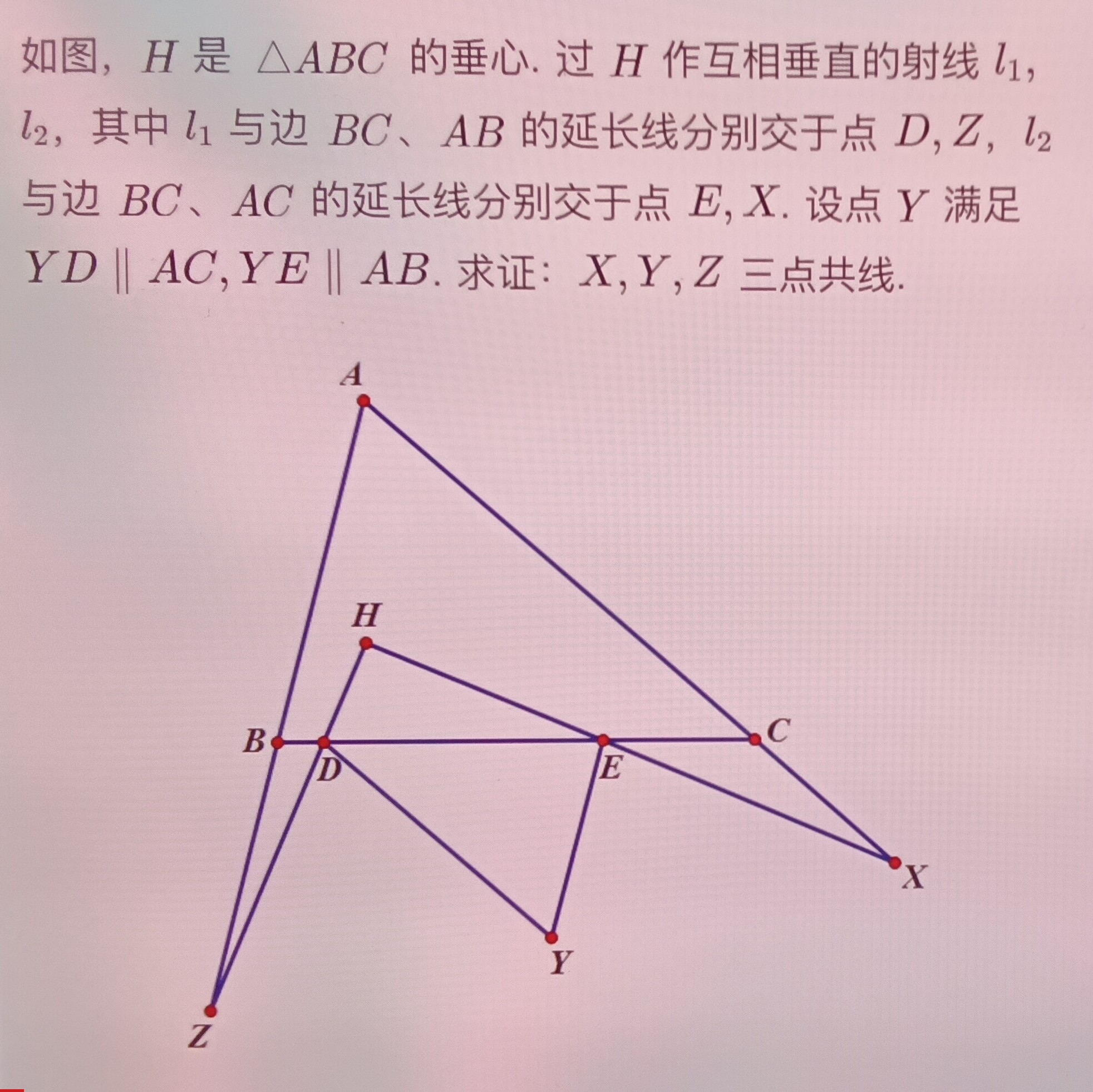
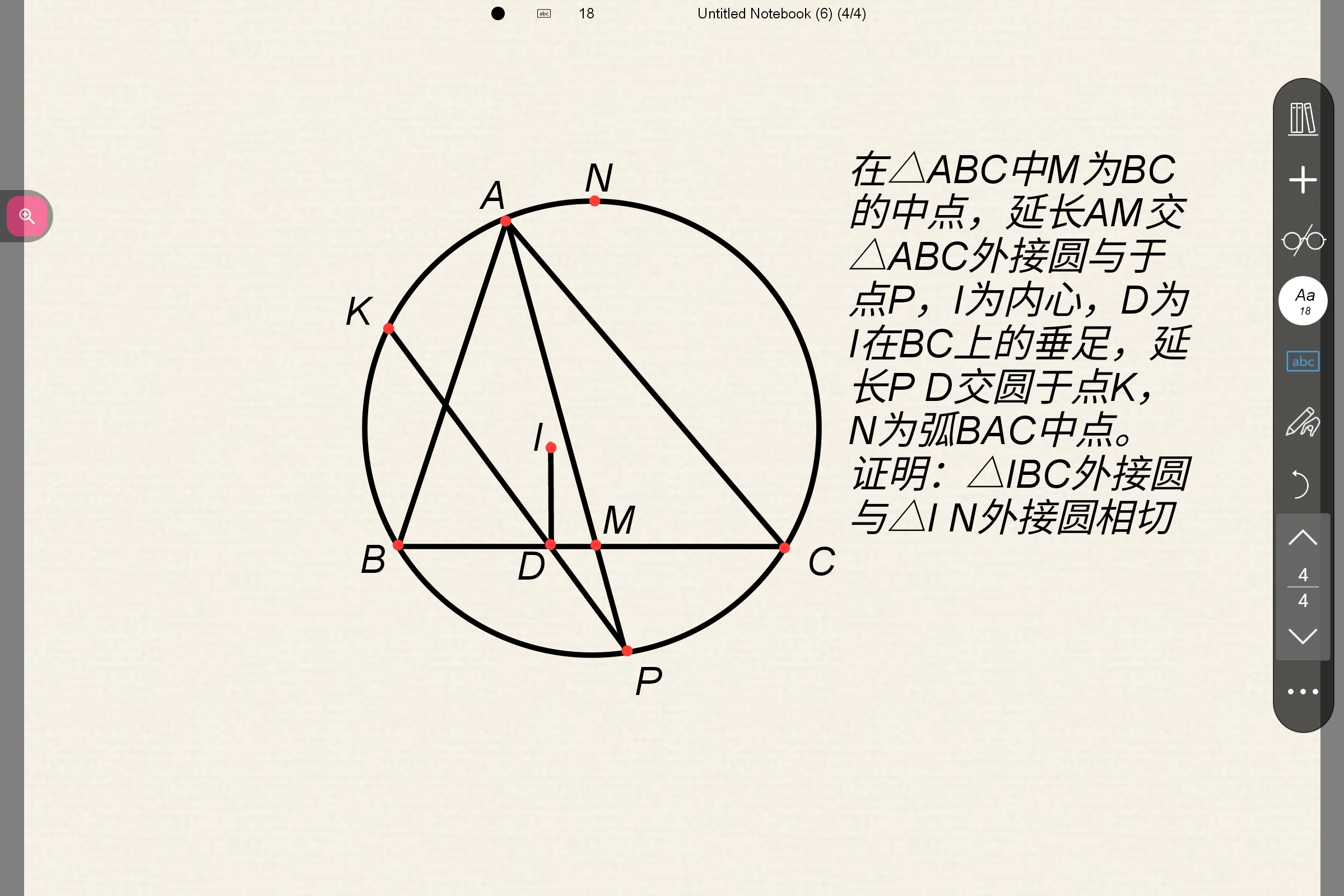



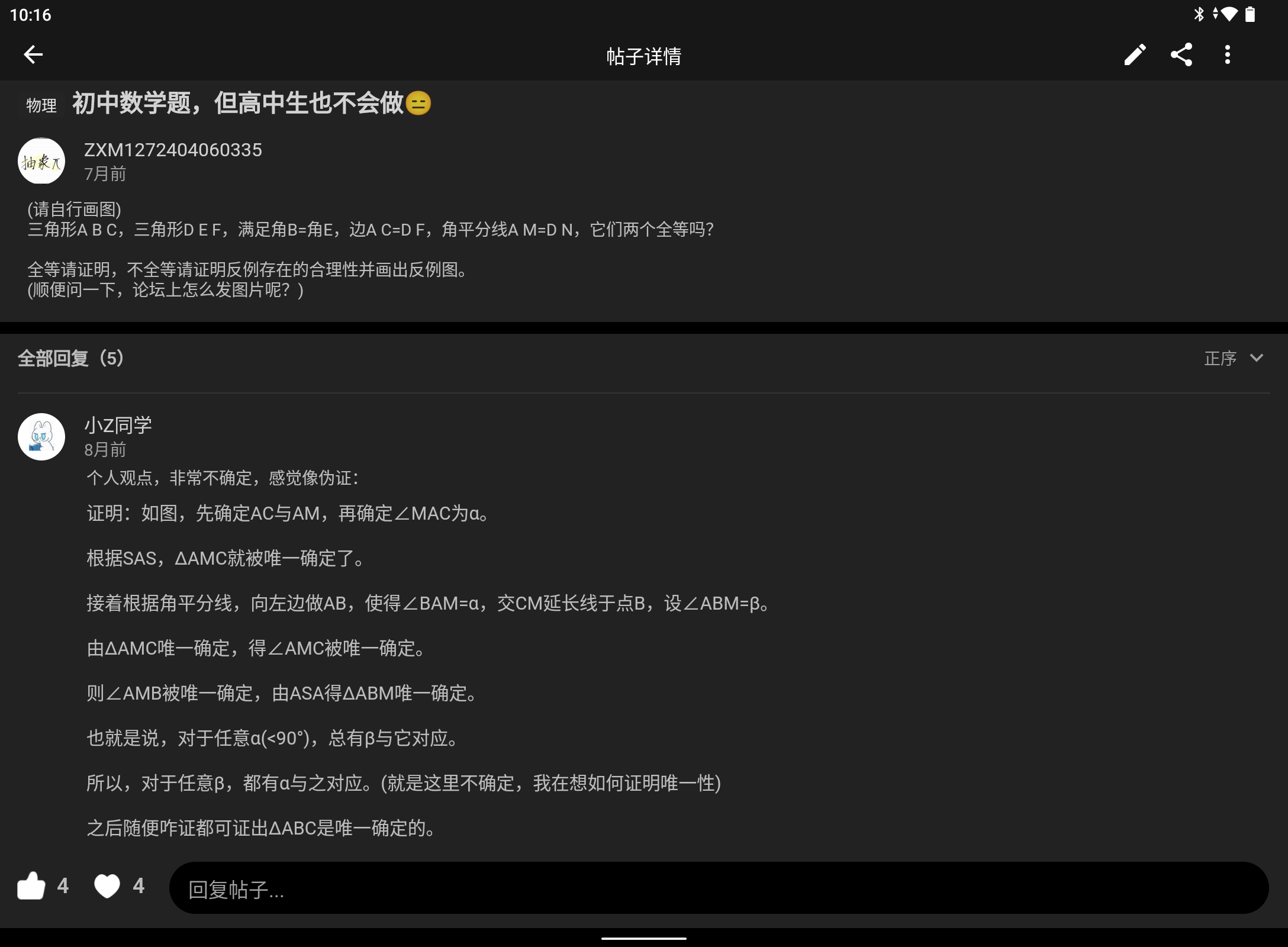 好像有反例,但我画不出来。
好像有反例,但我画不出来。