数学 数论、概率论在信息学中的应用
本帖中的^符号是幂符号,如2^3 = 2的3次方 = 2*2*2 = 8。
其中,1≤N,Q≤300000。
如果对一每一次询问(操作2)都将两个区间做差那么运算次数最坏为:N*Q次,即每次都是操作2,且区间长度趋近于N。
所以(N*Q)max=300000*300000=9* 10^10。
温馨提示:本题时限为1s,主流编程语言没秒的运算速度为10^8,所以该方法会超时。
考虑使用哈希算法和线段树数据结构解决本题。
先讲哈希算法
哈希算法多用于字符串到整数的映射。想想将一个字符串:ILoveMath怎么变成一个整数?这也许让人匪夷所思不过其实不难。在信息学中每个字符都有编号,就是每个字符都是个数字,于是我们的哈希算法就这样将字符串变成了整数:
Hash(S)≡p^S[1]+…+p^S[n] (mod M)
其中p为质数,M为极大质数。Hash叫哈希函数
由于M为极大质数(差不多10^9)所以让两个不同字符串的概率为1/p(就是一个字符相等机即p^S[i]相等的概率) ^ n (n个字符)即:1÷(n^p),几乎为零,当然p也不是越大越好,最好不要超过√M。总之不要太大,一般M取1999999997时p可能也才97,100以内的质数完全满足了p的需求!
回归正题,哈希和这题有什么关系呢?已经说过,字符实质是整数可运算,而本题的数列本来就是数那么用哈希不就很正常了吗?
而N那么大足足300000,重复概率仅为1÷(300000^p)这个p就是之取5,重复的概率就可以忽略不计了吧?
其次是线段树
这是一种树形数据结构,可以在N此的复杂度建树并在log N的复杂度查询(复杂度可理解为运算次数)。
比较复杂这里看图
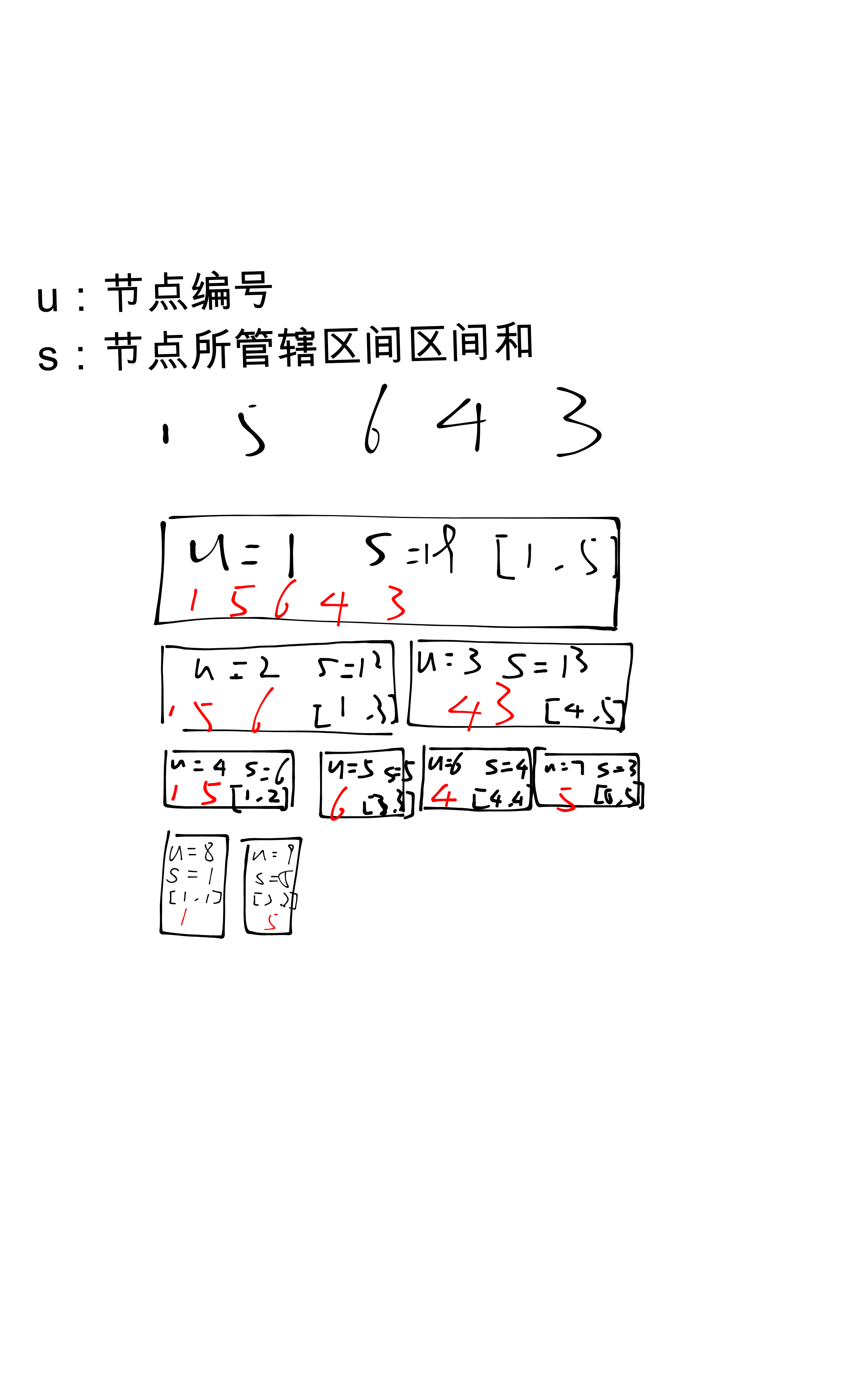
将数列分为几个子序列实现上述功能,具体实现不展开讲述。当然s可以是我们想维护的任意可维护值。
本题解法
讲课这么久,被踢本题做法将求连区间所有数减其最小值后的哈希。
即:在原数列用哈希算法算出的值除以p^(min),由于有模数所以是乘p^(min)的逆元。
怎么求?这是M为极大质数的优势就体现出来了,由费小:
p^(M-1)≡p mod M
p^(M-2)≡1 mod M
所以p^(M-2)就是逆元。
最后判断求出的两个值是否相等即可!
下期分享本题的用三角函数判断两区间是否满足条件的解法!
