数学

海伦公式及秦九韶公式的推理

(LaTeX后期补)斗胆放O区来了

如果给你一个三角形的三边长，让你求三角形的面积，你咋办？是${\frac{1}{2}{×ab×sin C}}{？是}{\frac{1}{2}{×a×h_a}}$？是……好像都不太行。这时，我们注意到(拉马努金附体)，三角形的高可以用勾股定理来算！！！(拉马努金立大功)

有了思路，那必须干它！！！🤓🤓🤓第一步，先作高！

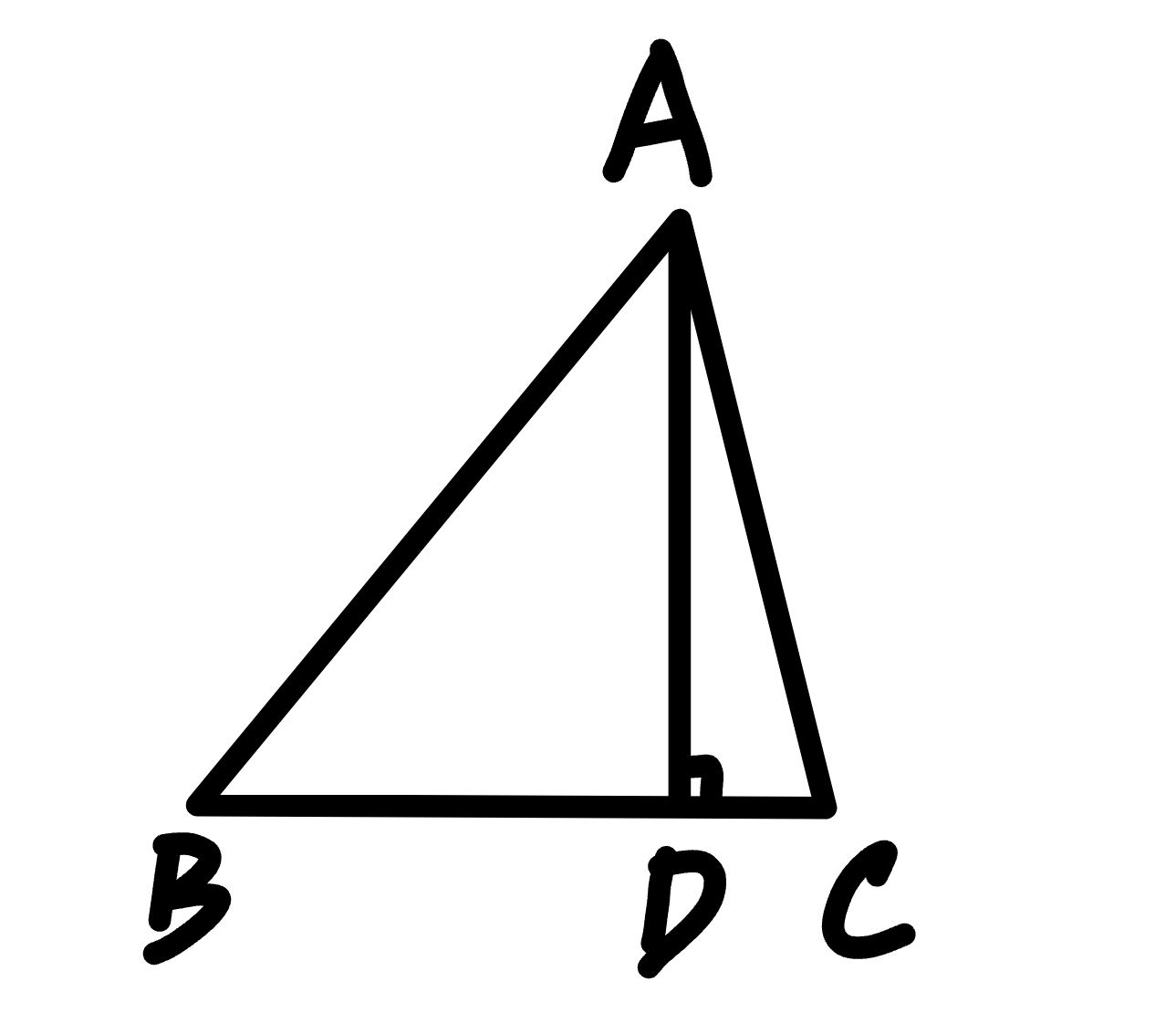
过点$A$作$AD$垂直于$BC$于$D$

咱先设$BD=x$，则$CD=a-x$

那勾股定理这不来了吗

${{x^2}{+}{AD^2}{=}{c^2}}$，解得${{AD^2}{=}{c^2}{-}{x^2}}$

另一边，${{(a-x)^2}{+}{AD^2}{=}{b^2}}$

得${{AD^2}{=}{b^2}{-}{a^2}{+}{2ax}{-}{x^2}}$

又${{∵}{AD^2}{=}{AD^2}}$(这不用我说吧)

${∴}{c^2}{-}{x^2}{=}{b^2}{-}{a^2}{+}{2ax}{-}{x^2}$

解得${x=}\frac{{a^2}{-}{b^2}{+}{c^2}}{2a}$

然后再把$x$代入(挑个最简单的代入)

${{∴}{AD^2}{=}{c^2}{-}{x^2}}$

${{=}{c^2}{-(}{\frac{{a^2}{-}{b^2}{+}{c^2}}{2a}}{)^2}}$

${{=}\frac{{4}{a^2}{c^2}}{{4}{a^2}}{-}\frac{{(}{a^2}{-}{b^2}{+}{c^2}{)^2}}{{4}{a^2}}}$

${{=}\frac{{4}{a^2}{c^2}{-}{(}{a^2}{-}{b^2}{+}{c^2}{)^2}}{{4}{a^2}}}$

${{∴AD=}\sqrt{\frac{{4}{a^2}{c^2}{-}{(}{a^2}{-}{b^2}{+}{c^2}{)^2}}{{4}{a^2}}}}$

${{=}\frac{\sqrt{{4}{a^2}{c^2}{-}{(}{a^2}{-}{b^2}{+}{c^2}{)^2}}}{2a}}$

我们可以发现，根号下的部分是一个平方减平方的形式，所以我们可以用平方差公式暴力展开

${{∴AD=}\frac{\sqrt{{(}{2ac+}{a^2}{-}{b^2}{+}{c^2}{)}{(}{2ac}{-}{a^2}{+}{b^2}{-}{c^2}{)}}}{2a}}$

${{=}\frac{\sqrt{{[(}{a^2}{+}{2ac}{+}{c^2}{)}{-}{b^2}{)]}{[-(}{a^2}{-}{2ac}{+}{c^2}{)}{-}{b^2}{)]}}}{2a}}$

${{=}\frac{\sqrt{{[(a+c}{)^2}{-}{b^2}{]}{[-(a+c}{)^2}{+}{b^2}{]}}}{2a}}$

${{=}\frac{\sqrt{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}}{2a}}$

然后到收官阶段

${{S_{{\Delta}{ABC}}}{=}\frac{1}{2}{BC·AD}}$

${{=}\frac{1}{2}{a·}\frac{\sqrt{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}}{2a}}$

${{=}\frac{1}{4}\sqrt{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}}$

这时将p引入：令${{p=}\frac{a+b+c}{2}}$

于是${{a+c+b=2p}}$

${{a+c-b=2(p-b)}}$

${{b+a-c=2(p-c)}}$

${{b-a+c=2(p-a)}}$

所以原式${{=}\frac{1}{4}\sqrt{2p·2(p-b)·2(p-c)·2(p-a)}}$

${{=}\frac{1}{4}\sqrt{16·p(p-a)(p-b)(p-c)}}$

${{=}\frac{1}{4}{×4}\sqrt{p(p-a)(p-b)(p-c)}}$

${{=}\sqrt{p(p-a)(p-b)(p-c)}}$

这就是大名鼎鼎的海伦公式：${{S_{{\Delta}}}{=}\sqrt{p(p-a)(p-b)(p-c)}{(p=}\frac{a+b+c}{2}{)}}$