物理

讲点你不知道的尺规作图(冷？)知识——从作正十七边形谈起

$事先声明：未完结前，请勿开楼。$

$或许各位小时候都听过高斯曾一晚上就解决了一个世界难题，$

$而这个难题连牛顿都没解出来，那就是：$

$\large{仅用一把无刻度的直尺和一把圆规，作出一个正十七边形。}$

$这个故事广为流传，不过它是假的，真正作出正十七边形的另有其人。$

$但是高斯确实为解决这个问题做出了很大贡献，$

$因为他证明了正十七边形确实可以通过尺规来作出。$

$进一步地，他证明了：$

$\large{所有边数可以表示为2^{2^n}+1(n∈\mathbb{N})的正多边形都可以用尺规作出}$

$可以看出，n=2时，上式值为17，正十七边形是符合要求的多边形。$

$下面大致介绍一下作图思路：$

$我们要作正十七边形，重点是作出一个角，其弧度为\frac{2\pi}{17}，$

$更进一步地说，我们要知道这个角的一个三角函数值。$

$而我们的高斯同学就\sout{注意到}求出了以下式子：$

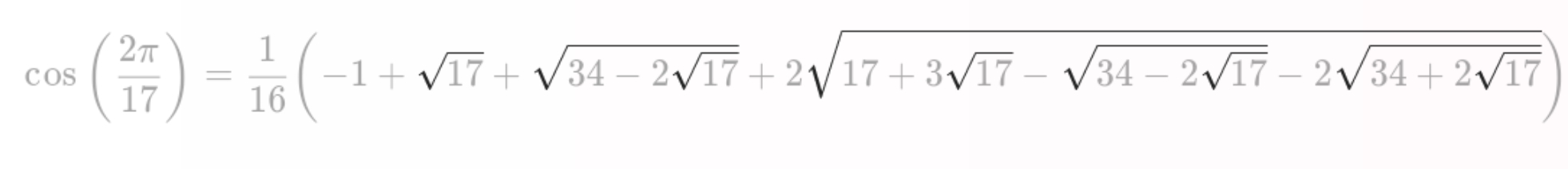
$可以看出，cos\frac{2\pi}{17}可以表示为一个只含加、减、乘、除和开平方五则运算的式子，$

$而这是尺规作图作出一个数的充要条件。这是为什么呢？这就是我们今天要来探讨的问题。$

$这个问题，将尺规作图这样一个几何问题，转化成了一个代数问题，$

$也或许能为我们今后解决其他的尺规作图问题提供一个新思路。$

$当然，这里许多证明可能不太严谨，请各位大佬见谅。$

$以上为引入部分$