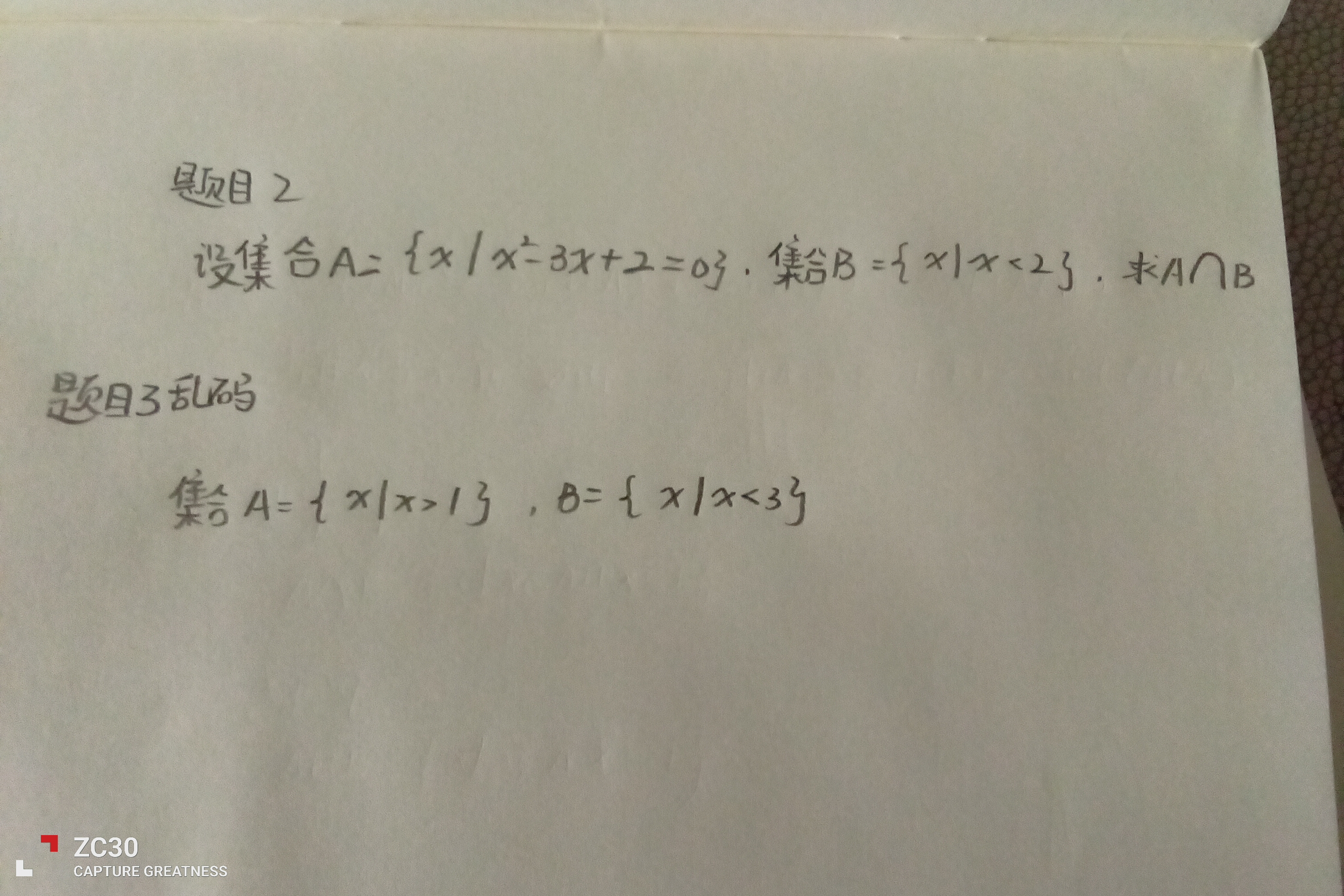- 时间正序
- 时间倒序
- 评论最多
- 1
一.集合与逻辑
1.集合
(1)定义:一些元素组成的整体叫做集合。
(2)集合内部元素与集合的关系: 1.属于:$\in$ 2.不属于:$\notin$
常见集合用语:1.自然数集:$N$ 2.正整数集:$N+$ 3.整数集:$Z$ 4.有理数:$Q$ 5.实数集:$R$
注意:构成集合的元素必须是确定的。
集合内元素的三大特性:确定性,互异性,无序性
确定性:集合中的每个元素都是确定的,要么$\in A$,要么$\notin A$。
互异性:集合中的元素没有相同的,同一个元素只能出现一次。
无序性:集合中的元素没有先后顺序。
(3)描述法与列举法
引例:表示出不大于16的非负偶数
列举法表示:{0,2,4,6,8,10,12,14,16};
表示出$x^2+ax+b$的解集
描述法:{x | $x^2+ax+b$}
2025.11.29日一更
一.集合与逻辑
4.子集与真子集,子集记作A⊆B或B⊇A,如果A⊆B,且A≠B,则称A是B的真子集
如果A⊆B且B⊆A,则A=B
结论:若集合A中有n个元素,那么集合A有$2^n$个子集,有$2^{n-1}$个真子集
空集∅:空集是不含任何元素的集合;空集是任何集合的子集;空集是任何非空子集的真子集。
5.交集与并集
交集:由属于集合A且属于集合B的所有元素所组成的集合,叫做A与B的交集,记作A∩B
即为A∩B={x | x∈A且x∈B}
并集:有属于集合A或属于集合B的所有元素所组成的集合,叫做A与B的并集,记作A∪B
即为A∪B={x | x∈A或x∈B}
交并集内部的运算法则
A∪A=A;A∩A=A;A∪∅=A;A∩∅=∅;
若A∪B=B,则A⊆B;若A∩B=B,则B⊆A。
真子集的写法(打不出来)

2025.11.30日第二更
预计今晚第三更,预告:下期将会有全集,补集,容斥原理
一.集合与逻辑
6.全集与补集
全集:如果一个集合包含所研究问题中涉及的所有元素,那么就称这个集合为全集,通常记作 $U$;
补集:对于一个集合 $A$,由全集 $U$ 中不属于集合 $A$ 的所有元素组成的集合称为集合 $A$ 相对于全集 $U$ 的补集,简称为集合 $A$ 的补集,记作 $C_U A$。
符号表示为:若 $A \subseteq U$,$B \subseteq U$,$C \subseteq U$,…,则 $U$ 为全集,
$ C_U A = \{x \mid x \in U, \text{且 } x \notin A\} $
$A \cap (C_U A) = \varnothing \quad C_U U = \varnothing \quad C_U \varnothing = U$
$A \cup (C_U A) = U \quad C_U (C_U A) = A$
$C_U (A \cap B) = (C_U A) \cup (C_U B), \quad C_U (A \cup B) = (C_U A) \cap (C_U B)$
数集:$\{x \mid p(x)\}$
点集:$\{(x, y) \mid p(x, y)\}$(方程组解集或曲线交点坐标)
有限集:含有有限个元素的集合,用 $\mathrm{card}(A)$ 来表示有限集合中元素的个数。如 $A = \{a, b, c\}$,则 $\mathrm{card}(A) = 3$。
容斥原理:
$\mathrm{card}(A \cup B) = \mathrm{card}(A) + \mathrm{card}(B) - \mathrm{card}(A \cap B) $
当且仅当 $A \cap B = \varnothing$ 时,
$\mathrm{card}(A) + \mathrm{card}(B) = \mathrm{card}(A \cup B)$
集合部分到此结束,题目练习如下:
1.已知全集 $ U = \{1, 2, 3, 4, 5\} $,集合 $ A = \{1, 2, 3\} $,$ B = \{2, 3, 4\} $。求:
(1)$ A \cup B $
(2)$ A \cap B $
(3)$ C_U A $(即 $ A $ 在 $ U $ 中的补集)
(4)$ (A \cup B) \cap C_U B $
2.设集合 $ A = \{x \mid x^2 - 3x + 2 = 0\} $,集合 $ B = \{x \mid x < 2\} $,求 $ A \cap B $。
3.已知全集 $ U = \mathbb{R} $,集合 $ A = \{x \mid x > 1\} $,$ B = \{x \mid x < 3\} $,求:
(1)$ C_U A $
(2)$ A \cup B $
(3)$ C_U (A \cap B) $
二. 函数,方程,不等式
等式与不等式
1. 若 a - b >0,则 $ a > b $;如果 a>b,则 a - b
2. 若 a - b = 0,则 a = b ;如果 a = b ,则 a - b = 0
3. 若 a - b < 0 ,则 a < b ;如果 a < b ,则 a - b < 0