数学

简谈高阶范畴论

欢迎纠错，LaTeX以后有时间补（我真的不会），主要我在网页端的LaTeX和板砖不一样

会慢慢补（？）hh

水贴愉快

发过，有人指出错误，已修改，重发一遍，感谢

换了科目（从物理到数学，毕竟数学的东西还是发在数学区更合适），致歉...

传统范畴论（Category Theory）通过对象（objects）和态射（morphisms）描述数学结构，其局限性在于仅能处理“相等”关系 而高等范畴论（Higher Category Theory）通过引入 n-态射（n-morphisms） 和 同伦相干性（homotopy coherence），将等式弱化为同伦等价，从而兼容拓扑、同伦代数与数学物理中的复杂结构

范畴论基础

范畴 C：由对象集合 Ob(C) 和态射集合 Hom_C(X,Y)（X,Y ∈ Ob(C)）构成，满足：

恒等态射：id_X ∈ Hom_C(X,X)

复合律：若 f ∈ Hom_C(X,Y), g ∈ Hom_C(Y,Z)，则 g∘f ∈ Hom_C(X,Z)

函子 F: C → D：将对象 X 映射为 F(X)，态射 f 映射为 F(f)，且 F(id_X)=id_F(X), F(g∘f)=F(g)∘F(f)

自然变换 η: F ⇒ G：对每个对象 X，给出态射 η_X: F(X)→G(X)，使得对任意 f: X→Y，有 η_Y ∘ F(f) = G(f) ∘ η_X

高等范畴

n-范畴（n-Categories）

2-范畴：在范畴基础上添加 2-态射（态射之间的变换）

例：

对象 X,Y；1-态射 f,g: X→Y；2-态射 α: f⇒g

复合操作：

纵向复合：2-态射 α: f⇒g 与 β: g⇒h 得 β∘α: f⇒h

横向复合：对 α: f⇒g 和 α': f'⇒g'，有 α'∗α: f'∘f ⇒ g'∘g

n-范畴：递归定义，包含 k-态射（1≤k≤n），且 k-态射可复合并满足相干条件

无穷范畴（∞-Categories）

定义：允任意维度的态射（k-态射，k∈ℕ），且所有高阶态射均可逆（同伦意义） 

例：

拓扑空间中的无穷范畴

对象：拓扑空间

1-态射：连续映射

2-态射：映射间的同伦 H_t: f≃g

3-态射：同伦之间的同伦（高阶同伦），以此类推

单纯集（Simplicial Sets）

定义：函子 Δ^op → Set，其中 Δ 是单形范畴（对象为有限序数 [n]={0,1,...,n}，态射为保序映射）

几何：将单纯集转化为拓扑空间，例如标准 n-单形 |Δ^n|

拟范畴（Quasi-Categories）

核心条件：对 0<k<n，任何态射 Λ^k_n → C 可延拓为 Δ^n → C，其中 Λ^k_n 是缺第 k 面的 n-单形

拟范畴是 (∞,1)-范畴的模型（所有 k-态射对 k>1 可逆）

例：

拓扑空间范畴可通过奇异单纯集构造为拟范畴

同伦极限与Kan扩张

同伦极限（Homotopy Limits）

传统极限要求图表严格交换，而同伦极限允许相差一个同伦

例：

同伦拉回：对空间映射 X→Z←Y，同伦拉回是空间 {(x,y,γ) | γ: f(x)≃g(y)}

通过单纯集或模型范畴中的导出函子实现

Kan扩张（Kan Extensions）

给定函子 F: C→E 和 K: C→D，左Kan扩张 Lan_KF: D→E 满足：

Lan_KF(d) = colim_(K↓d) F∘π（其中 π: (K↓d)→C 是遗忘函子）

同伦Kan扩张：在无穷范畴中，用同伦余极限替代余极限

导出几何（Derived Geometry）：

将代数几何中的概形推广为“导出概形”，其结构层是微分分次代数或单纯交换环

拓扑量子场论（TQFT）：

扩展的Cobordism范畴是 2-范畴，其对象为流形，1-态射为配边，2-态射为配边之间的微分同胚

同伦类型论（Homotopy Type Theory）：

将无穷范畴与类型论结合，其中“等词类型”对应同伦纤维化

模型范畴：（同伦理论的范畴化基石）

模型范畴的定义与公理

一个模型范畴 $\mathcal{M}$ 包含三类态射：

弱等价（Weak Equivalences）：记为 $\overset{\sim}{\to}$，传递同伦信息

纤维化（Fibrations）：提升性质对应“纤维化”结构

上纤维化（Cofibrations）：对偶概念

公理系统：

完备性与上完备性（极限与余极限存在）

二选三性质：若 $f\circ g$ 与 $f$ 是弱等价，则 $g$ 亦然

提升性质：对图示

· → · ↓ ↓ · → ·

若竖直一边为上纤维化且另一边为纤维化，且至少一边为弱等价，则存在提升

单纯集模型范畴

对象：单纯集 $S_\bullet$

弱等价：几何实现后的同伦等价

纤维化：Kan纤维化（所有 horn 可扩张）

上纤维化：单射态射

此模型结构使 $sSet$ 成为 $\infty$-范畴的标准载体。

∞-范畴的局部化与可表现理论

局部化构造

对范畴 $\mathcal{C}$ 与子集 $W\subset Mor(\mathcal{C})$，∞-局部化 $L: \mathcal{C}\to \mathcal{C}[W^{-1}]_\infty$ 满足：

将 $W$ 中态射变为等价

对任意 ∞-范畴 $\mathcal{D}$，函子 $\mathcal{C}\to\mathcal{D}$ 将 $W$ 映为等价当且仅当通过 $L$ 唯一因子化

可表现∞-范畴

类比 locally presentable 范畴，∞-范畴 $\mathcal{C}$ 可表现需满足：

余完备

由小生成子生成

滤余极限与有限极限交换

例：

拓扑空间 ∞-范畴、链复形导出 ∞-范畴

导出代数几何的范畴基础

导出概形

一个导出概形 $(X,\mathcal{O}_X)$ 包含：

拓扑空间 $X$

结构层 $\mathcal{O}_X$ 取值于 微分分次代数（DGAs） 或 单纯交换环

其 无穷范畴结构 的体现：

截面 $\Gamma(U,\mathcal{O}_X)$ 不是普通环，而是 DG-代数/单纯环

态射空间 $\mathbf{Map}((X,\mathcal{O}_X),(Y,\mathcal{O}_Y))$ 是 ∞-群胚

刚性提升定理

对于拉回图

X' → X ↓ ↓ Y' → Y

在导出几何中，若竖直箭头为平坦态射，则拉回不仅是同伦拉回，且保持 导出光滑结构

数学物理中的高阶范畴模型

扩展拓扑量子场论

一个 $n$-维 TQFT 是 $n$-范畴间的对称幺子函子：  $$Z: \mathbf{Bord}_n^{fr} \to \mathcal{C}$$其中：

$\mathbf{Bord}_n$：对象为 $(n-1)$-流形，1-态射为 $n$-维配边，2-态射为配边间的微分同胚，以此类推至 $n$-态射

$\mathbf{Vect}_\mathbb{C}^{(n)}$：$n$-范畴版本的复向量空间范畴

缺陷算子范畴

在共形场论中，缺陷算子 形成 融合范畴：

对象：拓扑缺陷线

1-态射：缺陷上的局部算子

2-态射：算子乘积

其数学实现通过 模张量范畴 $\mathcal{M}$，满足融合规则： $$\dim(\mathcal{M}) = \sum_i d_i^2$$ 其中 $d_i$ 是简单对象量子维数

同伦类型论与∞-范畴的对应

类型论解释

在 同伦类型论（HoTT） 中：

类型 $A$ 解释为 ∞-群胚

项 $a:A$ 解释为对象

相等类型 $a=_A b$ 解释为路径空间 $\mathbf{Map}_A(a,b)$

高阶代数簇的 ∞-范畴刻画：通过导出栈理论重构模空间

范畴量子霍尔效应：利用 monoidal ∞-范畴描述拓扑序

导出 Langlands 纲领：将自守形式范畴视为 ∞-范畴的纤维积

高等范畴论正从“元语言”逐步转变为具体数学物理问题的计算工具

会有查阅资料和搜索的补充和确认，比如前沿和物理方面等

模型范畴论的精细构造

模型范畴的公理体系

设 $\mathcal{M}$ 为具有有限完备与上完备的范畴，其模型结构由三族态射 $(Cof, Fib, Weq)$ 组成，满足：

提升公理：对任意（非严格）交换图

A → X i↓ ↓p B → Y

若 $i \in Cof$ 且 $p \in Fib$，且满足 $i \in Weq$ 或 $p \in Weq$，则存在提升 $h: B → X$ 使两三角交换

因子化公理：任意态射 $f$ 可因子化为：

(1) $f = p \circ i$，其中 $i \in Cof \cap Weq$，$p \in Fib$

(2) $f = q \circ j$，其中 $j \in Cof$，$q \in Fib \cap Weq$

单纯集模型范畴的具体实现：

对象：$\Delta^{op} \to \mathbf{Set}$ 的函子

弱等价：诱导几何实现同伦等价的态射

上纤维化：单形态射（逐项单射）

纤维化：Kan纤维化，即对任意 horn 包含 $\Lambda^k_n \hookrightarrow \Delta^n$ 具有右提升性质

模型范畴的局部化理论

给定模型范畴 $\mathcal{M}$ 与子集 $S \subset Mor(\mathcal{M})$，可通过 Bousfield 局部化构造新模型范畴 $L_S\mathcal{M}$，其中：

弱等价扩张为 $S$-局部等价

纤维化变为 $S$-局部纤维化

局部对象满足：对任意 $f: A→B \in S$，诱导映射 $\mathbf{Map}(B,X) \overset{\sim}{\to} \mathbf{Map}(A,X)$

计算实例：拓扑空间的局部化 $L_n\mathbf{Top}$，其中 $S = {K(G,n) \to *}$，对应 $n$-截断同伦理论

∞-范畴的严格化模型

拟范畴的组合定义

一个拟范畴是单纯集 $C_\bullet$，满足对任意 $0 < k < n$，任何映射 $\Lambda^k_n \to C$ 可延拓为 $\Delta^n \to C$

态射空间的同伦结构： 对对象 $x,y \in C_0$，定义映射空间 $\mathrm{Map}_C(x,y)$ 为单纯集： $\mathcal{O}_X \in \mathbf{Shv}_{\mathcal{Comm}(\mathcal{S})}(X)$

完备∞-范畴理论

定义：∞-范畴 $\mathcal{C}$ 称为可表现的当且仅当：

存在正则基数 $\kappa$，使得 $\mathcal{C}$ 由 $\kappa$-紧对象生成

$\mathcal{C}$ 具有所有小余极限

$\kappa$-滤余极限与有限极限交换

米田嵌入的∞-版本： $$j: \mathcal{C} \hookrightarrow \mathcal{P}(\mathcal{C}) = \mathbf{Fun}(\mathcal{C}^{op}, \mathcal{S})$$ 其中 $\mathcal{S}$ 为空间∞-范畴（∞-群胚范畴）

高阶代数几何的范畴基础

导出概形的严格定义

一个导出概形 $(X, \mathcal{O}_X)$ 包含：

拓扑空间 $X$

结构层 $$\mathrm{Map}_C(x,y)_n = \left\{ f: \Delta^n \to C \mid f|_{v_0} = x,\ f|_{v_n} = y \right\}$$取值于交换代数∞-范畴

切复形的∞-描述： 对点 $x: \mathrm{Spec}(k) \to X$，切复形 $\mathbb{T}X$定义为拉回：

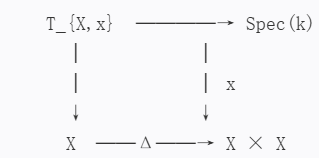
导出叠的∞-范畴结构

一个导出 Artin 叠是∞-函子 $\mathcal{F}: \mathcal{Comm}(\mathcal{S})^{op} \to \mathcal{S}$，满足：

在 Etale 拓扑下是层

对角线 $\mathcal{F} \to \mathcal{F} \times \mathcal{F}$ 是 $(n-1)$-几何的

存在光滑 n-图册 $U \to \mathcal{F}$

数学物理中的严格范畴模型

拓扑量子场论的完整定义

一个 n-维完全扩展 TQFT 是 symmetric monoidal (∞,n)-函子： $$Z: \mathbf{Bord}_n^{fr} \to \mathcal{C}$$ 其中 $\mathbf{Bord}_n^{fr}$ 为 framed n-维配边∞-范畴：

对象：framed 0-流形

1-态射：framed 1-维配边

k-态射：framed k-维配边间的映射

缺陷算子范畴的融合规则

设 $\mathcal{C}$ 为 unitary modular tensor category，其融合规则满足： $$\mathrm{Hom}(X \otimes Y, Z) \cong \bigoplus_{W \in \mathrm{Irr}(\mathcal{C})} N_{XY}^W \otimes \mathrm{Hom}(W,Z)$$

其中融合系数 $N_{XY}^W = \dim \mathrm{Hom}(X \otimes Y, W)$ 满足 Verlinde 公式： $$N_{ij}^k = \sum_m \frac{S_{im}S_{jm}S_{km}^*}{S_{0m}}$$

高阶规范理论的∞-范畴描述

对于李群 $G$ 的规范理论，构型空间为： $$\mathcal{M} = \mathbf{Map}(M, BG)$$ 其中 $BG$ 视为具有单对象的∞-群胚，其映射空间给出主 G-丛的模空间

同伦类型论的范畴语义

Voevodsky 宇宙层级的严格处理

在类型论中假设宇宙序列 $\mathcal{U}_0 : \mathcal{U}_1 : \mathcal{U}_2 : \cdots$，对应∞-范畴中的对象分类器：

分类定理：对任何∞-范畴 $\mathcal{C}$，存在自然等价：$$\mathrm{Fun}(\mathcal{C}, \mathcal{S}) \simeq \mathrm{PSh}(\mathcal{C}) = \{\mathcal{C}^{\mathrm{op}} \to \mathcal{S}\}$$

高阶归纳类型的∞-解释

考虑圆环类型 $S^1$ 作为高阶归纳类型：

构造函数：$\mathrm{base} : S^1$, $\mathrm{loop} : \mathrm{base} = \mathrm{base}$

其语义解释为单纯集模型中的几何圆环 $|S^1| \simeq S^1$

消去规则：对任何类型族 $P : S^1 \to \mathcal{U}$，给定：

$b : P(\mathrm{base})$

$l : \mathrm{transport}^P(\mathrm{loop}, b) = b$

则存在截面 $\prod_{x:S^1} P(x)$

导出Langlands纲领的∞-范畴重构

设 $G$ 为约化群，考虑对应： $$\mathbf{Shv}_{\mathcal{D}(k)}(\mathrm{Bun}_G) \rightleftharpoons \mathbf{QCoh}(\mathrm{Loc}_{{}^LG})$$

其中 $\mathbf{QCoh}$ 为拟凝聚层∞-范畴，$\mathcal{D}(k)$ 为微分分次代数范畴

动机上同论的∞-范畴模型

Voevodsky 动机范畴 $\mathbf{DM}(k)$ 可构造为： $$\mathbf{DM}(k) = \mathbf{Shv}_{\mathbf{A}^1, \mathrm{Nis}}(\mathbf{Sm}_k)[\mathbb{W}^{-1}]_\infty$$

其中 $\mathbb{W}$ 为适当弱等价类

稳定同伦范畴的无穷局部化：$\mathbf{SH}(k)[\rho^{-1}]_\infty$ 的显式构造

高阶TQFT的分类空间：$\mathbf{Bord}_n$ 的 Postnikov 塔描述

导出叠的无限层结构：导出 Artin 叠的层级分类定理

我不行了，这个补充不查点资料真写不出来...还有这个LaTex真是要命...我不行了...