物理
以三维之躯，窥视四维时空？

丨丨长江东逝水(´･v･)ﾉ更新于2025-11-25 08:58:03

适用轮次：基础轮＋

隶属于：立体几何+数列

(´^^)ﾉﾉ

现在我们注意这样一个问题：平面上n条直线最多可以把平面分成几个部分？

这个问题并不难解决：我们设平面上n条直线最多可以把平面分成${A}_{n}$个部分

注意到，平面内一条直线最多只能把平面分成两个部分，两条直线四个部分，即${A}_{1}$＝2，${A}_{2}$＝4，这是显而易见的

但是当直线数增加到第三条时，问题开始变得有趣了：我们注意到第三条直线与前两条直线最多产生两个交点，这两个交点能把该直线分成三个部分；在这三个部分的内侧，原先平面的四个部分依旧存在，但在这三个部分的外侧，平面又往外延伸出了三个部分

（如图）

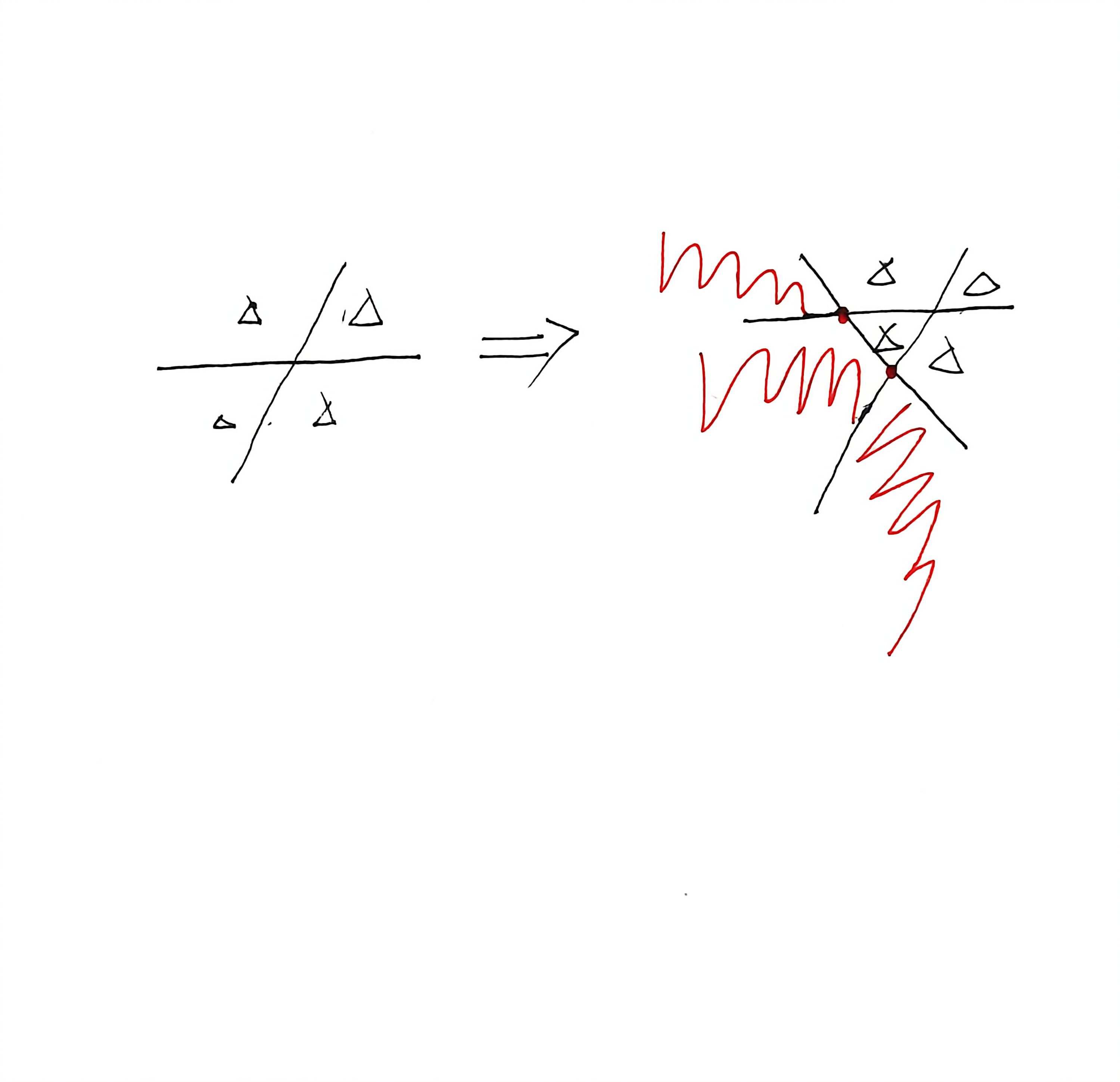
所以三条直线最多能把平面分成${A}_{2}$+3=7个部分，即${A}_{3}$=${A}_{2}$+3

同理，加入第四条直线会与前三条直线最多产生三个交点，这三个交点把第四条直线分成四部分；四个部分以内，原先7个部分依旧存在；四个部分以外分别往外延伸出四个部分。

所以我们有${A}_{4}={A}_{3}+4$

同理，我们可以获得${A}_{n}$的递推公式：${A}_{n}={A}_{n-1}+n$，其中${A}_{1}=2$

由此求得通项公式：${A}_{n}=\frac{n^2+n+2}{2}$

现在我们再来更深入的思考一点，提升一个维度：空间中n个平面最多可以把空间分成几个部分？

它的解决方法是类似的：我们设空间中n个平面最多可以把空间分成${B}_{n}$个部分

则易有${B}_{1}=2$，${B}_{2}=4$

加入第三个平面后，它会与前两个平面最多产生两条交线，这两条交线最多能把平面分成四个部分，在这四个部分以内，原先的四个部分保留；在这四个部分以外，空间会向外拓展出四个部分（这需要一点空间想象力）

（如图）

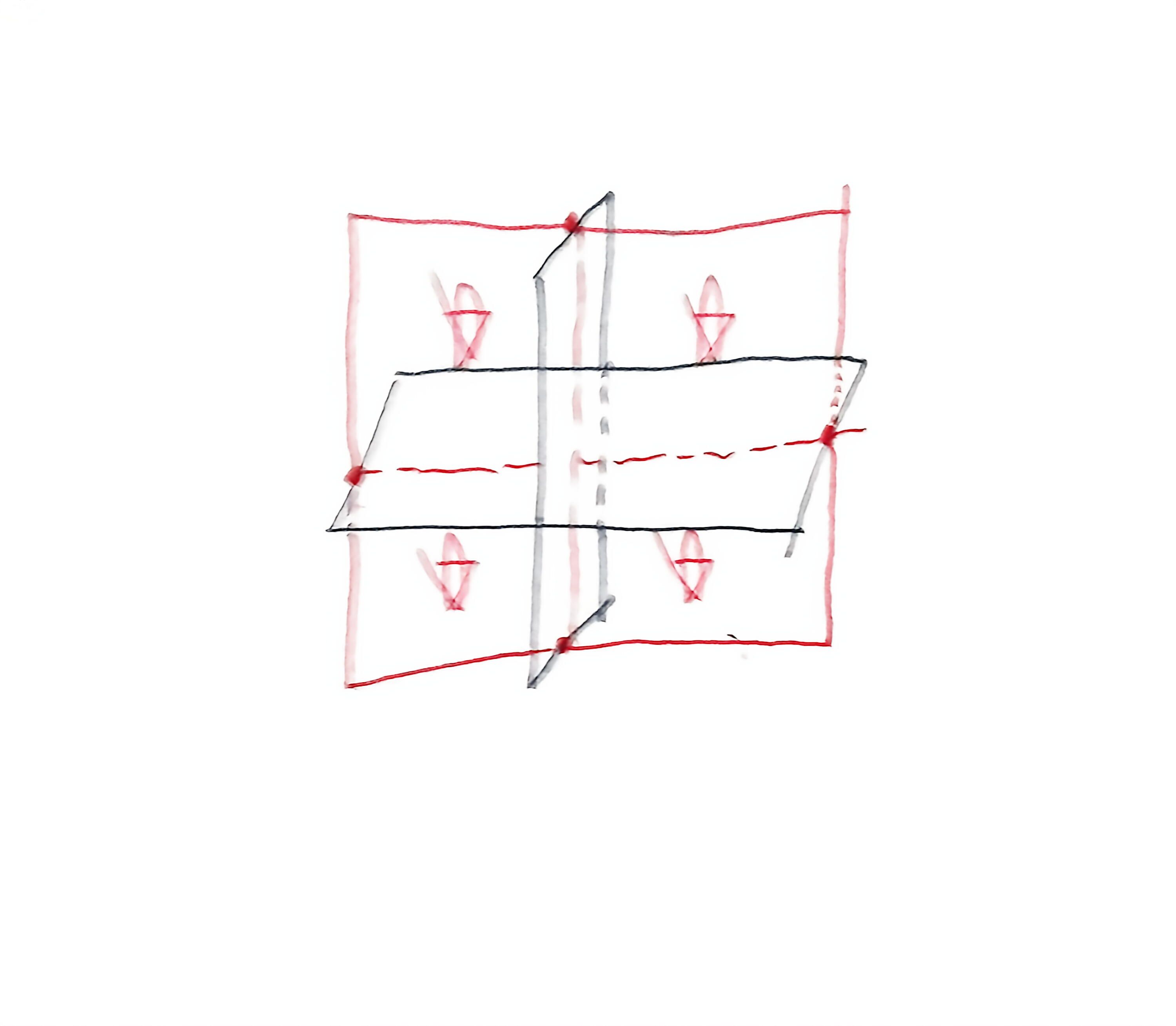
所以我们可以得到${B}_{3}={B}_{2}+4$，我们又注意到这里的四其实就是${A}_{2}$，

所以有：${B}_{3}={B}_{2}+{A}_{2}$

同理，${B}_{4}={B}_{3}+{A}_{3}$，${B}_{5}={B}_{4}+{A}_{4}$......

所以我们可以得到该递推公式：${B}_{n}={B}_{n-1}+{A}_{n-1}$，即${B}_{n}={B}_{n-1}+\frac{n^2-n+2}{2}$，其中${B}_{1}=2$

由此求得通项：${B}_{n}=\frac{n^3+5n+6}{6}$

现在让我们不妨再大胆一些，把维度提升到四维（这里只考虑空间维度，不考虑时间维度）

按照上面的经验，我们依旧可以求出N个三维空间最多能把四维空间分成几部分...吗？

其实是不行的，因为它有一个致命的缺陷：上面的方法是由先求出递推，再求通项的，但是我们并不知道四维递推公式的首项是什么----即我们三维的大脑不知道一个三维空间可以把四维空间分成几部分这个初始值！这也就是为什么我在标题中会加一个问号

所以以下内容是完全没有数学依据的，仅供学术娱乐：

因为一个零维的点可以把一维线分成两部分；一个一维的线可以把二维平面分成两部分；一个二维平面可以把三维空间分成两部分，所以我们不妨大胆猜测：一个三维空间可以把四维空间分成两部分

有了这个初始条件之后，我们就可以用与上面相同的方法求得了，这里给出答案：

若设为${C}_{n}$,则${C}_{n}=\frac{n^4-2n^3+11n^2+14n+24}{24}$，读者自证不难（）

用这种方法，在默认初始值为二的情况下，其实还可以求出q个p-1维空间最多能把p维空间分成几部分，但毕竟没有数学依据，只是学术娱乐，再往下推就没意思了，故在此不过多赘述，有兴趣的读者可以自己探索

时空行为 O-Box

收起

共10条回复

ricky-大号已似

1月前

感觉很久以前看到过你......这个有啥用？是意味着我们可能切割存在于弦论之中的10/26维空间吗

9条评论

丨丨长江东逝水(´･v･)ﾉ

1月前

很久以前看到过我正常，来挺久了

要说有啥用，以目前的基础理学理论来说肯定是不知道的，但或许在将来的某一天能帮助我们三位的大脑思考高维空间（）

ricky-大号已似 回复 丨丨长江东逝水(´･v･)ﾉ

1月前

那么可能只能等升维了.....不然没有亲身经历不可能理解高维空间，或者去找翘曲点？现在进翘曲点应该算找死吧，毕竟不能在开放空间生成大气，那看来可能要好久了

ricky-大号已似 回复 丨丨长江东逝水(´･v･)ﾉ

1月前

那么问题又来了，现在我们应该思考更深层次的万物理论还是更实际的应用物理，寻找一个大统一理论的意义在哪里？是为了更好的研究现实吗？那么现在的理论也拟合得很好，除了有点丑，而大统一理论总是有很苛刻的条件，真的有必要寻找更“美”的大统一理论吗

丨丨长江东逝水(´･v･)ﾉ 回复 ricky-大号已似

1月前

还是那句话嘛，你得知道物质是由原子组成的，才能造出原子弹，否则你就只能一直在那改造你的弓箭长矛

当然改造弓箭长矛也是很重要的，但探索物质规律才是本质

ricky-大号已似 回复 丨丨长江东逝水(´･v･)ﾉ

1月前

但是这个“美”的理论在现实中不存在，比如杂化弦，可以统一四大基本力，60多种（？）基本粒子，在普朗克能量的情况下才能实现，对于实际有什么用呢？难道你要把整个仙女星系能量化，然后就为了验证一个理论向真空输入一大堆无用的热能？这也是不现实的可以探索，但这种只能存在于理论，就好像你用688号元素造原子弹，行吗？理论行，真能吗？你有吗？只能说过度的探索是无义的。

我先下了，过会看看能不能上