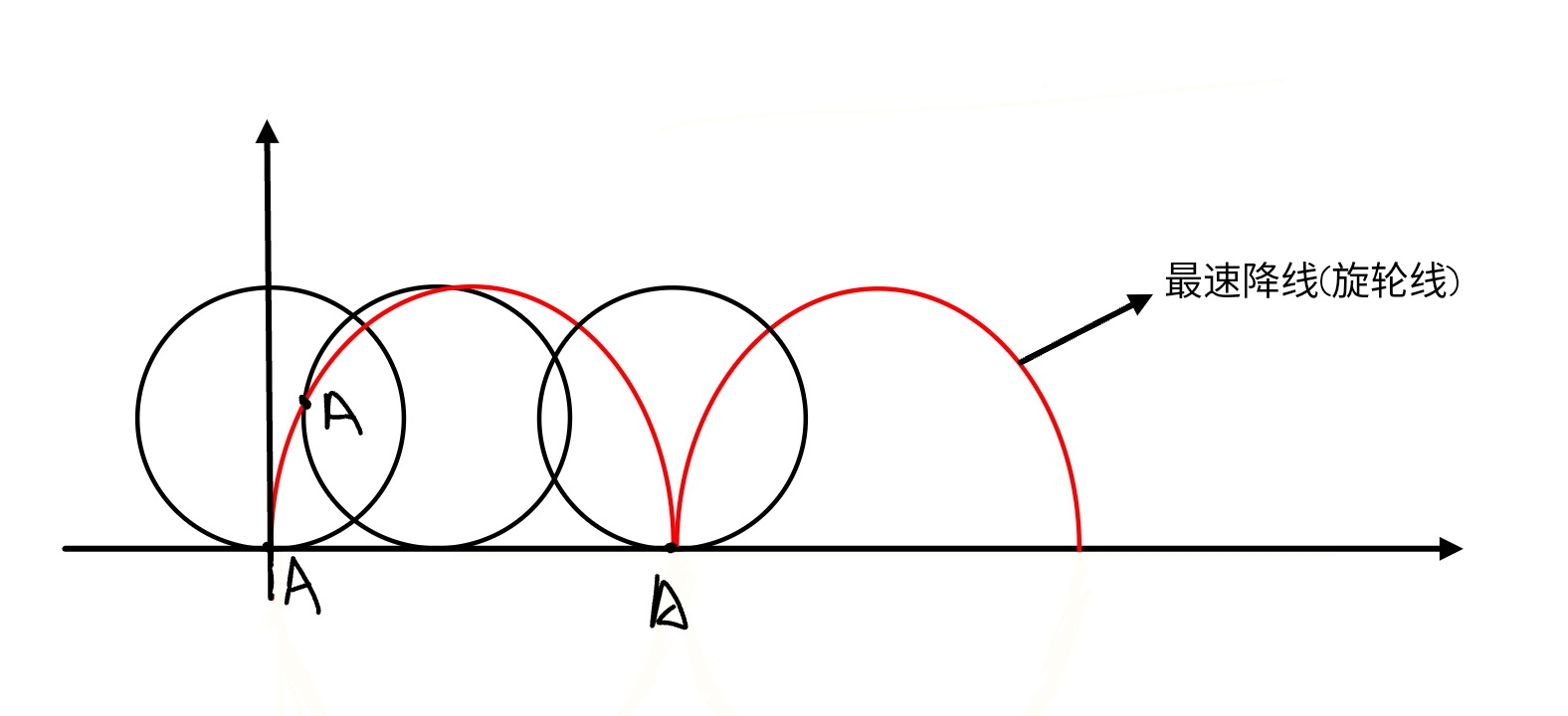
物理

从折射定律到最速降线

在初中阶段我们学习过光的折射，并研究了凸透镜的成像，有深入了解过的朋友都知道光的折射定律：n=sinθ₁/sinθ₂

那么它(她)是怎么来的呢？下面我们来导一下(这倒是提醒我了)

根据费马原理，光总是沿光程(光的🦌程)取极值的方向传播，于是我们作如下草图：

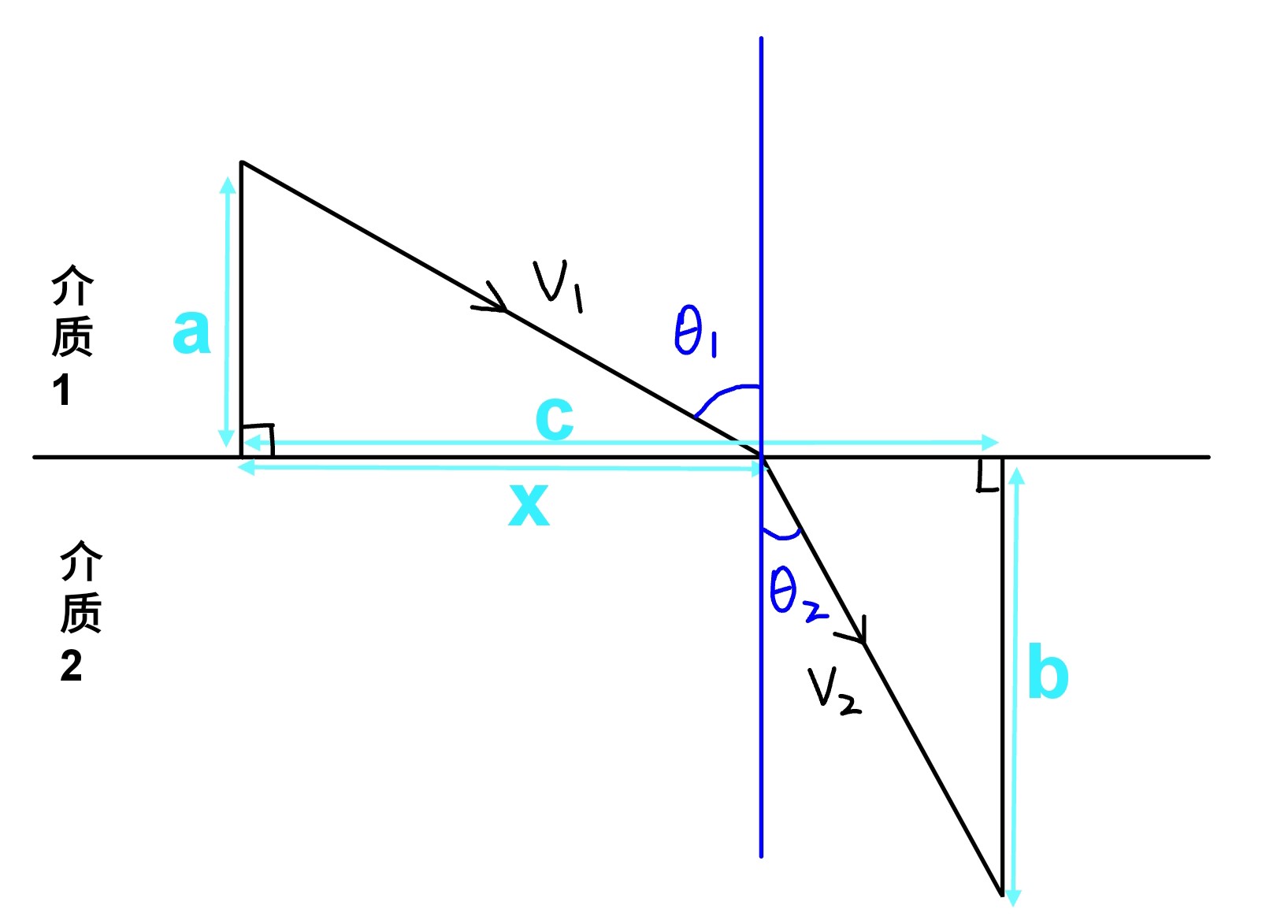
其中v₁，v₂分别为光在介质1和介质2中的传播速度(假定两介质不相同)

于是我们可得光经过两段斜线所需时间t与x的函数关系为(a，b，c为常量)

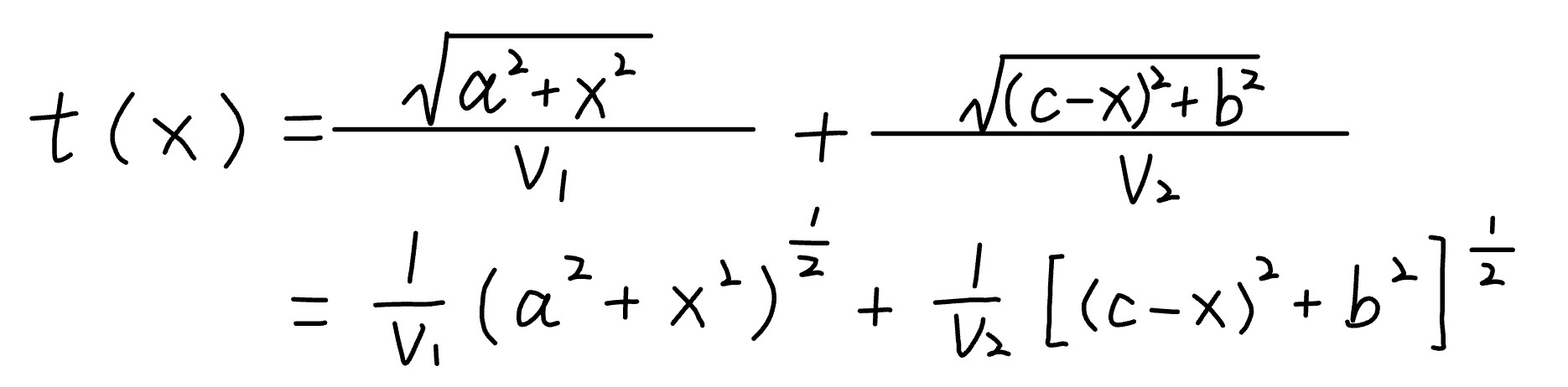
t对x求导得

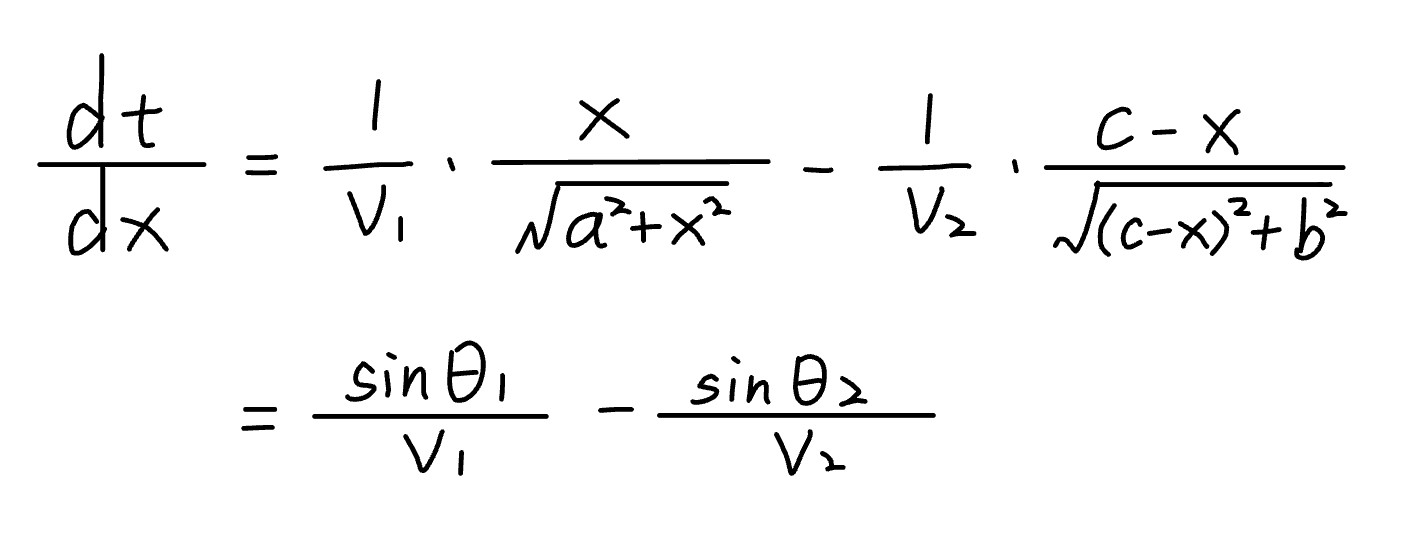
取极值时dt/dx=0，故有sinθ₁/v₁=sinθ₂/v₂

∵sinθ/v=C(其中C为常数)，n=v/c  ∴n=sinθ₁/sinθ₂

证毕

肥肠简单对吧，下面我们来看一个与它有异曲同工之妙的问题——最速降线

什么是最速降线呢？它说的是这样一件事:

我们都知道如果斜面摩擦力不大且小球受重力足够，那么它就会从斜面上滚下来，且当起始点与终点相同时，斜面的曲度会影响它下落的时间

而能使小球最快滚下的那条曲线就被称为最速降线

求解过程如下：

显而易见的，最速降线应该是一条“向下凹”的曲线，我们先随手画个草图

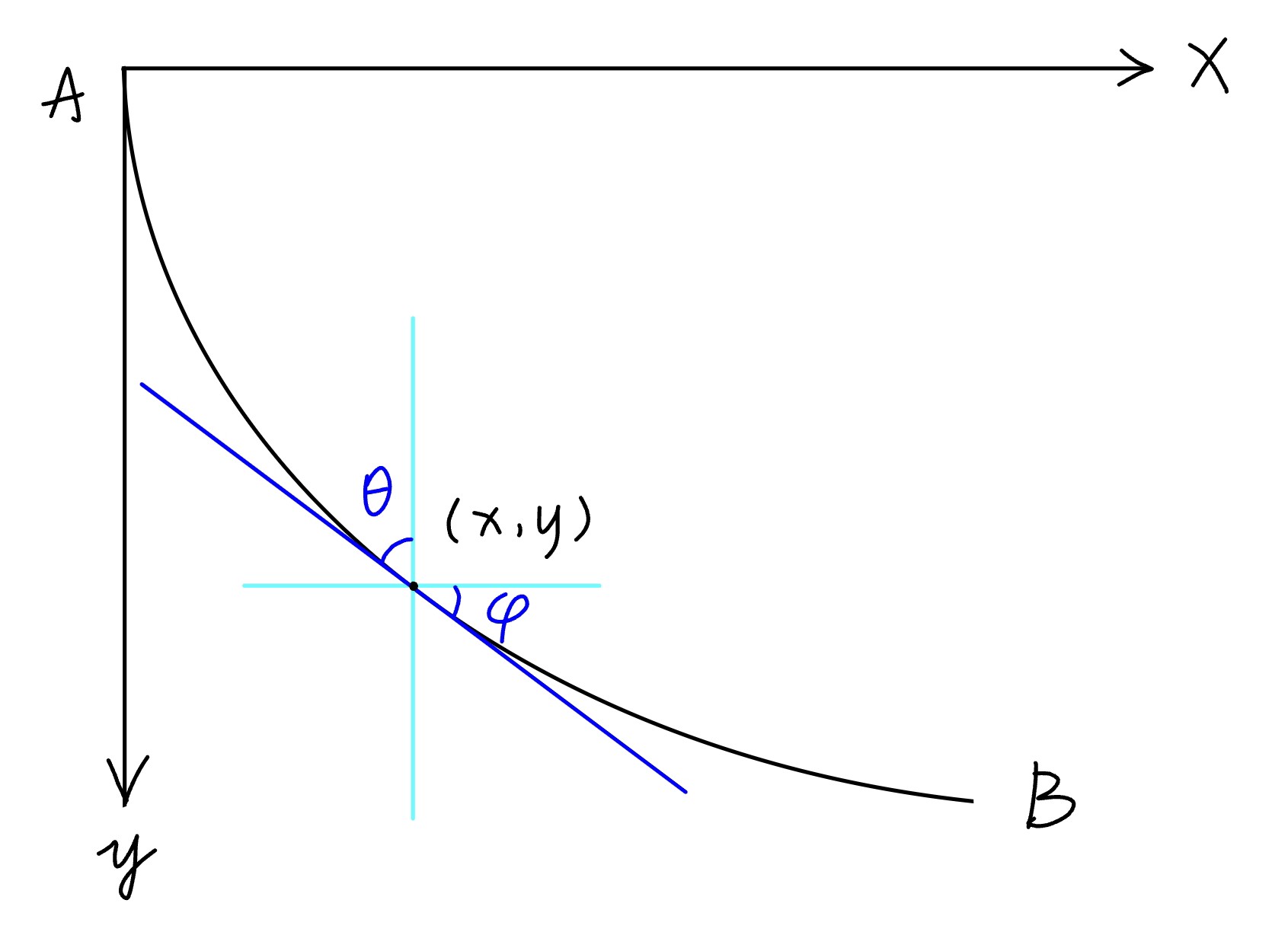
取曲线上任意一点(x,y)，作该点的切线，切线与x轴，y轴的夹角分别为φ,θ(为了更加直观，图中浅蓝色线是将轴经过平移得到，角的位置有变但大小不变)

设小球质量为m，重力加速度(重力常数)为g，且小球视为质点

根据动能定理，竖直方向上有：

mg·y=mv²/2  ⇒  v=√(2g·y)

又有θ+φ=π/2(弧度制)  ⇒  sinθ=cosφ=1/√(1+tan²φ) (这里运用了三角恒等变换)

其中tanφ为切线斜率，即tanφ=dy/dx=y'(依旧导数)

由上文我们类推：sinθ/v=C(C为常数，与上文C无关系)

带入sinθ与v得：(1+y'²)y=C  ⇒  y'=√[(C-y)/y]

化为比较简洁的微分方程(说人话就是把y'拆开(y',自己掰开！)然后把dx单独移到一边)

我们得到：dx=√[y/(C-y)]·dy

直接解显然有点难办(难办就别办辣！)，于是我们想到，令y=C·sin²t(注意力惊人)

然后我们就有：

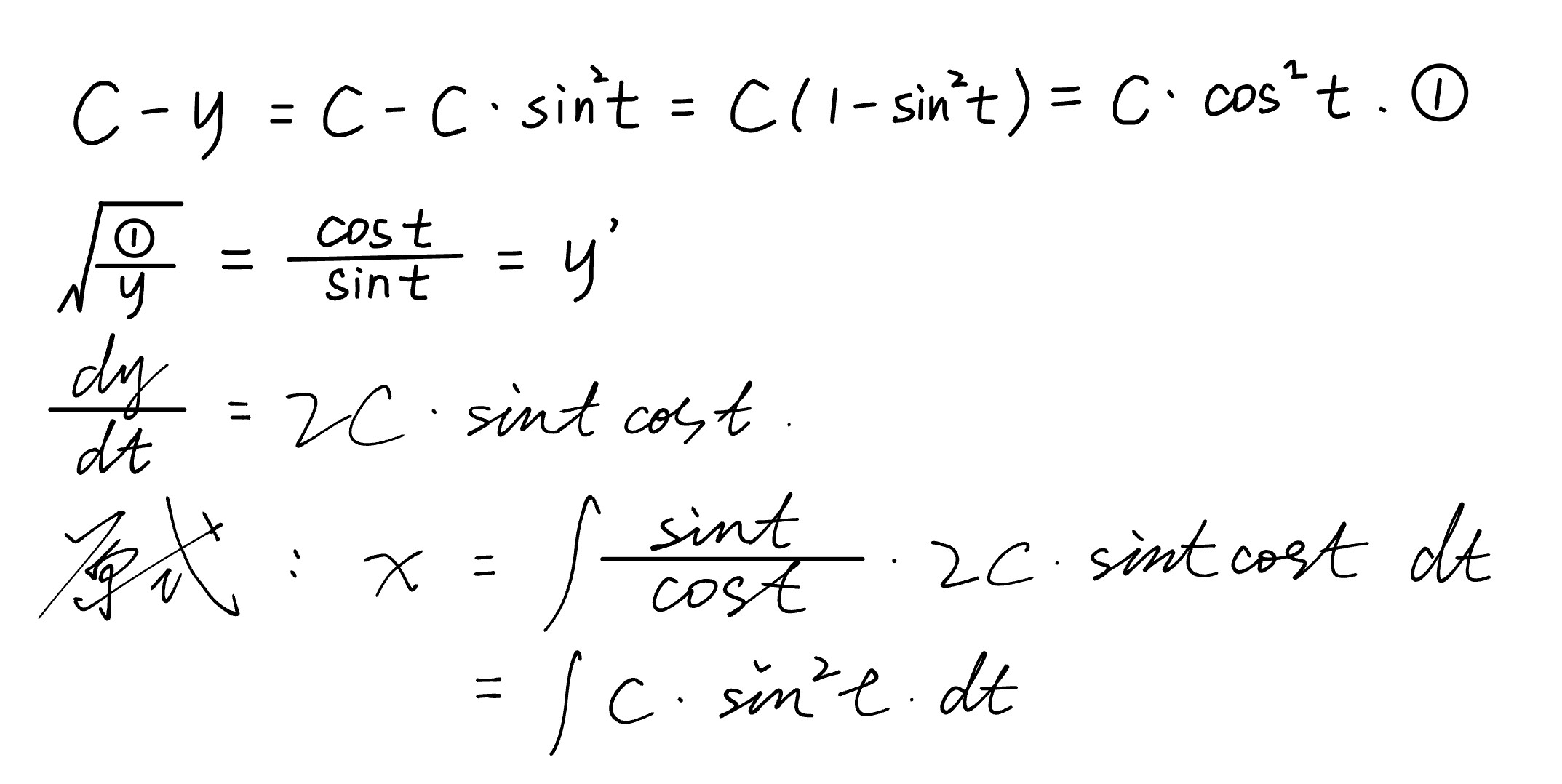
根据二倍角公式以及三角恒等变换：

cos2t=cos²t-sin²t=1-2sin²t

代入上式：

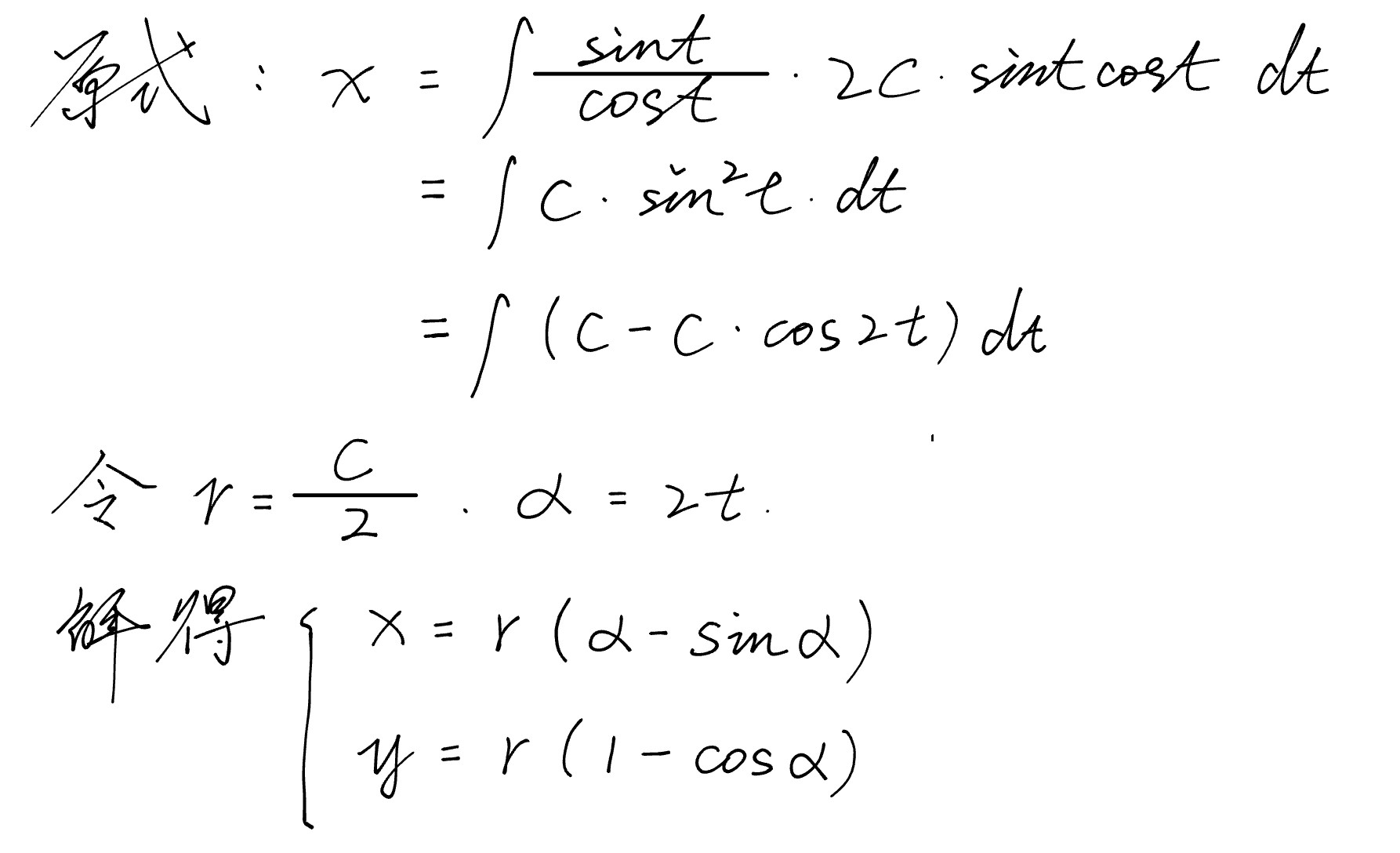
可见，结果是个方程组，

那么这个东西到底是什么呢

其实就是一个圆沿直线滚动形成的曲线(的对称线)，称为旋轮线(摆线)

在这里感谢由@云游于宇宙边际的浮游生物提供的函数图像

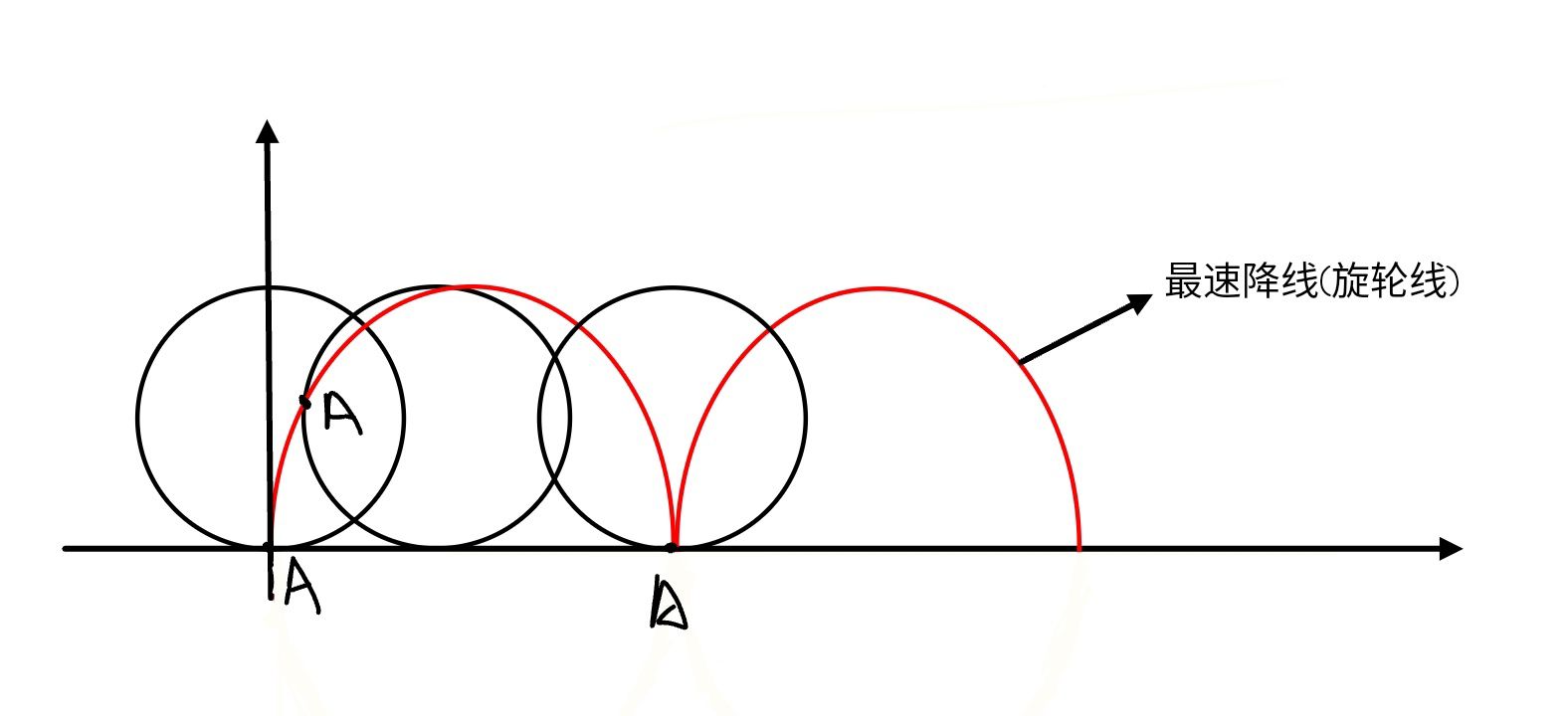
将数据标注在上图，我们得到：

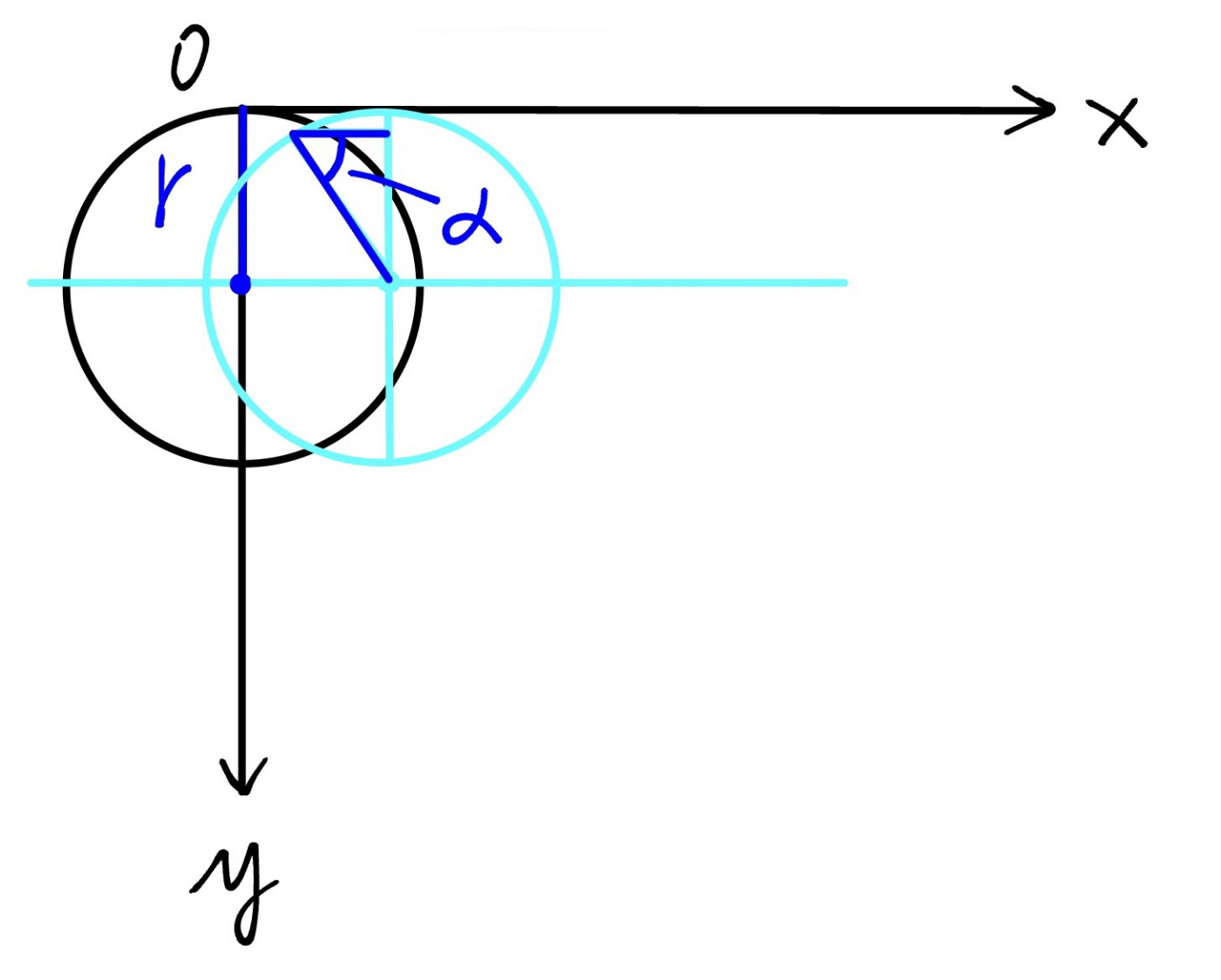
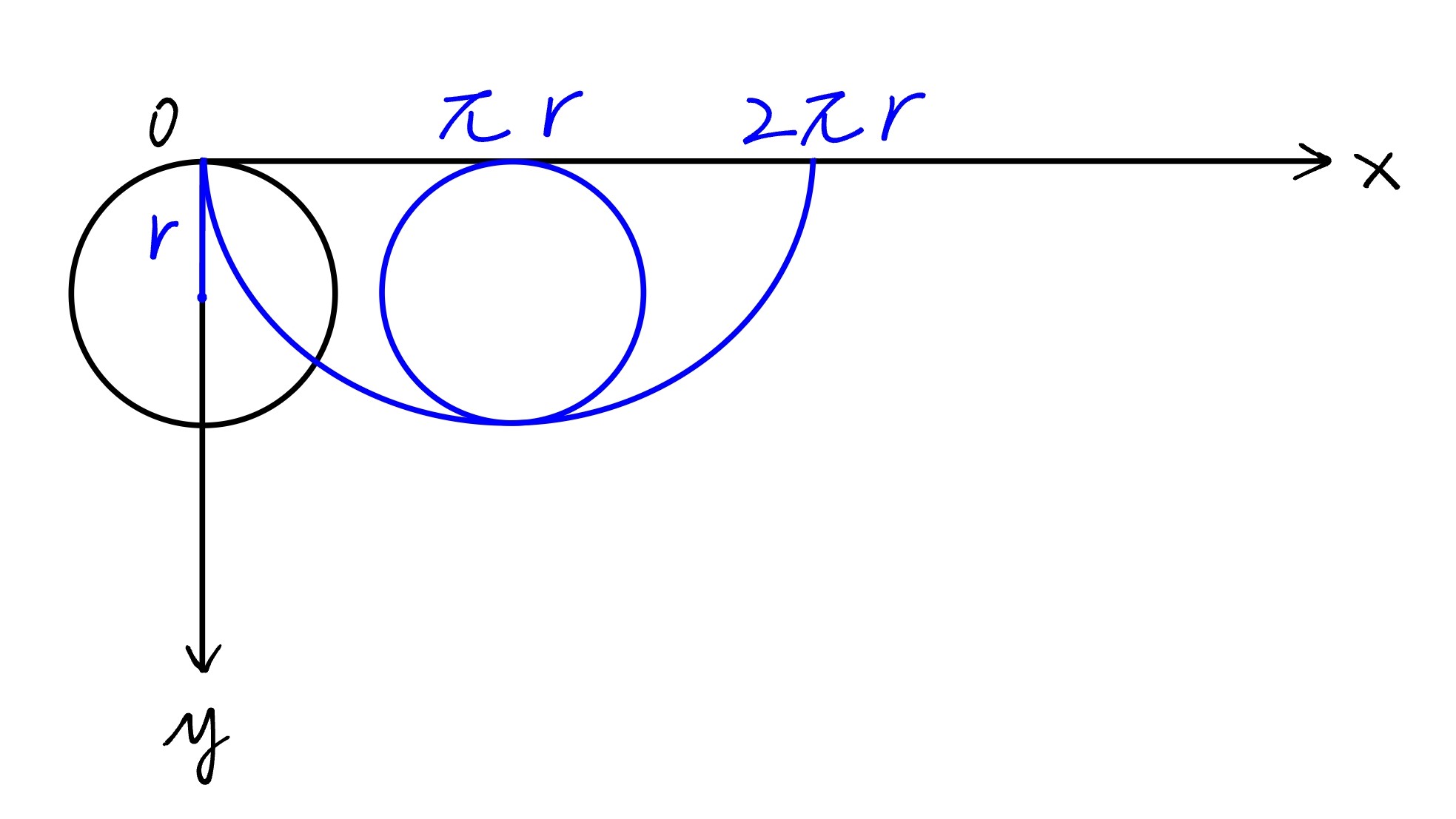
可见在上述参数方程组中，r实际上是所旋转的圆的半径，α为该半径所经过的弧度角

至此最速降线证毕

完结撒花，感谢陪伴

注：该帖由@云游于宇宙边际的浮游生物提供作图与思路支持，她(酒石股亦滴)的帖子有更加严谨的证明，如有需要请移步，感谢配合

        感谢@麓鸣与@florr——24zhao提供思路与资料支持

另：如有错误，感谢各位佬指出