物理

菲涅尔积分

哭死，全卡没了，施工中

一、定义

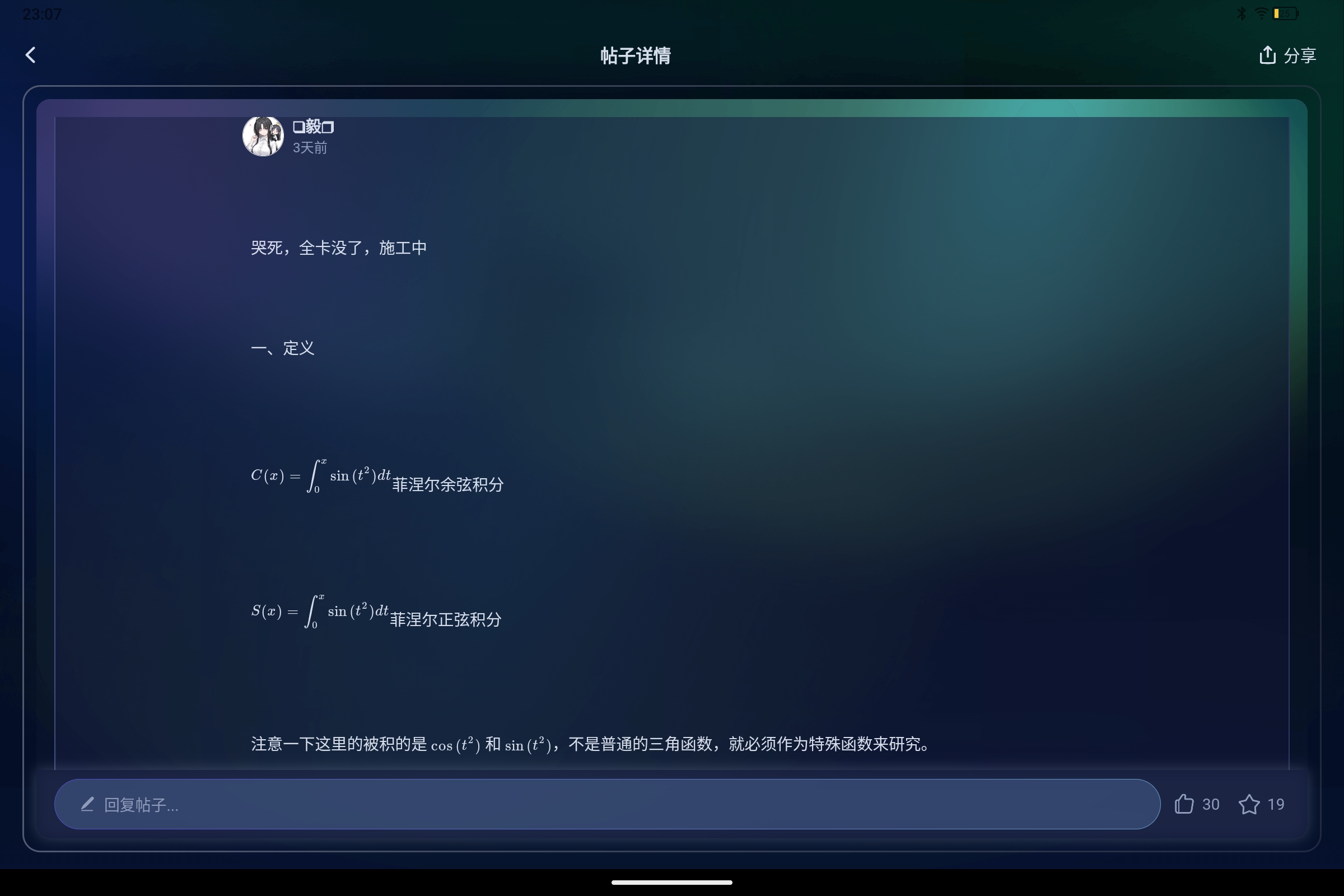
$C(x)=\int_0^x\sin(t^2) dt$菲涅尔余弦积分

$S(x)=\int_0^x\sin(t^2)dt$菲涅尔正弦积分

注意一下这里的被积的是 $\cos(t^2)$ 和 $\sin(t^2)$，不是普通的三角函数，就必须作为特殊函数来研究。

一个法国物理学家,叫 奥古斯丁·让·菲涅尔的（Augustin-Jean Fresnel），他在19世纪研究光的衍射现象时首次系统地使用了这类积分。他发现当光通过狭缝或绕过障碍物时，其传播可以用这些积分来描述，因此叫这个名字。

性质与图像

 1. 函数行为

 当 $x \to 0$ 时：

  

  $C(x) \approx x - \frac{x^5}{5 \cdot 3!} + \cdots,\quad S(x) \approx x - \frac{x^5}{5 \cdot 3!} + \cdots$

 

  所以 $C(0) = S(0) = 0$

- 当 $x \to \infty$ 时：

 

  $\lim_{x \to \infty} C(x) = \int_0^\infty \cos(t^2)\,dt = \sqrt{\frac{\pi}{8}}$

  $\lim_{x \to \infty} S(x) = \int_0^\infty \sin(t^2)\,dt = \sqrt{\frac{\pi}{8}}$

这两个极限值后面会推导.

2.  图像的话函数 $C(x)$ 和 $S(x)$ 都是连续、光滑且单调递增的（在某些区间振荡增长），从上面可看出最终趋于收敛。

简单描述就是呈现出“振荡趋近”的趋势。

 它们在 x > 0 上缓慢增加，每经过一个“周期”（大约 $t^2 = (n+1/2)\pi$），函数值会震荡一次。

最终趋于常数 $\sqrt{\pi/8} \approx 0.6267$

下面开始上难度

复数形式与欧拉公式

我们可以将两个积分合并成一个复数积分：

$F(x) = C(x) + iS(x) = \int_0^x e^{i t^2}\,dt$

(复数形式)

进一步，考虑从 $0$ 到 $\infty$ 的积分：

$\int_0^\infty e^{i t^2}\,dt$

可以通过复变函数方法

有一个经典结果：$\int_0^\infty \cos(t^2)\,dt = \int_0^\infty \sin(t^2)\,dt = \sqrt{\frac{\pi}{8}}$

推导

失败思路（利用高斯积分和复分析）

考虑如下积分：

$I = \int_0^\infty e^{i t^2}\,dt$

令 $u = t^2$，则 $t = \sqrt{u}$，$dt = \frac{1}{2\sqrt{u}} du$，但这不好算。

呃呃呃，那就开大，用复平面上的围道积分

考虑：

$J = \int_0^\infty e^{-a t^2}\,dt = \frac{1}{2} \sqrt{\frac{\pi}{a}}$实数a>0

现在令 $a = -i$，即：

$\int_0^\infty e^{-i t^2}\,dt = \frac{1}{2} \sqrt{\frac{\pi}{-i}} = \frac{1}{2} \sqrt{\pi} \cdot (-i)^{-1/2}$

注意：$-i = e^{-i\pi/2}$，所以 $(-i)^{-1/2} = e^{i\pi/4} = \frac{1+i}{\sqrt{2}}$

$\int_0^\infty e^{-i t^2}\,dt = \frac{1}{2} \sqrt{\pi} \cdot \frac{1+i}{\sqrt{2}} = \sqrt{\frac{\pi}{8}} (1 + i)$

取共轭可得：

$\int_0^\infty e^{i t^2}\,dt = \sqrt{\frac{\pi}{8}} (1 - i)$

但注意：我们想要的是 $\int_0^\infty e^{i t^2} dt$，它等于：

$\int_0^\infty \cos(t^2)\,dt + i \int_0^\infty \sin(t^2)\,dt = \sqrt{\frac{\pi}{8}} (1 - i)$

比较实部和虚部：

$\int_0^\infty \cos(t^2)\,dt = \sqrt{\frac{\pi}{8}}, \quad \int_0^\infty \sin(t^2)\,dt = -\sqrt{\frac{\pi}{8}} \cdot (-1) = \sqrt{\frac{\pi}{8}}$

所以：

$\boxed{\int_0^\infty \cos(t^2)\,dt = \int_0^\infty \sin(t^2)\,dt = \sqrt{\frac{\pi}{8}}}$

 参数化形式

有时也定义：

$C(a,x) = \int_0^x \cos(a t^2),dt, \quad S(a,x) = \int_0^x \sin(a t^2),dt$

当 a > 0时，可以通过变量替换 $u = \sqrt{a} t$ 得到：

$C(a,x) = \frac{1}{\sqrt{a}} C(\sqrt{a}x), \quad S(a,x) = \frac{1}{\sqrt{a}} S(\sqrt{a}x)$