物理 [TINY NSD]实数集有多少个?(四)
下面我们讨论整数的乘除法。
我们先观察自然数乘法的一条性质:
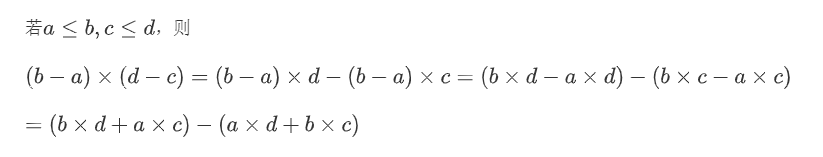
(由于${a \times d与b \times c}$无法比较大小,最后一步无法直接应用运算律,需要利用消去律进行证明,不详细解释)
按照${S_n}$的定义,若${a \leq b, 则(b, a) \in S_{b-a}}$,我们类比这种形式,可以给出整数乘法的定义:
${记S'=\lbrace (a\times c+b \times d, a \times d+b \times c) | (a, b) \in S_m, (c, d) \in S_n\rbrace}$,则${S'}$被包含于一个等价类$S'_0$,定义${S'_0 \to m \times n}$。
证明:若${(a_1, b_1), (a_2, b_2) \in S_m, (c_1, d_1), (c_2, d_2) \in S_n}$,
则${a_1+b_2=b_1+a_2, c_1+d_2=d_1+c_2}$。
只需证
${b_1 \times d_1+a_1 \times c_1+b_2 \times c_2+a_2 \times d_2=b_1\times c_1+a_1 \times d_1+b_2 \times d_2+a_2 \times c_2}$。
注意到
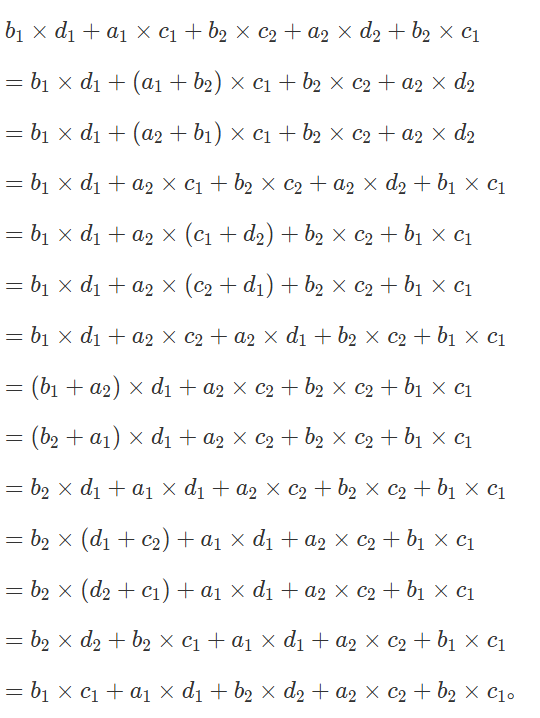








共0条回复
时间正序
回复是交流的起点,交流让学竞赛不孤单
