高数之积分 - 质心论坛

那个导数进阶帖太水了，于是被我删掉了

应大家要求，这个帖改名为高数帖，里面会有导数有关的。💦💦💦

———————————————————————————————————————

积分（Integration)是求一个函数在某个区间上的“累积效果”或“总面积”的过程。

1.1不定积分（Indefinite Integral）

定义：不定积分是求一个函数的原函数（反导数）的过程。

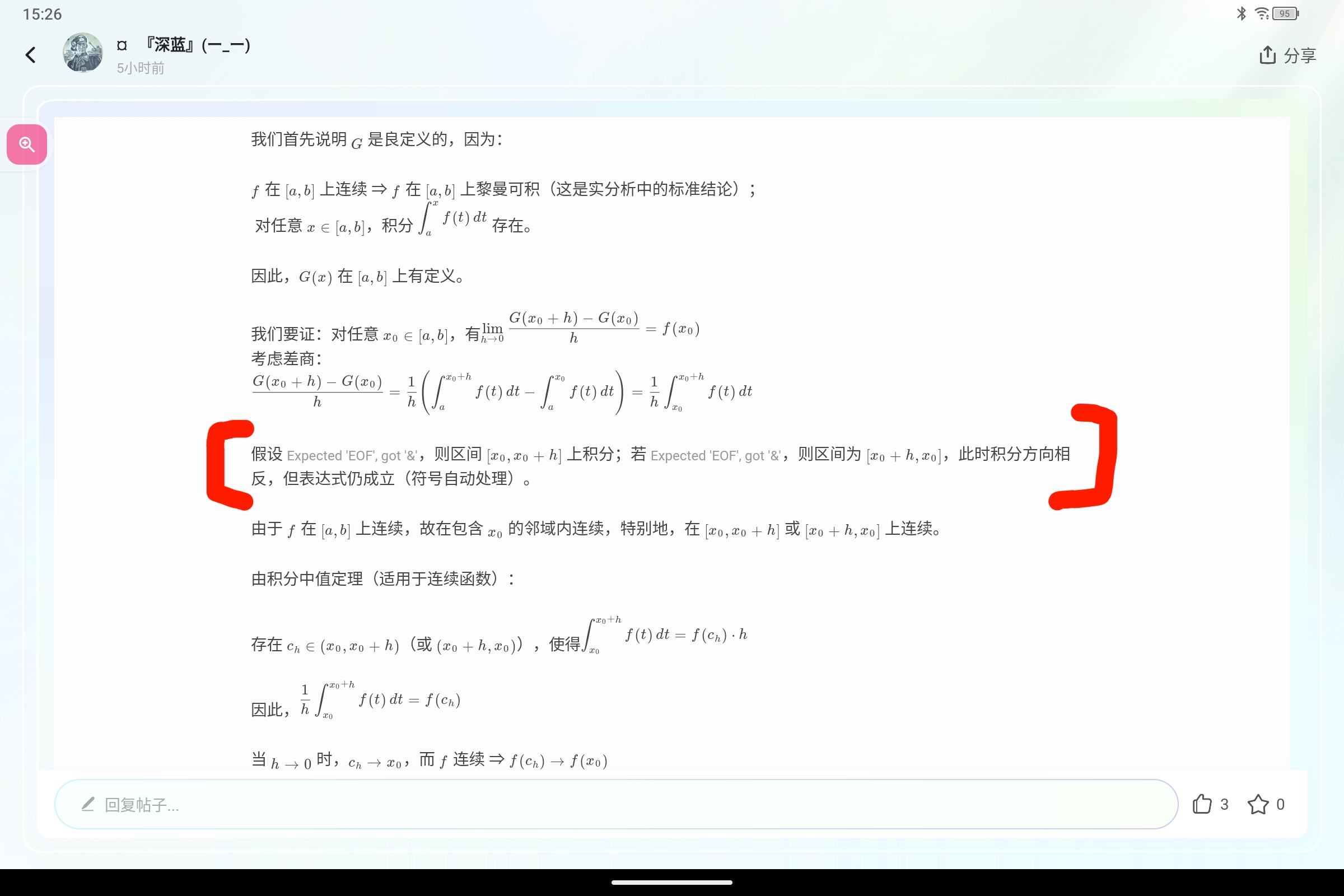
记作：$\int f(x)\,dx = F(x) + C$

其中：

$ f(x) $：被积函数

$ F(x) $：$ f(x) $ 的一个原函数，即 $ F'(x) = f(x) $

$ C $：任意常数（积分常数）

例如： $ \int 2x\,dx = x^2 + C$

因为 $ \frac{d}{dx}(x^2 + C) = 2x $

1.2常见积分公式：

| 函数 | 积分 |

| $ \int x^n\,dx $ | $ \frac{x^{n+1}}{n+1} + C $（$ n \ne -1 $） |

| $ \int \frac{1}{x}\,dx $ | $ \ln|x| + C $ |

| $ \int e^x\,dx $ | $ e^x + C $ |

| $ \int \sin x\,dx $ | $ -\cos x + C $ |

| $ \int \cos x\,dx $ | $ \sin x + C $ |

| $ \int \sec^2 x\,dx $ | $ \tan x + C $ |

2.1定积分（Definite Integral）

定义：定积分表示函数 $ f(x) $ 在区间 $[a, b]$ 上的“面积”（带符号），即：

$\int_a^b f(x)\,dx$

这个值是一个具体的实数。

几何意义：

若 $ f(x) \geq 0 $，则积分表示曲线 $ y = f(x) $ 与 $ x $ 轴在 $[a,b]$ 之间的面积。

若 $ f(x) < 0 $，面积为负，表示在 $ x $ 轴下方。

注意：定积分不包含积分常数 $ C $。

牛顿-莱布尼茨公式（微积分基本定理）：

如果 $ F(x) $ 是 $ f(x) $ 的一个原函数，则：

$\int_a^b f(x)\,dx = F(b) - F(a)$

例：

$ \int_0^1 2x\,dx = [x^2]_0^1 = 1^2 - 0^2 = 1 $

那么有的同学就要问了，如何证明牛顿/莱布尼茨公式呢？

首先，构造变上限积分函数

定义函数 $ G: [a,b] \to \mathbb{R} $ 为：

$G(x) = \int_a^x f(t)\,dt, \quad x \in [a,b]$

我们首先说明 $ G $ 是良定义的，因为：

$ f $ 在 $[a,b]$ 上连续 ⇒ $ f $ 在 $[a,b]$ 上黎曼可积（这是实分析中的标准结论）；

对任意 $ x \in [a,b] $，积分 $ \int_a^x f(t)\,dt $ 存在。

因此，$ G(x) $ 在 $[a,b]$ 上有定义。

我们要证：对任意 $ x_0 \in [a,b] $，有$\lim_{h \to 0} \frac{G(x_0 + h) - G(x_0)}{h} = f(x_0)$

考虑差商：

$\frac{G(x_0 + h) - G(x_0)}{h} = \frac{1}{h} \left( \int_a^{x_0+h} f(t)\,dt - \int_a^{x_0} f(t)\,dt \right) = \frac{1}{h} \int_{x_0}^{x_0+h} f(t)\,dt$

假设 $ h > 0 $，则区间 $[x_0, x_0+h]$ 上积分；若 $ h < 0 $，则区间为 $[x_0+h, x_0]$，此时积分方向相反，但表达式仍成立（符号自动处理）。

由于 $ f $ 在 $[a,b]$ 上连续，故在包含 $ x_0 $ 的邻域内连续，特别地，在 $[x_0, x_0+h]$ 或 $[x_0+h, x_0]$ 上连续。

由积分中值定理（适用于连续函数）：

存在 $ c_h \in (x_0, x_0+h) $（或 $ (x_0+h, x_0) $），使得$\int_{x_0}^{x_0+h} f(t)\,dt = f(c_h) \cdot h$

因此，$\frac{1}{h} \int_{x_0}^{x_0+h} f(t)\,dt = f(c_h)$

当 $ h \to 0 $ 时，$ c_h \to x_0 $，而 $ f $ 连续 ⇒ $ f(c_h) \to f(x_0) $

所以，$\lim_{h \to 0} \frac{G(x_0 + h) - G(x_0)}{h} = \lim_{h \to 0} f(c_h) = f(x_0)$

即：

$G'(x_0) = f(x_0)$

因此，$ G'(x) = f(x) $ 对所有 $ x \in [a,b] $ 成立。

我们现在知道：

- $ G'(x) = f(x) $

- $ F'(x) = f(x) $

所以，$ F'(x) = G'(x) $ 对所有 $ x \in [a,b] $ 成立。

我们需证明：存在常数 $ C $，使得 $ F(x) = G(x) + C $ 对所有 $ x \in [a,b] $ 成立。

为此，定义辅助函数：

$H(x) = F(x) - G(x), \quad x \in [a,b]$

则 $ H $ 在 $[a,b]$ 上可导，且

$H'(x) = F'(x) - G'(x) = f(x) - f(x) = 0, \quad \forall x \in [a,b]$

我们来证明：若一个函数在区间上导数恒为零，则它为常数函数。

引理：设 $ H: [a,b] \to \mathbb{R} $ 可导，且 $ H'(x) = 0 $ 对所有 $ x \in [a,b] $，则 $ H $ 为常数函数。

证明：任取 $ x_1, x_2 \in [a,b] $，不妨设 $ x_1 < x_2 $。

由于 $ H $ 在 $[x_1,x_2]$ 上连续，在 $(x_1,x_2)$ 内可导，由**拉格朗日中值定理**，存在 $ c \in (x_1,x_2) $，使得

$H(x_2) - H(x_1) = H'(c)(x_2 - x_1) = 0 \cdot (x_2 - x_1) = 0$

所以 $ H(x_1) = H(x_2) $，即 $ H $ 为常数。

因此，$ H(x) = C $，即：

$F(x) = G(x) + C, \quad \forall x \in [a,b]$

令 $ x = a $：

$F(a) = G(a) + C$

但 $ G(a) = \int_a^a f(t)\,dt = 0 $，所以：

$C = F(a)$

于是，

$F(x) = G(x) + F(a)\Rightarrow G(x) = F(x) - F(a)$

令 $ x = b $：

$G(b) = F(b) - F(a)$

但 $ G(b) = \int_a^b f(t)\,dt $，所以：

$\int_a^b f(x)\,dx = F(b) - F(a)$

依旧掀开后更

如果有不严谨的证明欢迎来喷

物理 高数之积分

物理
高数之积分