物理 初等数学(3)三角函数
还差一个反三角函数性质😋😋😋👍👍👍
1. 和差角公式
$\sin(\alpha \pm \beta) = \sin\alpha\cos\beta \pm \cos\alpha\sin\beta$;
$\cos(\alpha \pm \beta) = \cos\alpha\cos\beta \mp \sin\alpha\sin\beta$;
$\tan(\alpha \pm \beta) = \dfrac{\tan\alpha \pm \tan\beta}{1 \mp \tan\alpha \cdot \tan\beta}$;
$\cot(\alpha \pm \beta) = \dfrac{\cot\alpha \cdot \cot\beta \mp 1}{\cot\beta \pm \cot\alpha}$。
2. 和差化积公式
$\sin\alpha + \sin\beta = 2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}$;
$\sin\alpha - \sin\beta = 2\cos\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2}$;
$\cos\alpha + \cos\beta = 2\cos\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}$;
$\cos\alpha - \cos\beta = -2\sin\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2}$。
3. 倍角公式
$\sin 2\alpha = 2\sin\alpha\cos\alpha$;
$\cos 2\alpha = 2\cos^2\alpha - 1 = 1 - 2\sin^2\alpha = \cos^2\alpha - \sin^2\alpha$。
4. 半角公式
$\sin\dfrac{\alpha}{2} = \pm\sqrt{\dfrac{1 - \cos\alpha}{2}}$;
$\cos\dfrac{\alpha}{2} = \pm\sqrt{\dfrac{1 + \cos\alpha}{2}}$;
$\tan\dfrac{\alpha}{2} = \pm\sqrt{\dfrac{1 - \cos\alpha}{1 + \cos\alpha}} = \dfrac{\sin\alpha}{1 + \cos\alpha} = \dfrac{1 - \cos\alpha}{\sin\alpha}$;
$\cot\dfrac{\alpha}{2} = \pm\sqrt{\dfrac{1 + \cos\alpha}{1 - \cos\alpha}} = \dfrac{1 + \cos\alpha}{\sin\alpha} = \dfrac{\sin\alpha}{1 - \cos\alpha}$。
5. 正弦定理
$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R$。
6. 余弦定理
$c^2 = a^2 + b^2 - 2ab\cos C$。

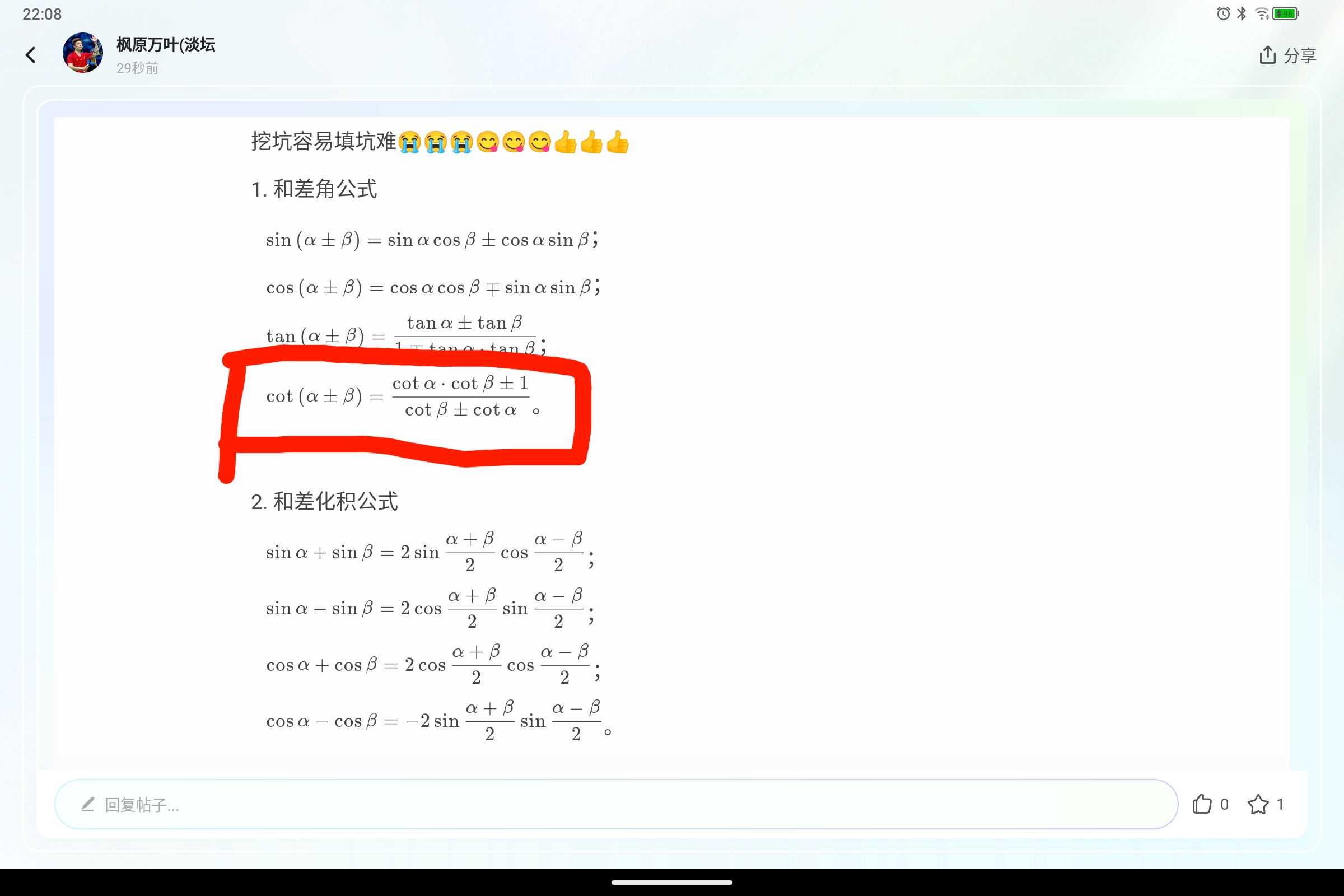 这里分母上的符号是不是反了?
这里分母上的符号是不是反了?