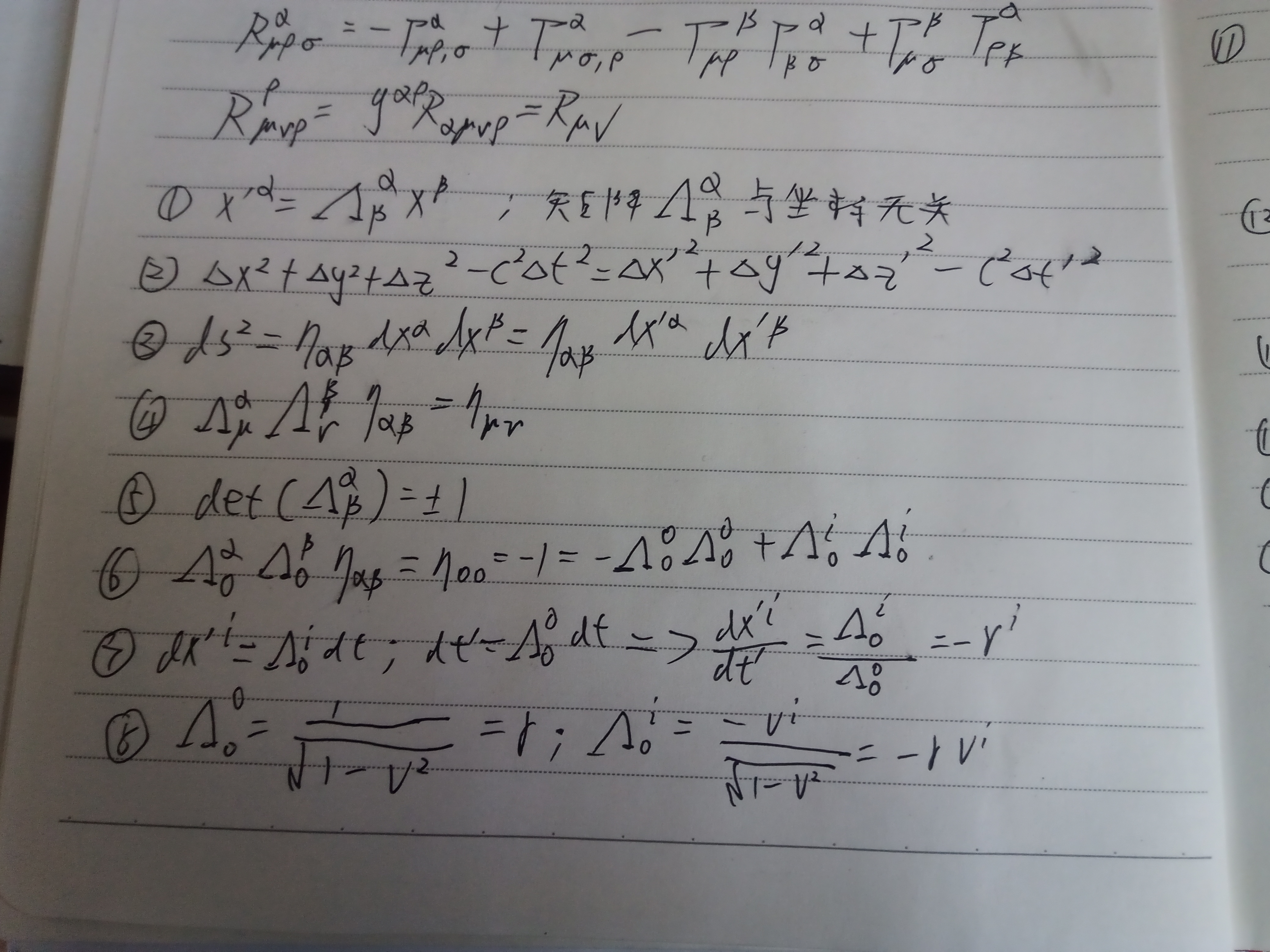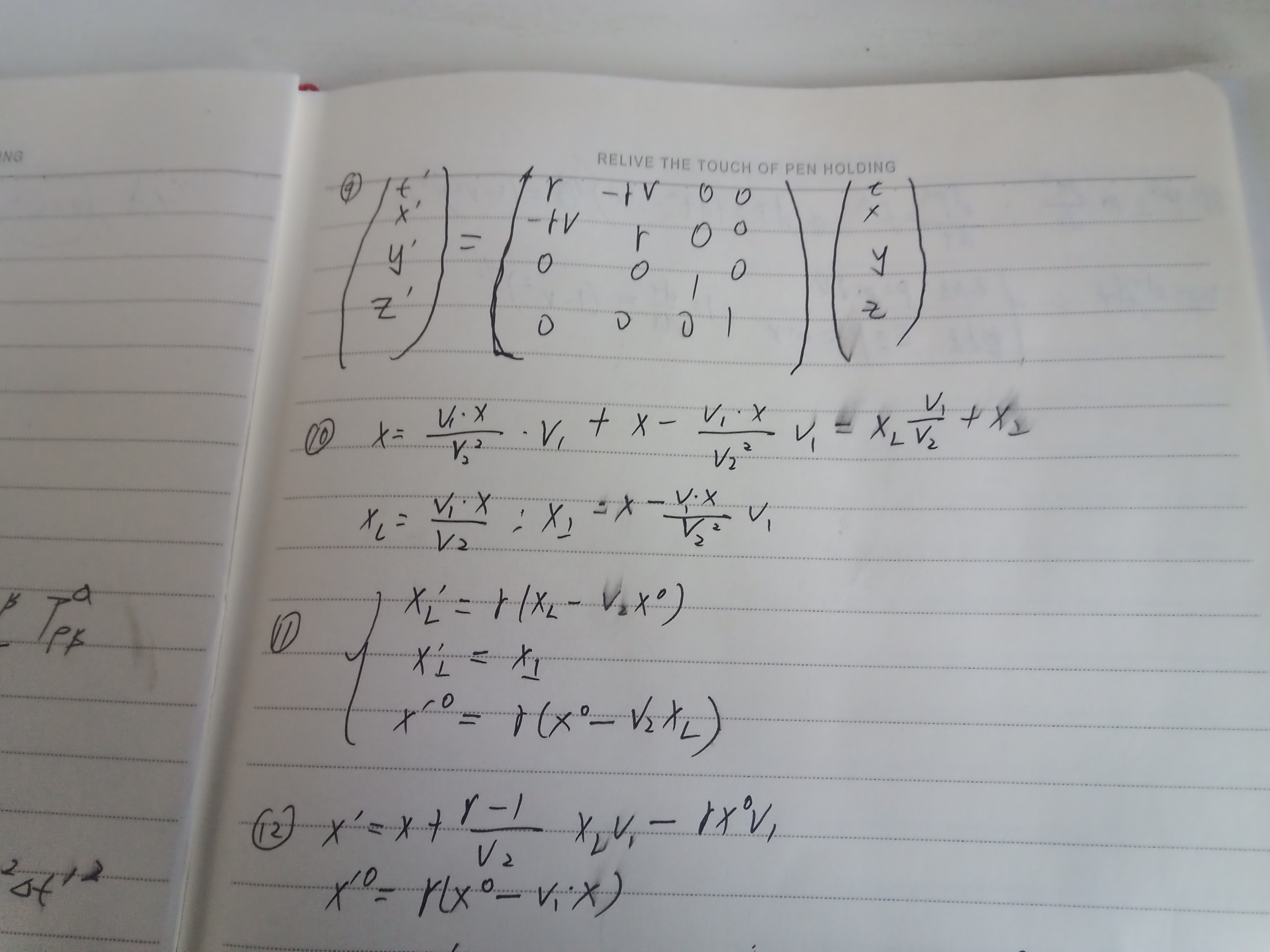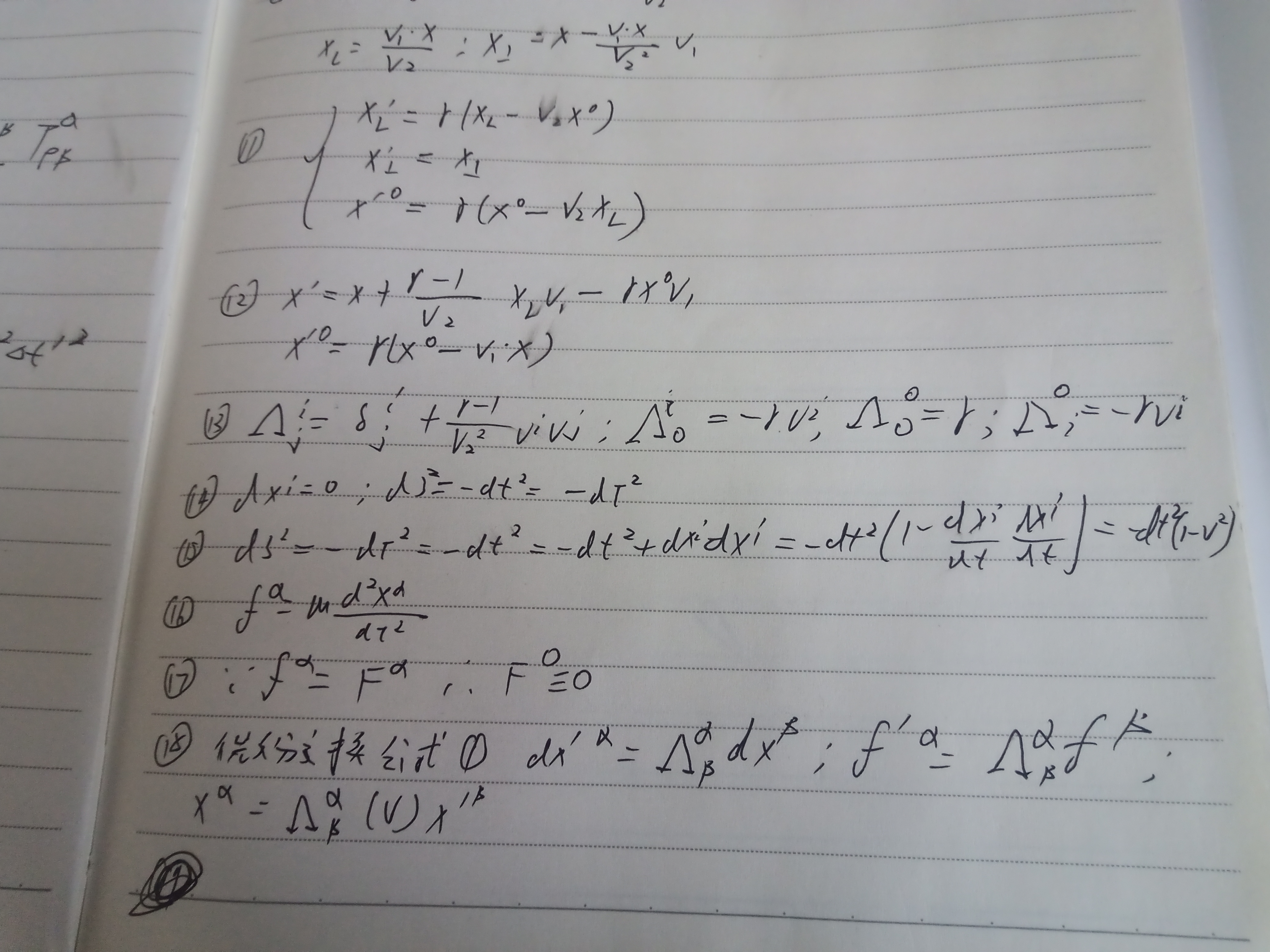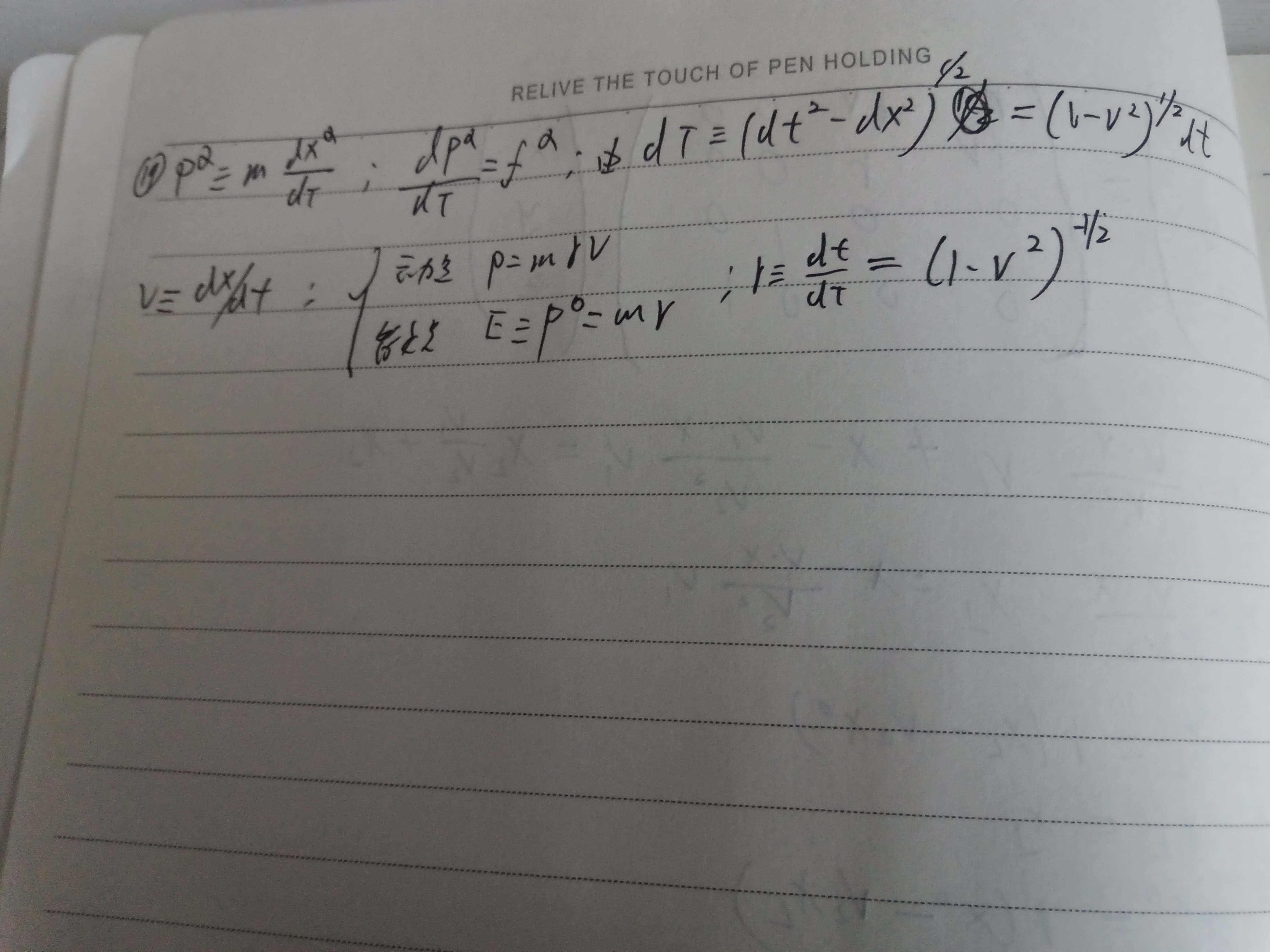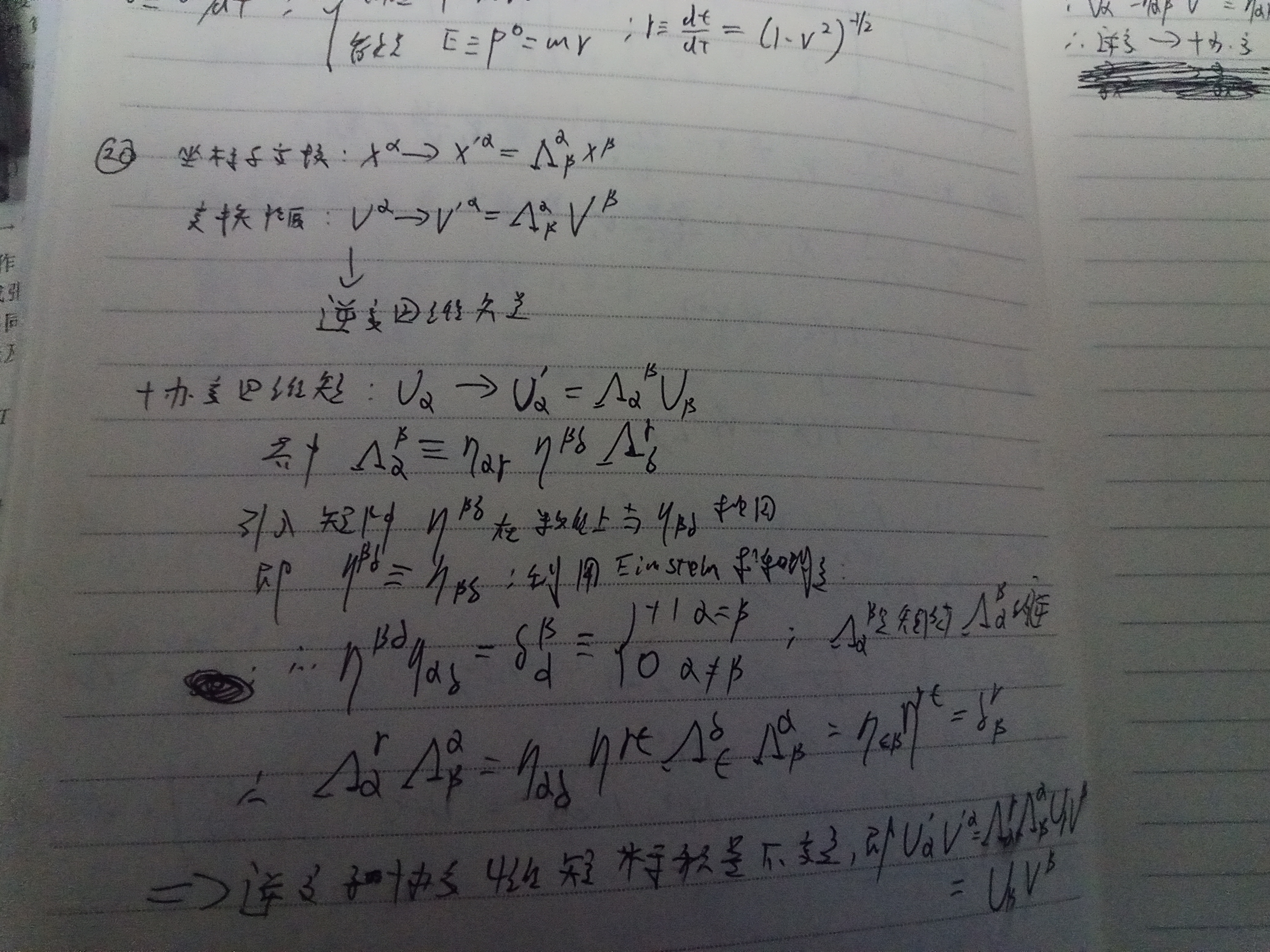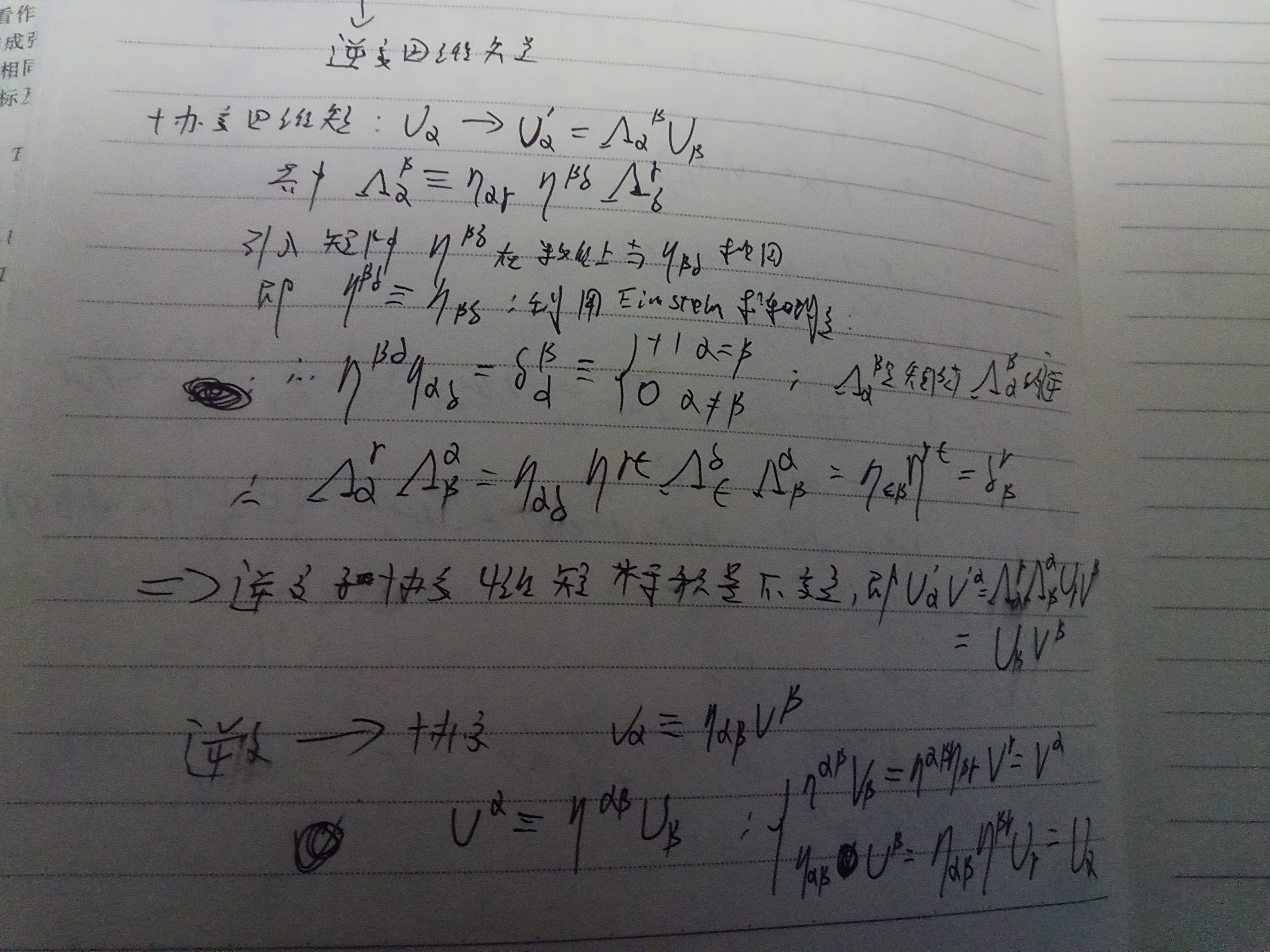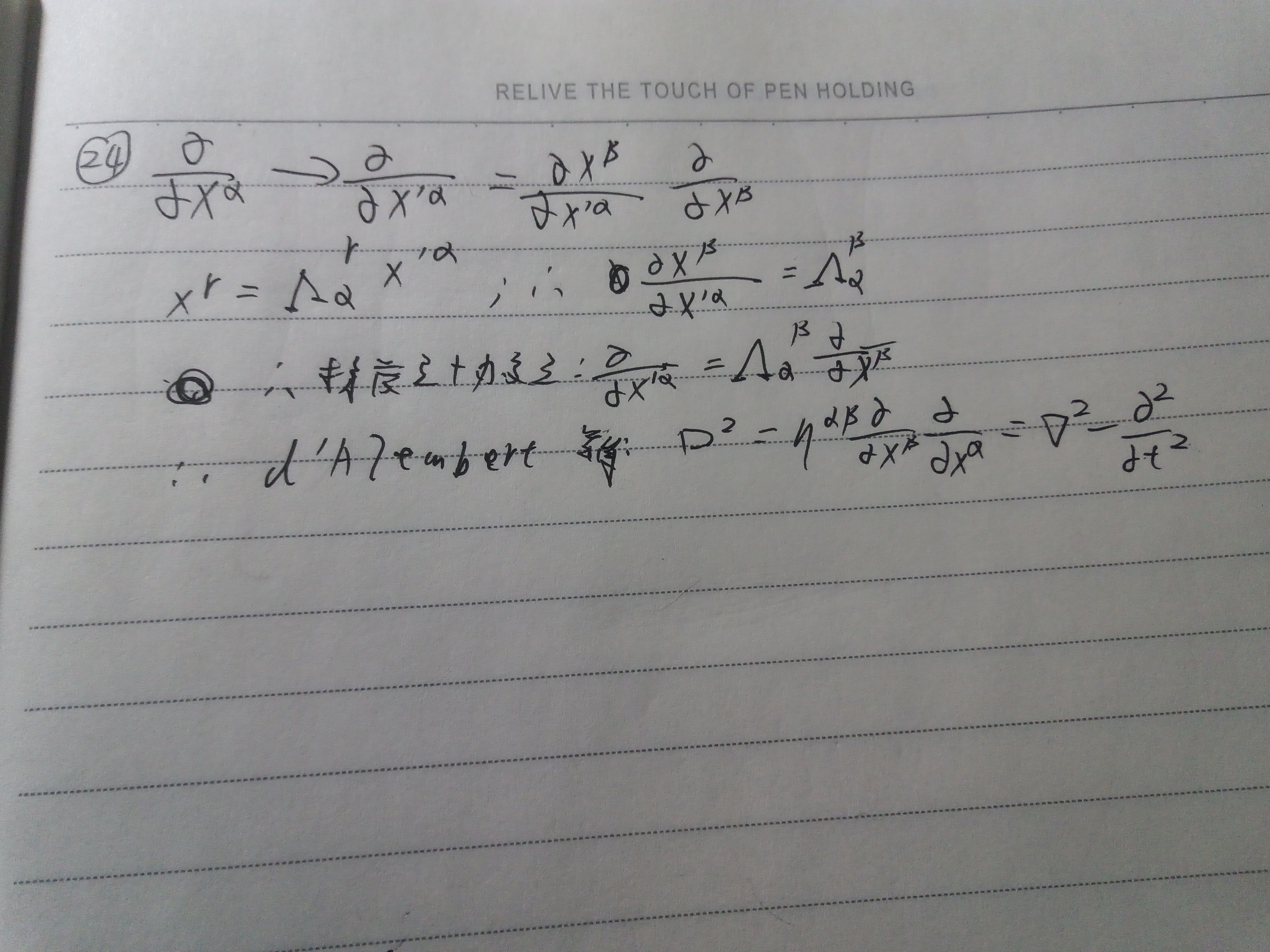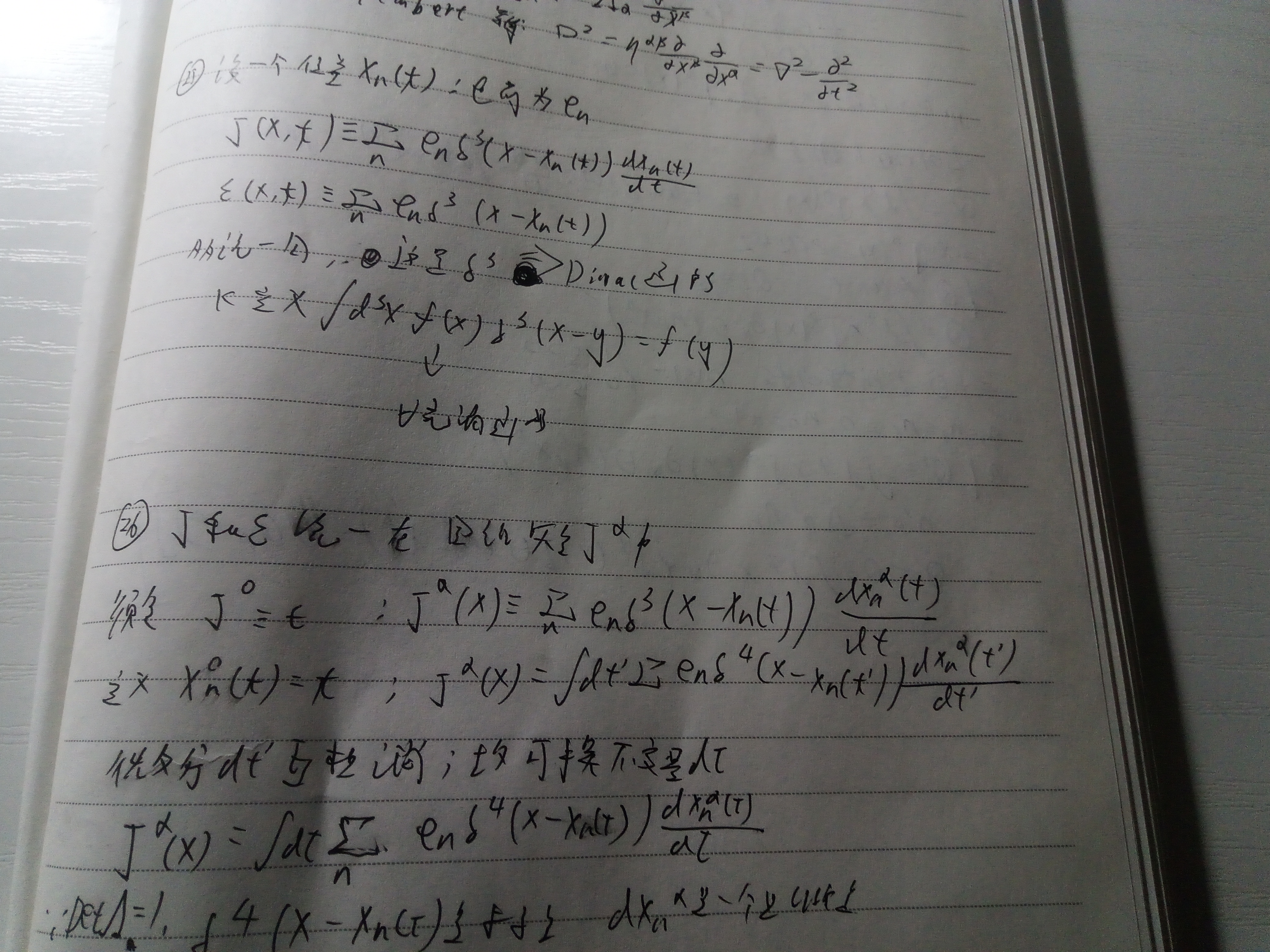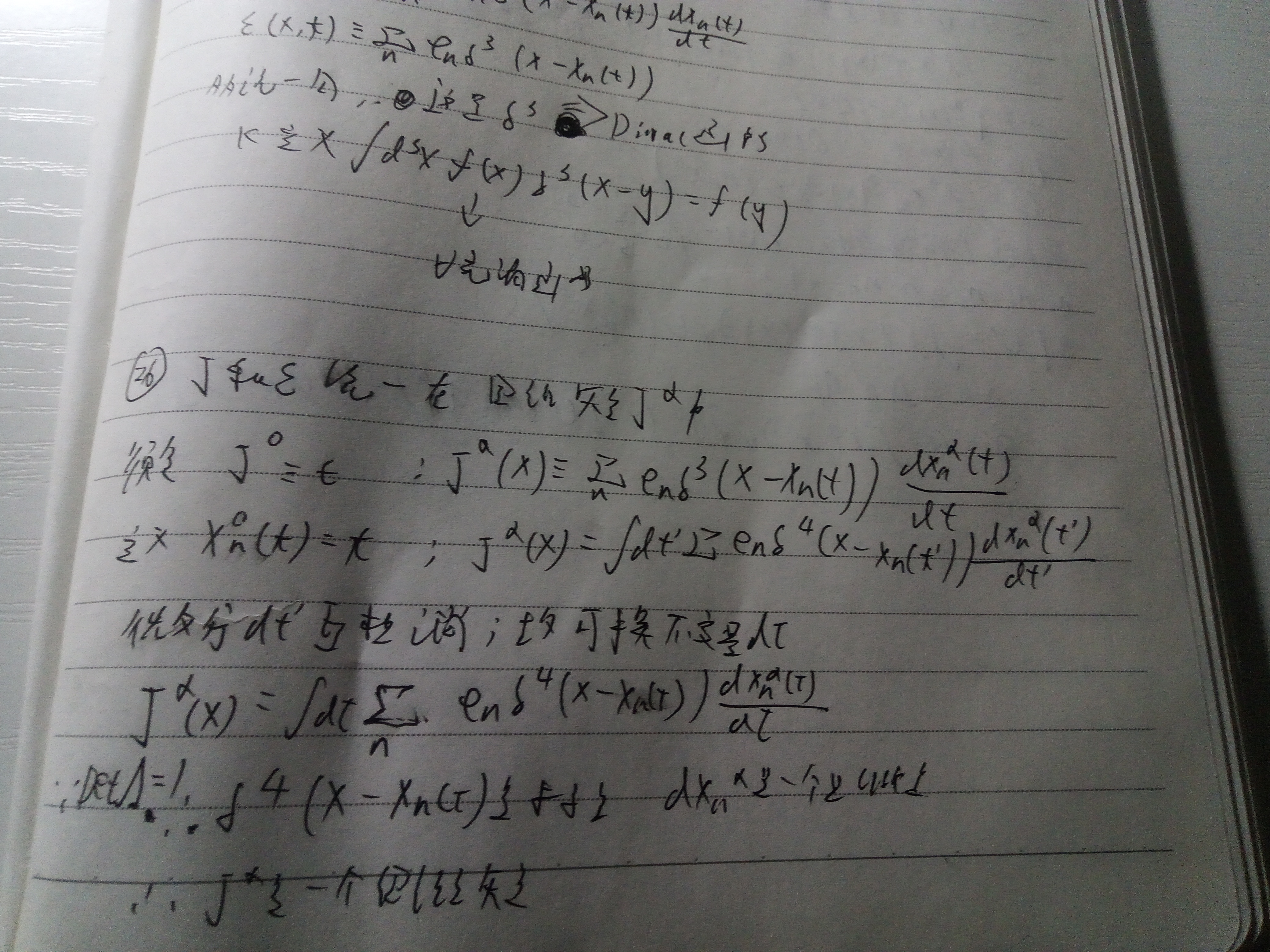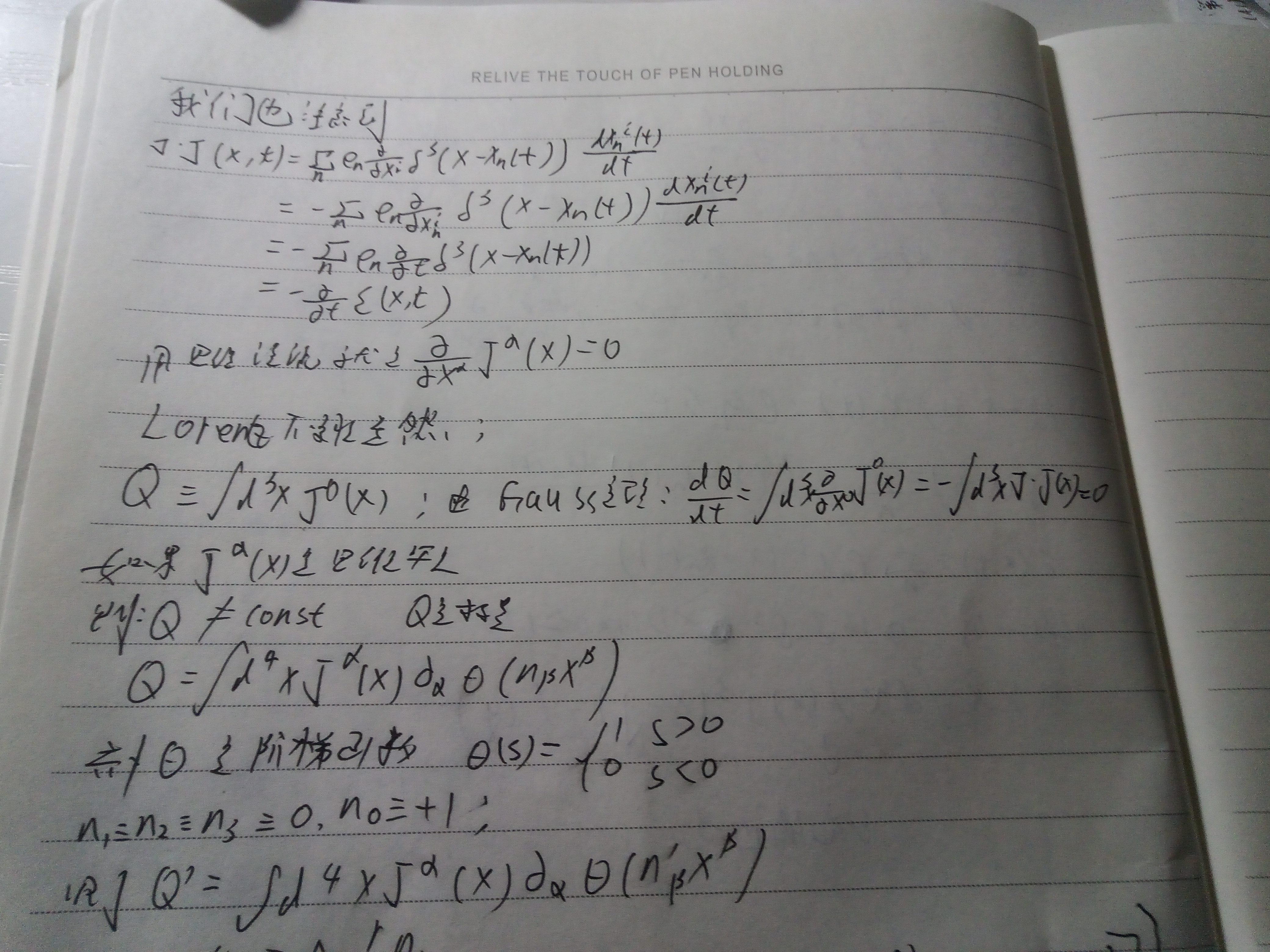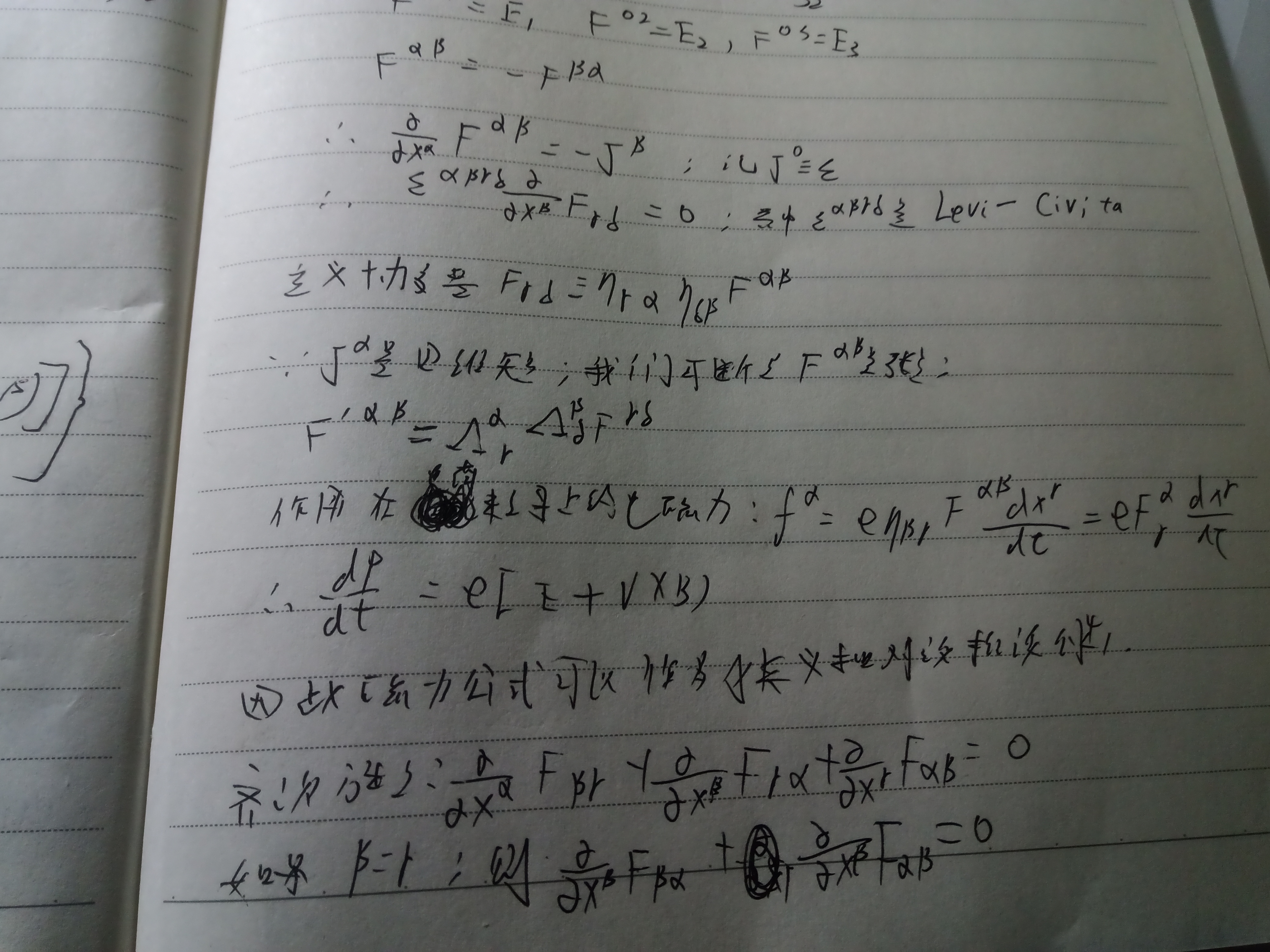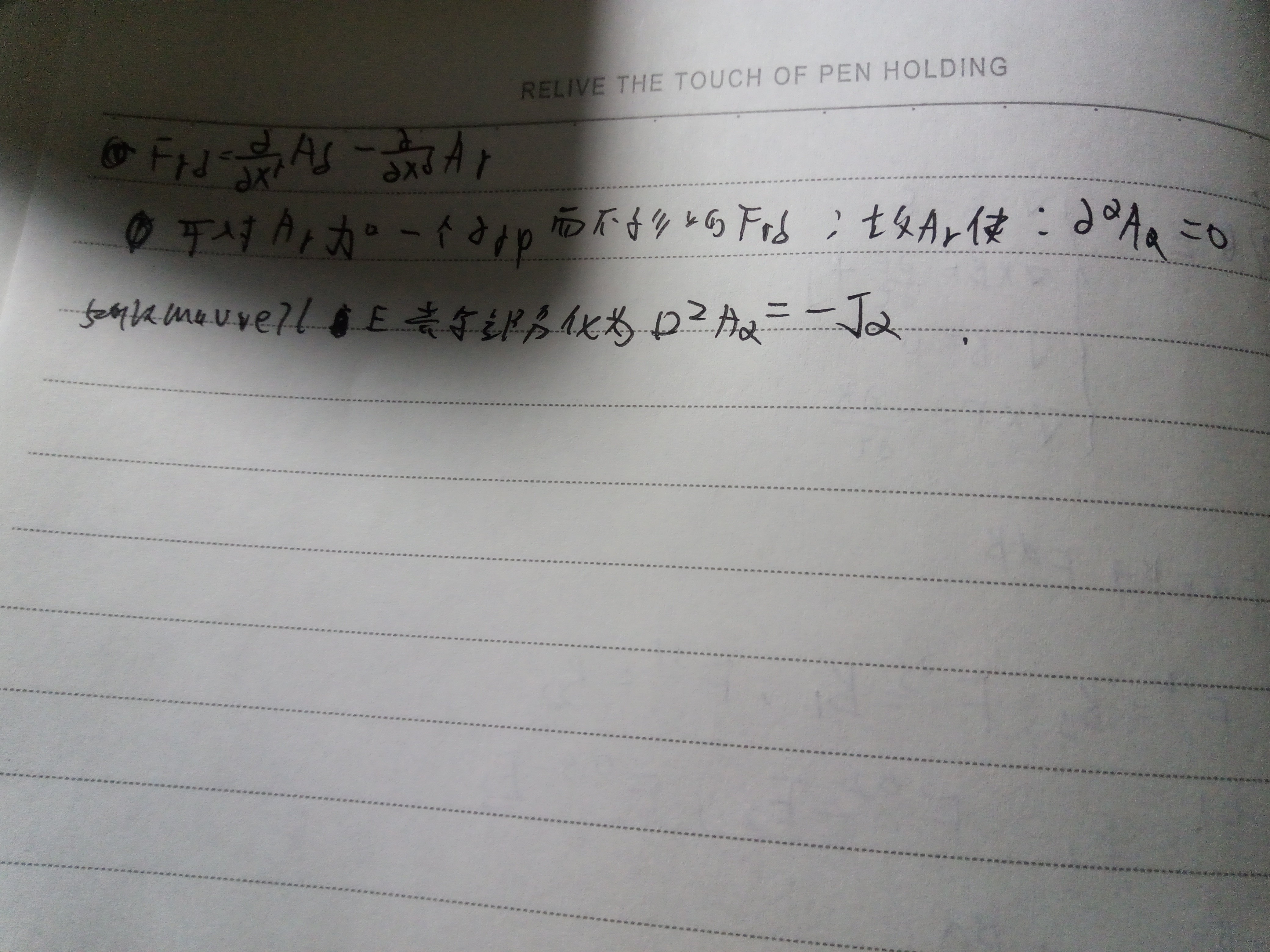物理 广义相对论
因为某某原因，所以打算开一个广义相对论的帖，至于这个帖，可能帖主是个弱弱的高中生，所以讲的不是这么好，目标：5天更完，感觉不太可能，之后的内容会在评论区讲为了避免内容太多导致帖子非常卡，就说一句，欢迎错误指正
为了让更多听懂，所以我打算先讲一讲狭义相对论，首先我们先约定一下，我在每次帖子的最后面都会发一张图片，就假设洛伦兹变换为公式圆圈一，我会在图片写好，还有，约定所以人都会张量分析，我这里因为是给广义相对论做铺垫肯定是张量分析表达，至于数学内容因为省时省，其实数学内容不难主要计算，所以考虑简洁性，所以不讲了
第一章狭义相对论，1.1洛伦兹变换
约定：光速不变原理，伽利略变换被修正成洛伦兹变换，即公式1，且洛伦兹变换是关于坐标的线性变换
然后定义距离，且在任何参照系下不变，即自然定律对洛伦兹变换群是不变的，即公式2，然后约定c=1吧，公式二可以写成公式三，这里考虑到了度规负号，好吧，那我在约定第0公式是一些前置约定，可能我想什么就写什么，所以第0公式会比较多，另外说一下，公式3用了爱因斯坦求和阅读
然后距离不依赖坐标的选取，即出现一个闵可夫斯基空间，就叫四维时空，在这里我们定义一个名称叫事件，就是某时刻在某地的事情，代表一个时空点
有ds^2<0，叫类时.ds^2=0，叫类光.ds^2>0，叫类空.
类时表明两个事件有因果关系，在任何参照系中，两个事件的时间顺序一样，且存在一个参照系两个事件在相同空间位置；
类空表明两个事件没有因果关系，在不同参照系中，两个事件的时间顺序可以不同，且存在一个参照系两个事件同时发生；
类光是临界事件，两个事件要么在任何参照系里都同时发生，要么都不同时且不同地
公式1可以被看成四维时空的旋转，因为要保证所有坐标系距离不变，旋转矩阵满足条件公式四，由公式四可知公式五
考虑公式四中的时间分量，有公式六，一般情况下，带有时间指标0的矩阵元可以通过考察两个以v速度相对运动的观测者的观测结果得
在S系中的静止物体，在S'系看来速度是-v，所以由公式一可得公式七，代入公式六，得公式8，甚于的矩阵元和单纯空间旋转有关.
写一个洛伦兹变换矩阵形式，即公式九，这个公式可以推广到任意相对速度的洛伦兹变换，三维坐标相对速度方向纵向投影分量和横向，即公式十
然后因为公式九又可推公式11，合并里面分量得公式十二，所以自然可有公式十三.
不过由于狭义相对论本人想让更多人听懂，所以决定公式以及公式的数学意义中不加入群论的知识条件了
1.2固有时，时间膨胀和尺缩
这里再说明一件事，坐标系和参照系在狭义相对论中没有太大区别，占时先属于一个概念
另外在狭义相对论中，两个事件的时间和间隔在不同参考系，所以在类时中，存在一个坐标系，两个事件在同一空间位置发生，只是时间会有差值，叫固有时，即公式十四.
固有时的微元的平方与四维距离平方差一个负号，所以固有时也是洛伦兹不变量，它代表的是类时世界线的四维长度，所以在任意坐标系中，两个类时事件的时间间隔和固有时的关系为公式15，两个类时事件的时间间隔以固有时为最短，所以叫时间膨胀.
2.3粒子动力学
我们假定粒子的运动像在电动力学一样，我们定义一个作用于坐标为x上指标a的粒子上的相对论性的力，见公式十六，相对论性力有以下两个性质：
1.如果粒子是瞬时静止的，有固有时间隔等于dt，所以可以和牛顿力联系起来，即公式十七
2.在一般洛伦兹变换下坐标微分的变换规则是公式一的微分，由于固有时是不变量，固公式十六告诉我们，相对论性力具有洛伦兹变换的规则，即公式18
2.4能量和动量
接下来就是继续把动量和能量的那些公式在相对论情况下重新定义，即公式19，有比较多的公式
好像还有一些东西没讲，就是由其他张量构成张量
(A)线性组合：具有相同上标及下标的一些张量线性组合后仍是一个张量，且有与之相同的上标及下标
（B）直积：两张量分量的乘积产生一个张量，其上标和下标由原二张量的上标下标构成
（C）缩并：令一个上标及一个下标相同，再将他们赋0，1，2，3求和，则产生一个只缺少此二指标的张量
（D）微商：任何张量的导数是增加一个下标的张量
另外存在三种张量其分量在所有坐标系中相等
1.Minkowski张量在洛伦兹变换下的定义直接告诉我们看公式21，会有略微详细的推导
2.Levi-Civita张量怎么定义，见公式22
3.零张量:我们可以定义一个具有任意选取的上指标下指标式样的张量为0张量，只需另其全部分量是0即可。多补充一个代数要点：它使我们能一眼看出是否是Lorentz不变的，基本定理是：两个具有相同的上标及下标的张量在一个坐标系中相等，则可以通过Lorentz变换与相连系的任何其他坐标系中也相等。详细推导见公式23
多加一个推导d'Alembert算符详情见公式24
我现在准备讲一讲电动力学，不过内容会非常少，主要就是稍微拓展延伸一下，嗯对
2.5电流与密度，大概说一下这个2.55类似的东西我会在讲很多了以后在同一整理一下，至于这个不能算电动力学只能说是打铺垫
开始我们先假设一个粒子系统有位置和电荷，电流密度和电荷密度定义见公式25即可
说两个技巧吧，不是代数技巧，代数技巧相信自己就可以观看
1.每当任意一个电流满足不变的守恒定律时，我们可以构造一个总电荷
2.在处理有广延的粒子电荷分布与电流分布时对任何守恒的四维矢量定义与时间无关的标量～～然后请看图片
开始讲电动力学，额额，发现现在讲了总进度可能大概预估一下五分之一都不到，好吧
2.6电动力学
可能又是全部推导，四大就是这样，好吧，主要起点就是Maxwell方程看图片，这次一大坨公式就叫27吧
- 1
开始讲电动力学的能动量
2.7电动力学的能动量
似乎又是一大堆推导，等等，感觉还稍稍需要构造，太好了，边构造边推导，可以，看图，就叫公式28
算了，说句话吧，我们需要对能动量四维矢量的密度和流密度给出定义，可能当时搞这个人就是靠着刚刚电动力学那里的形式大概猜出来的
首先考虑一组由n标记的粒子～～应该只能说这么点话了
2.8张量分析
先说明一下，在广义相对论里经常会出现仿射，意思就是线性，首先有向量空间V，在物理大概率n＝1，2，3，4，有对偶空间V*,可以这么说物理上大部分的东西全部是线性结构的，所以这个张量代数也不例外满足线性空间的所有性质
即V上所有线性泛函，线性映射f：V→R构成的
继续2.8张量代数
基底那些因为有数学内容我不会打所以选择发图，继续讲一讲爱因斯坦求和约定
规则:一个指标字母如果在上标和下标各出现一次，则自动代表对该指标所有维度求和，给了几个例子在图片里
其他的我好像刚刚讲过了，待会看看是哪里
2.9张量分析
2.9.1广义协变原理
等效原理表明可以估计计算引力对物理系统的影响简单的方法：对一般的引力场，我们写局部惯性系里成立的方程，然后进行一个坐标变换，找在实验室坐标系里的相应方程我们要得到的是完整的引力场和电磁场的方程，所以需要引入广义协变性原理，主要是简便物理计算
物理方程在一般的引力场中也成立，只需要具备两个条件
（1）当度规张量等于Minkowski张量，而且仿射联络为零时，它和狭义相对论定律一致
（2）这个方程是广义协变的，即在一般坐标变换x→x'时它保持自己的形式不变
还要说一下广义协变原理来自等效原理，就这么解释吧，假设我们处在任意的引力场中，考虑任何满足条件的方程，由条件（2）我们知道，这个方程只要在任意坐标系中成立，就将在所有坐标系都成立，然而任意的给定点，存在一类坐标系，即局部惯性系，但是引力效应不存在
于是条件（1）告诉我们方程在这一类坐标系中成立，因此在其他坐标系中也成立，另外，因为这里涉及到了广义相对论的原因，所以这里的坐标系不再等于参考系，这里再多提醒一句，本来是打算后面讲的，不过因为原因，所以打算先讲
不过不要以为广义协变和广义相对论扯上关系就有物理意义，其实它本身没有物理内涵，任意方程都可以被广义协变好吧，只要在任意一个坐标系中写下他然后算他在其他坐标系中的形态即可
就结束了
2.9.2矢量和张量
我们需要构造一般坐标下不变的物理方程，我们必须知道方程元素的物理意义
所有变换规则中最简单的就是标量变换，标量在一般坐标下不变
具体说一下张量中对矢量定义，就是只有一个指标的张量，而标量指标为0，不过多说一句仿射联络看起来是张量，其实不是
存在一大类不变的方程，任何方程只要它是两个同样上下指标张量的等式，在一般坐标变换下都是不变的，就说这么多
然后看图片公式30
2.9.3张量密度
因为我记得前面讲过张量代数了，可以往前面的聊天翻翻，现在大概讲一下张量密度在广义相对论中需要的内容
说一句，张量的变换规律并不是不能违反的，比如一个非张量但是是度规张量的行列式，详情看公式31
度规张量的变换规则可以看成一个矩阵方程，详情见公式32，取公式32的行列式，可得公式33，特别说一句，公式33中类似于g这种量，它的变换比标量变换多出几个Jacobi行列式因子，称为标量密度，详细内容看图片
再介绍一个Levi-Civita张量密度，看公式34
总结：张量代数的法则可以推广到包含张量密度的情形
（A）权同为W的两个张量密度的线性组合仍然是权为W的张量密度
（B）权为W_1,W_2的两个张量密度的直积构成一个权为W_1+W_2的张量密度
（C)权为W的张量密度指标缩并后得到权为W的张量密度，由（B）（C）可以推出得，指标的升降并不改变张量密度的权
佬，你为啥没去上学啊？（纯好奇）
我自学啊，怎么啦
佬几年级啊？
高二！
膜拜😋
2.9.4仿射联络的变换
仿射联络记得是非张量，而且在物理学中广泛使用
由于这里大多都是计算推导内容，所以我只说一句话方程在任意一个坐标系成立则在所有坐标系都成立，在局部惯性坐标系里方程也是正确的
详情请看公式35
