物理

【广义相对论速成版】3. 中心球对称解与新引力效应 3.7 黑洞

质量超过临界质量

$$M_{\max }=3.2 \mathrm{M}_{\odot}$$

的致密星冷却后将塌缩成半径为

$$R<r_{S}=\frac{2 G M}{c^{2}}$$

的黑洞。

1. $r=\frac{2GM}{c^{2}}$的界面称为视界(Schwarzschild Horizon)

设光由$P_{1}$点传播到$P_{2}$点，在$P_{1}$点光的频率为$\mu_{1}$，传至$P_{2}$点，观测到的频率为$\mu_{2}$，则

$$\frac{\nu_{2}}{\nu_{1}}=\frac{\sqrt{-\left(g_{00}\right)_{1}}}{\sqrt{-\left(g_{00}\right)_{2}}}$$

若恒星的质量为$M$，则距星心$r$处

$$-g_{00}=1-\frac{2 G M}{c^{2}}=1-\frac{r_{S}}{r}, r_{S}=\frac{2 G M}{c^{2}}$$

当$M>3.2M_{\odot}$，恒星塌缩后，可有

$$R<r_{S}$$

(见图如下)

令$P_{2}$点$r\gg r_{S}$，$P_{1}$点$r$接近$r_{S}$，则

$$-\left(g_{00}\right)_{1}=1-\frac{r_{S}}{r_{1}}$$

$$-\left(g_{00}\right)_{1}=1-\frac{r_{S}}{r_{1}}$$

故

$$\frac{\nu_{2}}{\nu_{1}}=\sqrt{1-\frac{r_{S}}{r_{1}}}$$

即

$$\nu_{\infty}=\nu \sqrt{1-\frac{r_{S}}{r_{1}}}, \quad \nu_{\infty}=\nu_{2}, \quad \nu=\nu_{1}$$

故若星体塌缩为黑洞，由$r=r_{S}$处发出的频率为$\nu$的光波在远离黑洞处观测到的频率

$$\nu_{\infty}=0$$

即观测到的频率为零，也即观测不到界面$r=r_{S}$处发出的光波 

$$\text{半径为$r_{S}$的球面称为视界}$$

视界内黑洞发的光在视界外永远观察不到，这是黑洞名称的来源。

黑洞的定义指视界内区域。以$r_{S}=\frac{2GM}{c^{2}}$为界面的黑洞称为Schwarzschild黑洞。

下面进一步研究光由视界面传至远方的时间

$$\mathrm{d} s^{2}=\left(1-\frac{2 G M}{c^{2} r}\right) c^{2} \mathrm{d} t^{2}-\frac{\mathrm{d} r^{2}}{1-\frac{2 G M}{c^{2} \tau}}=0$$

故

$$\mathrm{d} t^{2}=\frac{1}{c^{2}} \frac{\mathrm{d} r^{2}}{\left(1-\frac{2 G M}{c^{2} r}\right)^{2}}=\frac{1}{c^{2}} \frac{\mathrm{d} r^{2}}{\left(1-\frac{r s}{r}\right)^{2}}$$

则

$$\mathrm{d} t=\frac{1}{c} \frac{\mathrm{d} r}{\left(1-\frac{r_{S}}{r}\right)}$$

即

$$\mathrm{d}  t=\frac{1}{c}\left[1+\frac{r_{S}}{r-r_{S}}\right] \mathrm{d} r$$

设光出发点为$r_{1}$，观测点为$r_{2}$，则由$r_{1}$传至$r_{2}$的时间

$$\Delta t=t_{2}-t_{1}=\frac{1}{c} \int_{r_{1}}^{r_{2}}\left[1+\frac{r_{S}}{r-r_{S}}\right] \mathrm{d} r=\frac{1}{c}\left.\left[r+r_{S} \ln\left(r-r_{S}\right)\right]\right|_{r_{1}} ^{r_{2}}$$

即

$$\Delta t=\frac{1}{c}\left\{\left(r_{2}-r_{1}\right)+r_{S}\left[\ln \left(r_{2}-r_{S}\right)-\ln \left(r_{1}-r_{S}\right)\right]\right\}$$

若光由黑洞视界面上发出，即$r=r_{S}$，则

$$\Delta t=+\infty, \quad(\ln 0=-\infty)$$

即光由黑洞视界面发出，传播至观测处，时间为无穷大。也即在黑洞视界以外永远观测不到黑洞视界面或视界内发出的光。

2. 粒子向黑洞中心的运动的固有时

对Schwarzschild度规，$x^{0}$分量的短程线方程可导得

$$e^{\nu}\left(\frac{\mathrm{d} t}{\mathrm{d} s}\right)=k, \quad e^{\nu}=1-\frac{2 G M}{c^{2} r},\quad k\text{为积分常数}$$

$$\mathrm{d} s=c \mathrm{d} \tau, \quad \tau\text{称为固有时，与不变弧元有关}$$

$r$方向运动，$\theta$和$\phi$不变，弧元

$$\frac{\mathrm{d} t}{\mathrm{d} \tau}=\frac{k c}{1-\frac{2 G M}{c^{2} r}}$$

利用$\mathrm{d}s=c\mathrm{d}r$，可得

$$\mathrm{d} s^{2}=\left(1-\frac{2 G M}{c^{2} r}\right) c^{2} \mathrm{d} t^{2}-\frac{1}{1-\frac{2 G M}{c^{2} r}} \mathrm{d} r^{2}$$

将$\frac{\mathrm{d}t}{\mathrm{d}\tau}$公式代入可得

$$\left(\frac{\mathrm{d} r}{\mathrm{d} \tau}\right)^{2}=\left[(k c)^{2}-\left(1-\frac{2 G M}{c^{2} r}\right)\right] c^{2}$$

设粒子由$r=r_{1}$点向黑洞沿径向$r$方向飞，且$\frac{\mathrm{d}r}{\mathrm{d}\tau}=0$(初速为零)，则由上式可知

$$(k c)^{2}=1-\frac{2 G M}{c^{2} r_{1}}$$

将$kc$代入$\frac{\mathrm{d}r}{\mathrm{d}\tau}$公式可得

$$\left(\frac{\mathrm{d} r}{\mathrm{d} \tau}\right)^{2}=2 G M\left(\frac{1}{r}-\frac{1}{r_{1}}\right)$$

此方程具有下列参数解

$$\begin{aligned}r &=\frac{1}{2} r_{2}(1+\cos \alpha) \\ \tau &=\frac{1}{2} r_{1} \sqrt{\frac{r_{1}}{2 G M}}(\alpha+\sin \alpha),\quad\alpha\text{为参数}\end{aligned}$$

由上式可知当$\alpha=0$时，$\tau=0,r=r_{1}$，此后$\tau$随着$\alpha$的增加而增加，$r$随着$\alpha$的增加而减小，这是向中心运动的特征。

当$r=\frac{2GM}{c^{2}}=r_{S}$，即粒子到达视界面时

$$\frac{2 G M}{c^{2}}=\frac{1}{2} r_{1}(1+\cos \alpha)$$

得

$$\cos \alpha=1-\frac{4 G M}{c^{2} r_{1}}$$

即$\alpha$略大于零($\alpha$是有限值)。故粒子由$r=r_{1}$到达视界面$r=r_{S}$的时间是有限的。

当$\alpha=\pi$时，$r=0$，故由$r_{1}$到达黑洞$r_{S}$的时间

$$\tau=\frac{1}{2} r_{1} \sqrt{\frac{r_{1}}{2 G M}} \pi$$

时间是有限的。当$r_{1}=r_{S}=\frac{2GM}{c^{2}}$，可得

$$\tau=\frac{r_{S} \pi}{2 c}$$

上式决定粒子由视界面落入中心的时间。

黑洞：

$$M=\eta M_{\odot}, \quad \eta>3.2$$

对太阳：

$$\frac{2 G M}{c^{2}}=2.9532 \mathrm{k m}$$

对黑洞：

$$r_{S}=\eta \times 2.9532 \mathrm{km}, \quad c=2.998 \times 10^{5} \mathrm{km/sec}$$

则可算得

$$\tau=\frac{\pi}{2 c} \times \eta \times 2.9532 \mathrm{km}=1.547 \times \eta \times 10^{-5} \mathrm{sec}$$

$$\tau \sim\text{几十微秒}$$

此外由

$$\left(\frac{\mathrm{d} r}{\mathrm{d} \tau}\right)^{2}=2 G M\left(\frac{1}{r}-\frac{1}{r_{1}}\right), \quad r \leqslant r_{1}$$

可知

$$\frac{\mathrm{d} r}{\mathrm{d} \tau}=-\sqrt{2 G M} \sqrt{\left(\frac{1}{r}-\frac{1}{r_{1}}\right)}$$

看出，当

$$r=r_{1} \longrightarrow r_{S}$$

$\frac{\mathrm{d}r}{\mathrm{d}\tau}$是有限的。由于$r_{S}\ll r_{1}$，则

$$\left(\frac{\mathrm{d} r}{\mathrm{d} \tau}\right)_{r \simeq r_{S}}=-\sqrt{2 G M} \sqrt{\frac{1}{r_{S}}}=-\sqrt{\frac{2 G M}{r_{S}}}=-c$$

即粒子是以比光速小一些的速度穿过视界的。

3. 坐标时$t$的表述

由上节公式，令

$$r_{S}=\frac{2 G M}{c^{2}}$$

可有

$$\left(\frac{\mathrm{d} t}{\mathrm{d} \tau}\right)^{2}=\frac{(k c)^{2}}{\left(1-\frac{r s}{r}\right)^{2}}$$

和

$$(k c)^{2}=1-\frac{r_{S}}{r_{1}}$$

可得

$$\left(\frac{\mathrm{d} \tau}{\mathrm{d} t}\right)^{2}=\frac{\left(1-\frac{r_{S}}{r}\right)^{2}}{1-\frac{r_{S}}{r_{1}}}$$

此外，由上节可知

$$\left(\frac{\mathrm{d} r}{\mathrm{d} \tau}\right)^{2}=2 G M\left(\frac{1}{r}-\frac{1}{r_{1}}\right)$$

则由

$$\left(\frac{\mathrm{d} r}{\mathrm{d} t}\right)^{2}=\left(\frac{\mathrm{d} r}{\mathrm{d} \tau}\right)^{2}\left(\frac{\mathrm{d} \tau}{\mathrm{d} t}\right)^{2}$$

可得

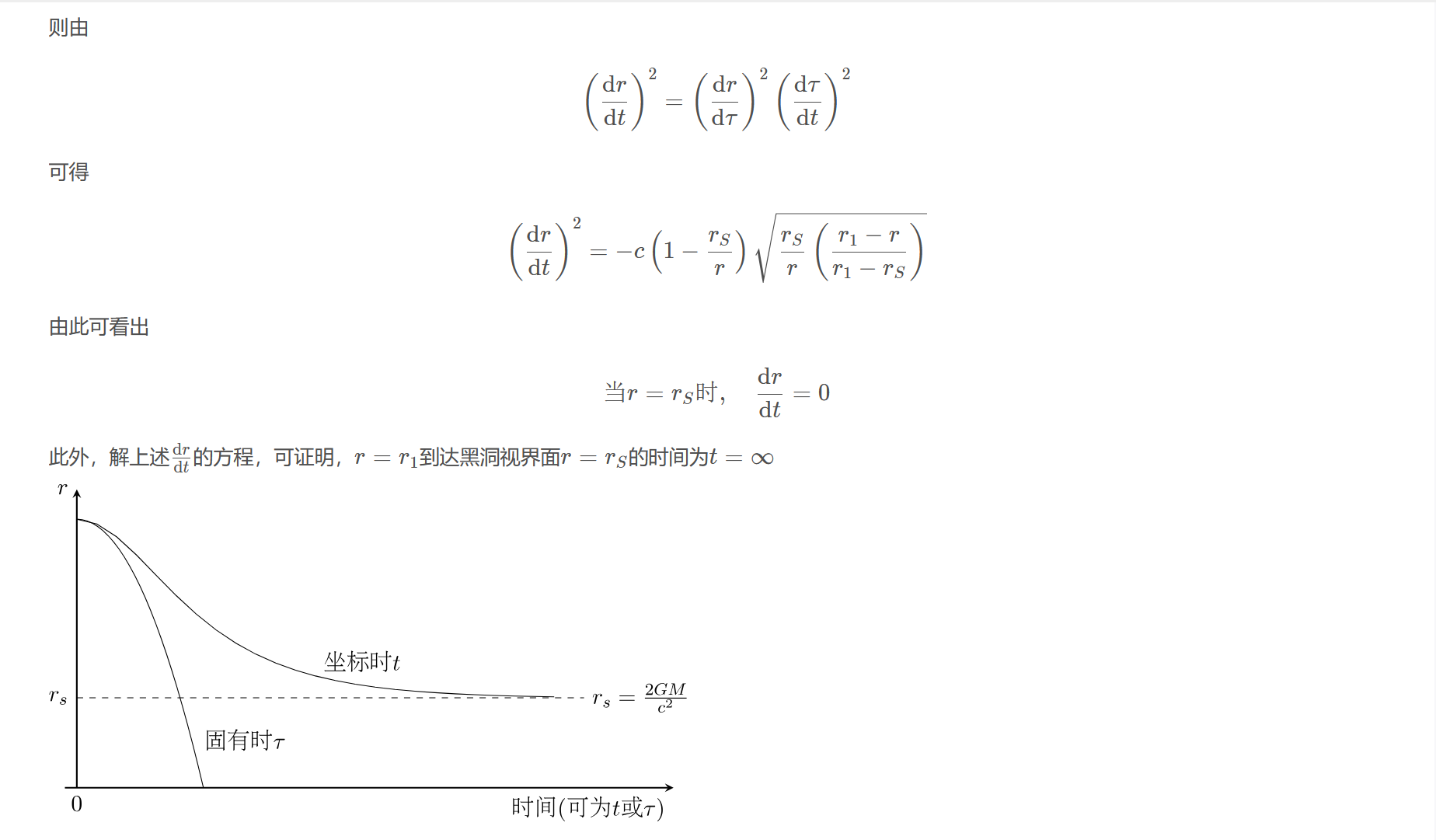
$$\left(\frac{\mathrm{d} r}{\mathrm{d} t}\right)^{2}=-c\left(1-\frac{r_{S}}{r}\right) \sqrt{\frac{r_{S}}{r}\left(\frac{r_{1}-r}{r_{1}-r_{S}}\right)}$$

由此可看出

$$\text{当}r=r_{S} \text{时},\quad \frac{\mathrm{d} r}{\mathrm{d} t}=0$$

此外，解上述$\frac{\mathrm{d}r}{\mathrm{d}t}$的方程，可证明，$r=r_{1}$到达黑洞视界面$r=r_{S}$的时间为$t=\infty$

4. Schwarzchild度规时间的奇点

由Schwarzschild度规

$$\begin{aligned} g_{00}=-\left(1-\frac{2 G M}{c^{2} r}\right) &, g_{11}=\frac{1}{1-\frac{2 G M}{c^{2} \tau}} \\ g_{22}=r^{2}, & g_{33}=r^{2} \sin \theta \end{aligned}$$

$$x^{0}=c t, \quad x^{1}=r \quad, \quad x^{2}=\theta, \quad x^{3}=\phi$$

可求出

$$\begin{aligned} R_{0101} &=-\frac{2 G M}{c^{2} r^{3}} \\ R_{0202} &=R_{0303}=\frac{G M}{c^{2} r^{3}} \\ R_{232 3} &=\frac{2 G M}{c^{2} r^{3}} \\ R_{1212} &=R_{1313}=-\frac{G M}{c^{2} r^{3}} \end{aligned}$$

真正奇点

$$r=0$$

5. 其它黑洞类型

恒星主要参数：

$$\begin{aligned}&M\text{——质量}\\&L\text{——自旋角动量}\\&Q\text{——电荷}\end{aligned}$$

度规仅决定于$M,L,Q$。

(1) $M\neq 0, L=0, Q=0$，Schwarschild度规

(2) $M\neq 0, L=0, Q\neq0$，Reissner-Nordstrom度规

(3) $M\neq 0, L\neq0, Q=0$，Kerr度规

(4) $M\neq 0, L\neq0, Q\neq0$，Kerr-Newman度规

Kerr-Newman黑洞视界

$$r_{+}=\frac{GM}{c^{2}}+\left(\frac{G^{2}M^{2}}{c^{4}}-\frac{G^{2}Q^{2}}{c^{8}}-a^{2}\right)^{\frac{1}{2}},\quad a=\frac{L}{Mc}$$

其中，"+"代替了各种度规i，是一个普遍的视界。

黑洞无毛定理: 黑洞的特征仅由$M,L,Q$决定。