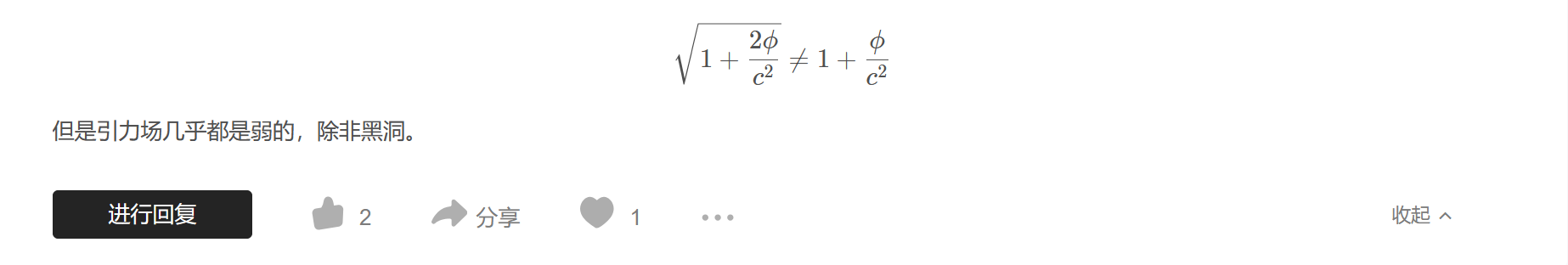物理

【广义相对论速成版】3. 中心球对称解与新引力效应 3.5 固有时与引力频移

1. 固有时

固有时间隔的定义为

$$\mathrm{d}\tau=\frac{1}{c} \mathrm{d} s$$

$$\mathrm{d} s^{2}=-g_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}$$

$\mathrm{d}s$具有长度的量纲，固有时$\mathrm{d}\tau$具有时间的量纲。在弯曲时空中质点的运动方程

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} s^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} s} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} s}=0$$

故可用固有时来描述

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} \tau^{2}}+\Gamma_{\mu \nu} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} \tau} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} \tau}=0$$

$\dfrac{\mathrm{d}x^{\lambda}}{\mathrm{d}\tau}$和$\dfrac{\mathrm{d}^{2}x^{\lambda}}{\mathrm{d}\tau^{2}}(\lambda=1,2,3)$分别具有速度和加速度的量纲，在存在引力以外的外力时，质点得运动方程

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} \tau^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} \tau} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} \tau}=f^{\lambda}$$

$f^{\lambda}$是单位质量的外力

$$f^{\lambda}=\frac{F^{\lambda}}{m}$$

$F^{\lambda}$是外力，上述质点运动方程的解可表述为

$$x^{\mu}=x^{\mu}(\tau)$$

这个轨道称为世界线，因此$\tau$是质点在弯曲时空中客观存在的时间参数，即固有时是客观存在的。

时钟(计时器)是由质点群构成的某种特殊装置。也可以是某种机械装置，故时钟在引力场中的计时标准应以固有时为依据。理论上可以证明描述原子的Schr$\ddot{o}$dinger方程的时间参数也是固有时，因此原子钟的计时标准也是固有时。

固有时的重要特征：

(1) 固有时与坐标选择无关

$$\mathrm{d} \tau=\frac{1}{c} \mathrm{d} s,\quad \text{是不变量}$$

(2) 固有时间隔在时空不同点是不同的

$$\mathrm{d} \tau=\frac{1}{c} \sqrt{-g_{\mu\nu} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} t} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} t}} \mathrm{d} t, \quad g_{\mu \nu}=g_{\mu \nu}(x)$$

(3) 固有时间隔与经历的路径有关

$$x^{\mu}=x^{\mu}(t)$$

$$\tau_{A B}=\frac{1}{c} \int_{A}^{B} \mathrm{d} s=\frac{1}{c} \int \sqrt{-g_{\mu \nu} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} t} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} t}} \mathrm{d} t$$

与$x^{\mu}=x^{\mu}(t)$有关，沿$c_{1}$和$c_{2}$两条不同的曲线，即使初始点$A$与终点$B$相同，$\tau_{AB}$也不一定相同。

2. 静态引力场中空间同一点两事件间的固有时间隔

静态引力场$g_{\mu\nu}$与$t$无关，空间同一点

$$\mathrm{d} x^{1}=\mathrm{d} x^{2}=\mathrm{d} x^{3}=0$$

故

$$\mathrm{d} \tau=\frac{1}{c} \sqrt{-g_{\mu \nu} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} t} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} t}} \mathrm{d} t=\frac{1}{c} \sqrt{-g_{00} \frac{\mathrm{d} x^{0}}{\mathrm{d} t} \frac{\mathrm{d} x^{0}}{\mathrm{d} t}} \mathrm{d} t, \quad x^{0}=c t$$

即

$$\mathrm{d} \tau=\sqrt{-g_{00}} \mathrm{d} t, \quad g_{00}=g_{00}\left(x^{1}, x^{2}, x^{3}\right)$$

假设在空间某一点发生两个事件，其坐标时的间隔为$t$，由于$g_{00}$与$t$无关，则这两事件的固有时间隔为

$$\tau=\sqrt{-g_{00} t}$$

$\tau$仅与空间点的位置有关。

如果在空间$p_{1}$和$p_{2}$两不同点发生两个坐标时间间隔相同的两事件，则不同点$p_{1}$和$p_{2}$两事件的固有时间隔

$$\tau_{1}=\tau\left(p_{1}\right) \quad , \quad \tau_{2}=\tau\left(p_{2}\right)$$

$$\tau_{1}=\tau\left(p_{1}\right)=\sqrt{-\left(g_{00}\right)_{1}} t \quad, \quad \tau_{2}=\tau\left(p_{2}\right)=\sqrt{-\left(g_{00}\right)_{2} t}$$

故

$$\frac{\tau_{1}}{\tau_{2}}=\frac{\sqrt{-\left(g_{00}\right)_{1}}}{\sqrt{-\left(g_{00}\right)_{2}}}$$

由于

$$g_{00}=-\left(1+\frac{2 \phi}{c^{2}}\right)$$

则

$$\frac{\tau_{1}}{\tau_{2}}=\frac{\sqrt{\left(1+\frac{2 \phi_{1}}{c^{2}}\right)}}{\sqrt{\left(1+\frac{2 \phi_{2}}{c^{2}}\right)}}$$

(在球引力源的特殊情况$\phi=-\frac{GM}{r}$。)在弱引力场近似下

$$\frac{\tau_{1}}{\tau_{2}}=\frac{\left(1+\frac{\phi_{1}}{c^{2}}\right)}{\left(1+\frac{\phi_{2}}{c^{2}}\right)}=1+\frac{1}{c^{2}}\left(\phi_{1}-\phi_{2}\right)$$

由于$\phi<0$，即

$$\phi=-|\phi|$$

$$\frac{\tau_{1}}{\tau_{2}}=1-\frac{1}{c^{2}}\left(\left|\phi_{1}\right|-\left|\phi_{2}\right|\right)$$

若$|\phi_{1}|>|\phi_{2}|$，则

$$\tau_{1}<\tau_{2}$$

故在太阳表面上的钟比地球上的钟走得慢，地面上的钟比高空的钟走得慢。广义相对论认为：

$$\boxed{时空弯曲的地方比平直慢}$$

弯曲越厉害，钟走得越慢。

3. 光波的引力频移

设原子发射一列波，在坐标时间间隔$t$内波数为$n$，这一列波由$P_{1}$传播到$P_{2}$点，则知

$$n=\tau v$$

是一个不变量。

设对应$t$在$P_{1}$处的固有时间隔为$\tau_{1}$，在$P_{2}$处的固有时间隔为$\tau_{2}$，由于$n$不变，故

$$n=\tau_{1} \nu_{1}=\tau_{2} \nu_{2}$$

$\nu_{1}$为光源$P_{1}$处发出光波的固有频率，$\nu_{2}$为$P_{2}$出观测者测得频率，故

$$\frac{\nu_{2}}{\nu_{1}}=\frac{\tau_{1}}{\tau_{2}}=1+\frac{1}{c^{2}}\left(\phi_{1}-\phi_{2}\right)$$

$$\frac{\nu_{2}}{\nu_{1}}=1-\frac{1}{c^{2}}\left(\left|\phi_{1}\right|-\left|\phi_{2}\right|\right)$$

$$\frac{\Delta \nu}{\nu_{1}}=\frac{\nu_{2}-\nu_{1}}{\nu_{1}}=-\frac{1}{c^{2}}\left(\left|\phi_{1}\right|-\left|\phi_{2}\right|\right)$$

故

- 若$|\phi_{1}|>|\phi_{2}|$，则$\nu_{2}<\nu_{1}$，即$\lambda_{2}>\lambda_{1}$，在$P_{2}$处观察到红移。

- 若$|\phi_{1}|<|\phi_{2}|$，则$\nu_{2}>\nu_{1}$，即$\lambda_{2}<\lambda_{1}$，在$P_{2}$处观测到紫移。

因此光由强引力场传播至弱引力场处，则在弱引力场处观测到红移现象。

4. 观测恒星谱线红移

设$P_{1}$点在恒星上，$P_{2}$点在地球上

$$\phi=-\frac{G M}{r}$$

在恒星$P_{1}$上

$$\phi_{1}=-\frac{G M_{1}}{R_{1}}$$

在地球$P_{2}$上

$$\phi_{2}=-\frac{G M_{2}}{R_{2}}$$

$$\left|\phi_{1}\right| \gg\left|\phi_{2}\right|$$

$$\frac{\nu_{2}-\nu_{1}}{\nu_{1}}=-\frac{1}{c^{2}}\left(\left|\phi_{1}\right|-\left|\phi_{2}\right|\right) \simeq-\frac{1}{c^{2}}\left|\phi_{1}\right|$$

即

$$\frac{\nu_{2}-\nu_{1}}{\nu_{1}}=-\frac{G M_{1}}{c^{2} R_{1}}$$

天文学中定义红移量

$$Z=-\frac{\Delta v}{\nu_{1}} \quad, \quad \Delta \nu=\nu_{2}-\nu_{1}$$

$$Z=\frac{G M_{1}}{c^{2} R_{1}}$$

对太阳

$$Z=\frac{G M_{\odot}}{c^{2} R_{\odot}} \quad, \quad M_{\odot}=1.983 \times 10^{33} \mathrm{g} \quad, \quad R_{\odot}=6.95 \times 10^{10} \mathrm{cm}$$

得理论值

$$Z=-\frac{\triangle \nu}{\nu_{1}}=\frac{G M_{\odot}}{c^{2} R_{\odot}}=2.12 \times 10^{-6}$$

1959年，M. G. Adam测得

$$Z=2 \times 10^{-6}$$

1961年，J. E. Blamont和E.Roddier及1963年J. Bault测得

$$Z=\left(2.12 \times 10^{-6}\right) \times(1.05 \pm 0.05)$$

5. 用Mössbauer谱仪在地面上测引力频移

以Co$^{57}$为源发射$14.4$KeV的$\gamma$射线，发射源置于地面高$h_{1}$处，以Fe$^{57}$在地面上$h_{2}$处共振吸收，利用Mössbauer谱仪共振吸收

$$h_{1}>h_{2}$$

$$\phi=-\frac{G M}{R+h}=-\frac{G M}{R} \cdot \frac{1}{1+\frac{h}{R}}=-\frac{G M}{R}\left(1-\frac{h}{R}\right)=-\frac{G M}{R}+\frac{G M h}{R^{2}}$$

$$\frac{\Delta \nu}{\nu_{1}}=\frac{\nu_{2}-\nu_{1}}{\nu_{1}}=\frac{1}{c^{2}}\left(\phi_{1}-\phi_{2}\right)=\frac{1}{c^{2}} \frac{G M}{R^{2}}\left(h_{1}-h_{2}\right)$$

$$h_{1}>h_{2}$$

$$\frac{\Delta \nu}{\nu_{1}}=\frac{1}{c^{2}} \frac{G M}{R^{2}}\left(h_{1}-h_{2}\right)>0$$

实际上$\frac{GM}{R^{2}}$为地面上的重力加速度

$$\frac{\Delta \nu}{\nu_{1}}=\frac{1}{c^{2}} g H$$

$$\nu_{2}>\nu_{1} \quad, \quad h_{1}>h_{2}$$

应观测到$\gamma$射线的紫移。

1960年，Pound和Rebka取$H=22.6m$，得理论值：

$$\frac{\Delta \nu}{\nu_{1}}=2.48 \times 10^{-15}$$

实验观测

$$\frac{\Delta \nu}{\nu_{1}}=(2.57 \pm 0.26) \times 10^{-15}$$

与理论值符合很好。这证明了的确有紫移。

6. 引力频移不能验证广义相对论

这是由于频移公式可由光子在引力场中的能量守恒直接证明。

在引力场中的能量守恒定律可表述为

$$h \nu_{1}+m_{1} \phi_{1}=h \nu_{2}+m_{2} \phi_{2},\quad \phi\text{为引力势}$$

光子质量(无静止质量)

$$m_{1}=\frac{h \nu_{1}}{c^{2}} \quad, \quad m_{2}=\frac{h \nu_{2}}{c^{2}}$$

则

$$h \nu_{1}+\frac{h \nu_{1}}{c^{2}} \phi_{1}=h \nu_{2}+\frac{h \nu_{2}}{c^{2}} \phi_{2}$$

由此可知

$$\nu_{1}\left(1+\frac{\phi_{1}}{c^{2}}\right)=\nu_{2}\left(1+\frac{\phi_{2}}{c^{2}}\right)$$

可得

$$\frac{\nu_{2}}{\nu_{1}}=\frac{1+\frac{\phi_{1}}{c^{2}}}{1+\frac{\phi_{2}}{c^{2}}}=1+\frac{1}{c^{2}}\left(\phi_{1}-\phi_{2}\right)$$

故

$$\frac{\Delta \nu}{\nu_{1}}=\frac{1}{c^{2}}\left(\phi_{1}-\phi_{2}\right)$$

即以前得到的频移公式。只有强引力势$\phi$时才能验证广义相对论

$$\sqrt{1+\frac{2 \phi}{c^{2}}} \neq 1+\frac{\phi}{c^{2}}$$

但是引力场几乎都是弱的，除非黑洞。