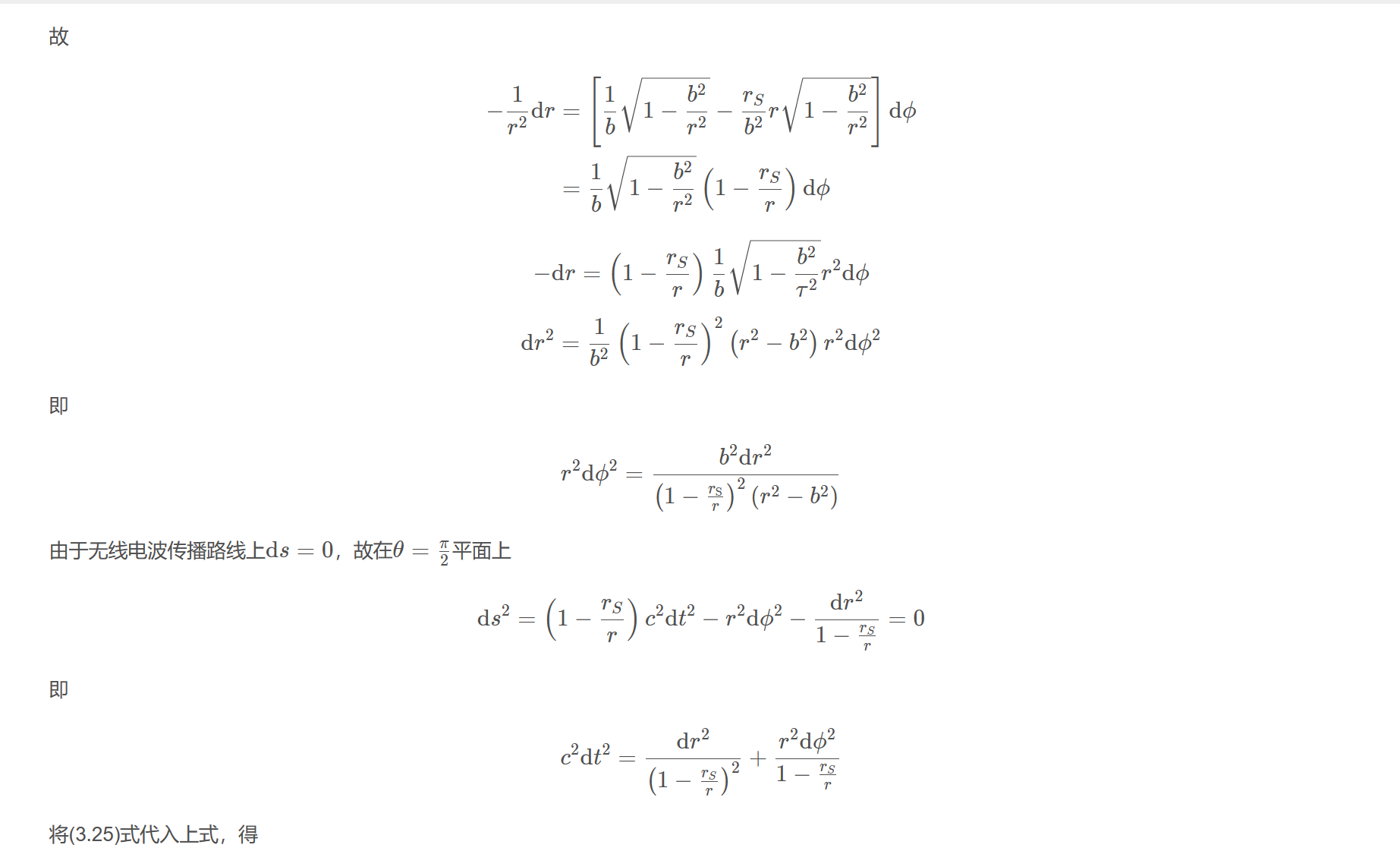物理

【广义相对论速成版】3. 中心球对称解与新引力效应 3.4 雷达回波延迟

1964年Irwin I. Shaprio提出行星的雷达回波存在延迟效应，可以验证广义相对论。1968年以后进行了多次雷达回波时延，证实了上述效应的存在。$r_{1}$为地球到太阳的距离，$r_{2}$为反射星到太阳的距离。

设雷达信号在$\theta=\frac{\pi}{2}$平面内自$(r_{1},\phi_{1})$处由地球发射雷达波到$(r_{2},\phi_{2})$处反射星，由于雷达波$\mathrm{d}s^{2}=0$，其传播线满足方程

$$u=\frac{1}{b} \sin \phi+\frac{G M}{c^{2} b^{2}}\left(\cos ^{2} \phi + 1\right)$$

即

$$\frac{1}{r}=\frac{1}{b} \sin \phi+\frac{1}{2} \frac{r_{S}}{b^{2}}\left(\cos ^{2} \phi+1\right), \quad r_{S}=\frac{2 G M}{c^{2}}\tag{3.25}$$

则

$$-\frac{1}{r^{2}} \mathrm{d} r=\frac{1}{b}\left[\cos \phi-\frac{r_{S}}{b} \sin \phi \cos \phi\right] \mathrm{d} \phi$$

取近似

$$\sin \phi=\frac{b}{r}, \quad \cos \phi=\sqrt{1-\frac{b^{2}}{r^{2}}}$$

故

$$\begin{aligned}-\frac{1}{r^{2}} \mathrm{d} r &=\left[\frac{1}{b} \sqrt{1-\frac{b^{2}}{r^{2}}}-\frac{r_{S}}{b^{2}} r \sqrt{1-\frac{b^{2}}{r^{2}}}\right] \mathrm{d} \phi \\ &=\frac{1}{b}\sqrt{1-\frac{b^{2}}{r^{2}}}\left(1-\frac{r_{S}}{r}\right) \mathrm{d} \phi\end{aligned}$$

$$-\mathrm{d} r=\left(1-\frac{r_{S}}{r}\right) \frac{1}{b} \sqrt{1-\frac{b^{2}}{\tau^{2}}} r^{2} \mathrm{d} \phi$$

$$\mathrm{d} r^{2}=\frac{1}{b^{2}}\left(1-\frac{r_{S}}{r}\right)^{2}\left(r^{2}-b^{2}\right) r^{2} \mathrm{d} \phi^{2}$$

即

$$r^{2} \mathrm{d} \phi^{2}=\frac{b^{2} \mathrm{d} r^{2}}{\left(1-\frac{r_{\mathrm{S}}}{r}\right)^{2}\left(r^{2}-b^{2}\right)}$$

由于无线电波传播路线上$\mathrm{d}s=0$，故在$\theta=\frac{\pi}{2}$平面上

$$\mathrm{d} s^{2}=\left(1-\frac{r_{S}}{r}\right) c^{2} \mathrm{d} t^{2}-r^{2} \mathrm{d} \phi^{2}-\frac{\mathrm{d} r^{2}}{1-\frac{r_{S}}{r}}=0$$

即

$$c^{2} \mathrm{d} t^{2}=\frac{\mathrm{d} r^{2}}{\left(1-\frac{r_{S}}{r}\right)^{2}}+\frac{r^{2} \mathrm{d} \phi^{2}}{1-\frac{r_{S}}{r}}$$

将(3.25)式代入上式，得

$$\begin{aligned}c^{2} \mathrm{d} t^{2} &=\frac{\mathrm{d} r^{2}}{\left(1-\frac{r_{S}}{r}\right)^{2}} \frac{b^{2} \mathrm{d} r^{2}}{\left(1-\frac{r_{S}}{\tau}\right)^{3}\left(r^{2}-b^{2}\right)} \\ &=\frac{\mathrm{d} r^{2}}{\left(1-\frac{r s}{r}\right)^{2}}\left[1+\frac{b^{2}}{\left(1-\frac{r_{S}}{r}\right)\left(r^{2}-b^{2}\right)}\right] \\ &=\frac{\mathrm{d} r^{2}}{\left(1-\frac{r_{S}}{r}\right)^{2}}\left[\frac{\left(1-\frac{r_{S}}{r}\right)\left(r^{2}-b^{2}\right)+b^{2}}{\left(1-\frac{r_{S}}{r}\right)\left(r^{2}-b^{2}\right)}\right] \end{aligned}$$

由此可得

$$\begin{aligned}c \mathrm{d} t &=\frac{\mathrm{d} r}{\left(1-\frac{r_{S}}{r}\right)}\left[\frac{r^{2}-b^{2}-r r_{S}+\frac{r_{s} b^{2}}{r}+b^{2}}{\left(1-\frac{r_{S}}{r}\right)\left(r^{2}-b^{2}\right)}\right]^{\frac{1}{2}} \\ &=\frac{r \mathrm{d} r\left(1-\frac{r_{S}}{r}+\frac{r_{S}}{r^{3}} b^{2}\right)^{\frac{1}{2}}}{\left(1-\frac{r_{S}}{r}\right)^{\frac{3}{2}} \sqrt{r^{2}-b^{2}}} \end{aligned}$$

取$\frac{r_{s}}{r}$一阶小量

$$c \mathrm{d}     t=\frac{r \mathrm{d} r\left[1-\frac{1}{2} \cdot \frac{r_{S}}{r}+\frac{1}{2} \cdot \frac{r_{S}}{r^{3}} b^{2}\right]}{\left(1-\frac{3}{2} \cdot \frac{r_{S}}{r}\right) \sqrt{r^{2}-b^{2}}}$$

进一步得到

$$\begin{aligned}c \mathrm{d} t &=\frac{r \mathrm{d} r}{\sqrt{r^{2}-b^{2}}}\left[1-\frac{1}{2} \cdot \frac{r_{S}}{r}+\frac{1}{2} \cdot \frac{r_{S}}{r^{3}} b^{2}+\frac{3}{2} \cdot \frac{r_{S}}{r}\right] \\ &=\frac{r \cdot \mathrm{d} r}{\sqrt{r^{2}-b^{2}}}\left[1+\frac{r_{S}}{r}+\frac{1}{2} \cdot \frac{r_{S}}{r^{3}} b^{2}\right]\end{aligned}$$

即

$$c \mathrm{d} t=\frac{r \mathrm{d} r}{\sqrt{r^{2}-b^{2}}}+r_{S} \frac{\mathrm{d} r}{\sqrt{r^{2}-b^{2}}}+\frac{1}{2} r_{S} b^{2} \frac{\mathrm{d} r}{r^{2} \sqrt{r^{2}-b^{2}}}\tag{3.26}$$

由于

- 当$r$在$r_{1}\to b$区间，$\mathrm{d}r<0$

- 当$r$在$b\to r_{2}$区间，$\mathrm{d}r>0$

故由$r_{1}\to r_{2}$的积分相当于$b\to r_{1}$的积分与$b\to r_{2}$的积分之和。利用积分公式

$$\int \frac{r \mathrm{d} r}{\sqrt{r^{2}-b^{2}}}=\sqrt{r^{2}-b^{2}}$$

$$\int \frac{\mathrm{d} r}{\sqrt{r^{2}-b^{2}}}=\ln \left[r+\sqrt{r^{2}-b^{2}}\right]$$

$$\int \frac{\mathrm{d} r}{r^{2} \sqrt{r^{2}-b^{2}}}=\frac{1}{b^{2} r} \sqrt{r^{2}-b^{2}}$$

定义

$$t(b \rightarrow r)=\int_{b}^{r} c \mathrm{d} t$$

对(3.26)积分得

$$t(b \rightarrow r)=\sqrt{r^{2}-b^{2}}+r_{S} \ln \frac{r-\sqrt{r^{2}-b^{2}}}{b} +\frac{1}{2} \cdot \frac{r_{S}}{r} \sqrt{r^{2}-b^{2}}$$

故

$$t\left(r_{1} \rightarrow r_{2}\right)=t\left(b \rightarrow r_{1}\right)+t\left(b \rightarrow r_{2}\right)$$

令$T$为$r_{1}\to r_{2}$的时间

$$\begin{aligned}c T=&\sqrt{r_{1}^{2}-b^{2}}+\sqrt{r_{2}^{2}-b^{2}}+r_{S} \ln \frac{r_{1}+\sqrt{r_{1}^{2}-b^{2}}}{b}+r_{S} l n \frac{r_{2}+\sqrt{r_{2}^{2}-b^{2}}}{b}\\&+\frac{1}{2} \cdot \frac{r_{S}}{r_{1}} \sqrt{r_{1}^{2}-b^{2}}+\frac{1}{2} \cdot \frac{r_{S}}{r_{2}} \sqrt{r_{2}^{2}-b^{2}}\end{aligned}$$

即

$$\begin{aligned}T=&\left[\sqrt{r_{1}^{2}-b^{2}}+\sqrt{r_{2}^{2}-b^{2}}+r_{S}\ln\left(\frac{r_{2}+\sqrt{r_{2}^{2}-b^{2}}}{b}\right)\left(\frac{r_{1}+\sqrt{r_{1}^{2}-b^{2}}}{b}\right)\right.\\ &\left.+\frac{r_{S}}{2} \left(\cdot \frac{1}{r_{1}} \sqrt{r_{1}^{2}-b^{2}}+\frac{1}{r_{2}} \sqrt{r_{2}^{2}-b^{2}}\right)\right]\end{aligned}$$

故雷达波去和返回的总时间为

$$T_{\text{total}}=2 T$$

由于$r_{1}$和$r_{2}$远大于$b$，则

$$\text{当}r=r_{1},\text{或}r=r_{2}\text{时},\quad \sqrt{r^{2}-b^{2}}=r$$

故

$$T_{\text { total }}=\frac{2}{c}\left[r_{1}+r_{2}+r_{S} \ln \frac{4 r_{1} r_{2}}{b^{2}}+r_{S}\right]$$

无广义相对论引力效应时，去和回波的时间为

$$\frac{2 \ell}{c}=\frac{2\left(r_{1}+r_{2}\right)}{c}$$

因此存在雷达去和回波延迟时间

$$\Delta T=\frac{2 r_{S}}{c}\left[1+\ln \frac{4 r_{1} r_{2}}{b^{2}}\right]$$

代入

$$r_{S}=\frac{2 G N_{M}}{c^{2}}$$

得

$$\Delta T=\frac{4 G M}{c^{3}}\left[1+\ln \frac{4 r_{1} r_{2}}{b^{2}}\right]$$

在太阳引力中进行实验，且雷达去和返回时传播经太阳边缘，则

$$M=\lambda_{\odot} \quad, \quad b=R_{\odot}$$

故

$$\Delta T=\frac{4 G M_{\odot}}{c^{3}}\left[1+\ln \frac{4 r_{1} r_{2}}{R_{\odot}^{2}}\right] $$

对水星的回波观测，$r_{2}$为水星到太阳的距离，即水星为反射星，理论计算得

$$(\Delta T)_{\text { theory }}=240 \mu s=240 \times 10^{-6} s$$

1968年，Shapiro对水星测得

$$\frac{(\Delta T)_{\text {experiment}}}{(\Delta T)_{\text { theory }}}=0.9 \pm 0.02$$

1971年，Shapiro对金星测得

$$\frac{(\Delta T)_{\text { experiment }}}{(\Delta T)_{\text { theory }}}=1.02 \pm 0.05$$

1977年，J. D. Anderson等对人造行星水手VI和VII测得

$$\frac{(\Delta T)_{\text {experiment}}}{(\Delta T)_{\text { theory }}}=1.00 \pm 0.04$$