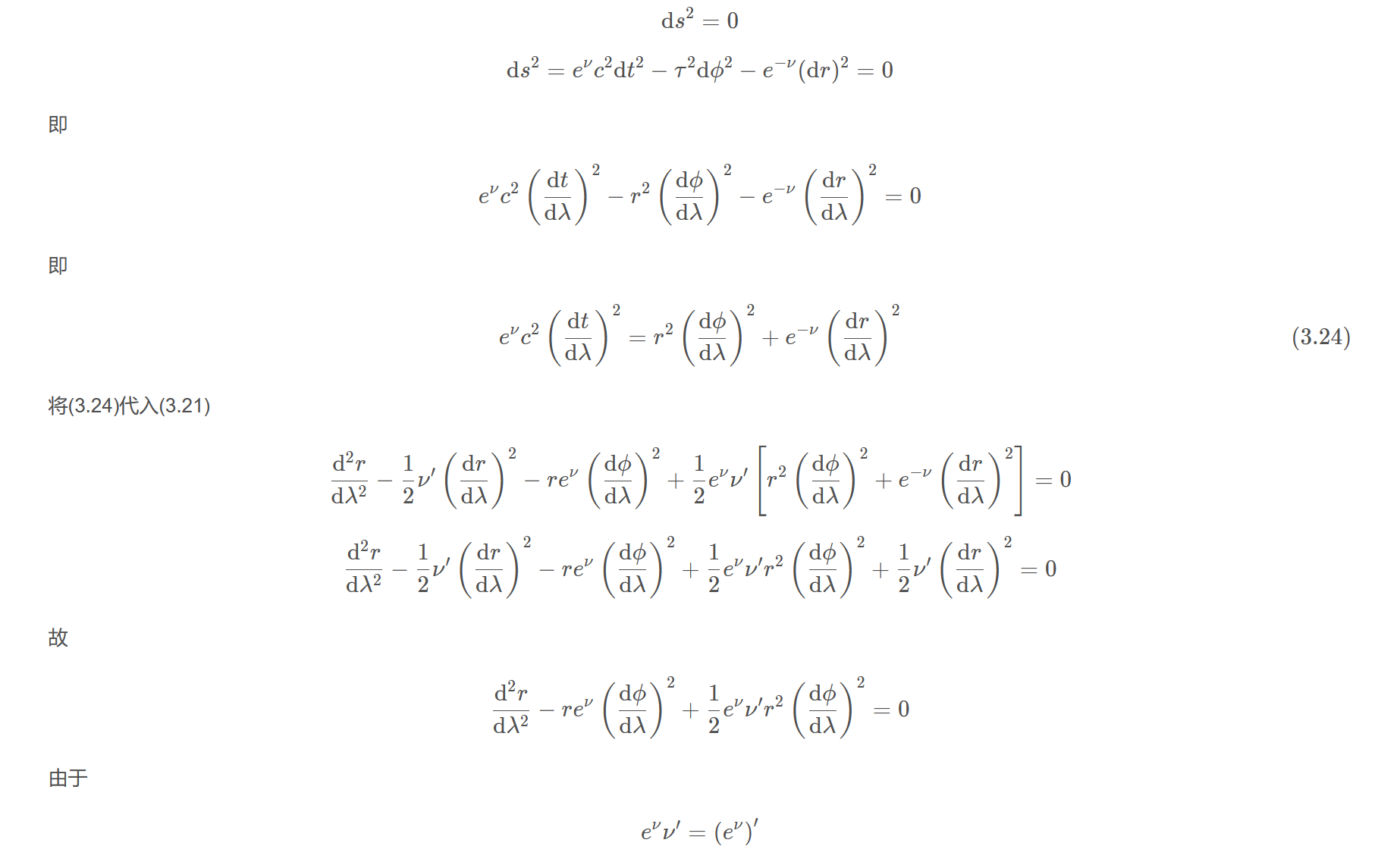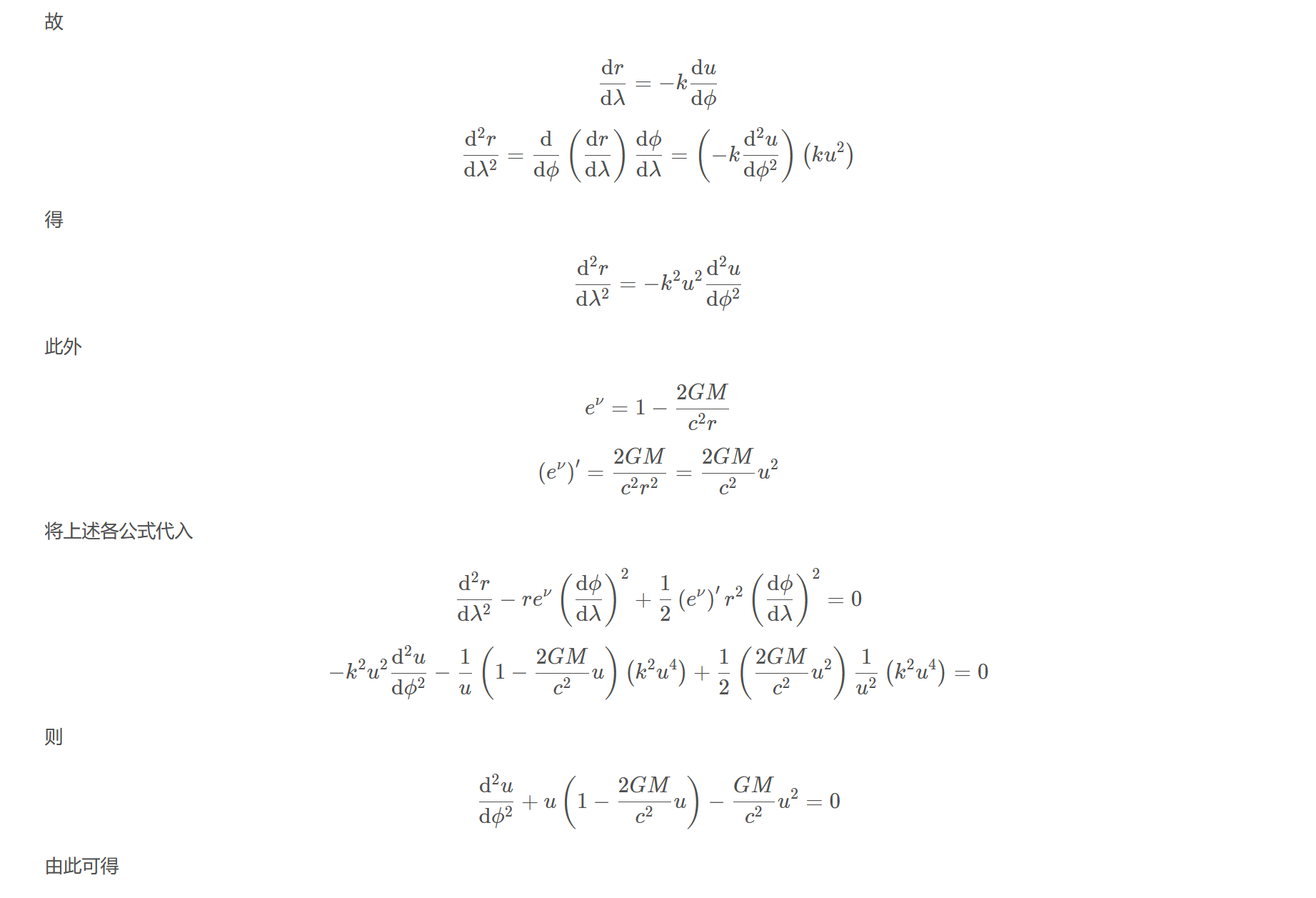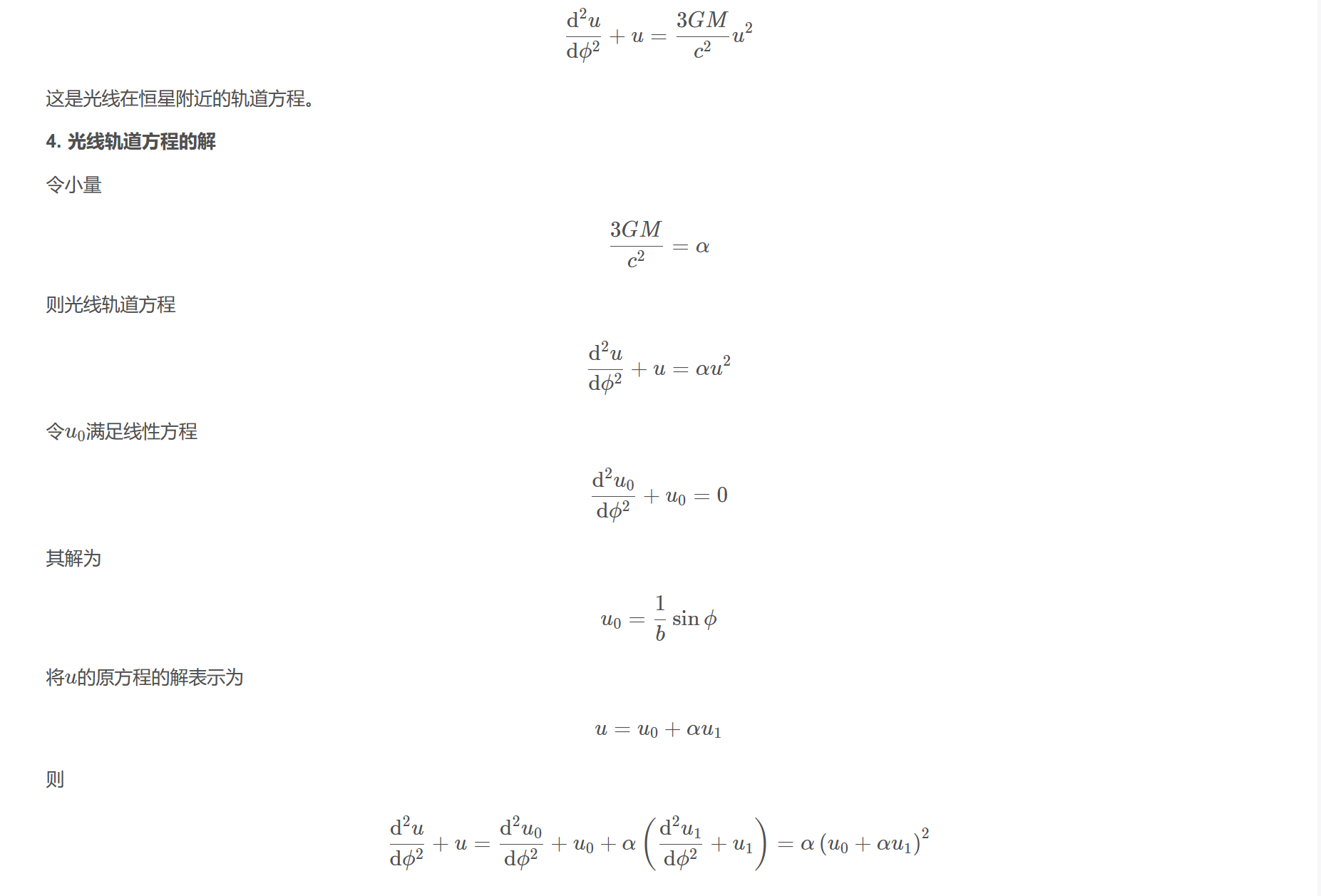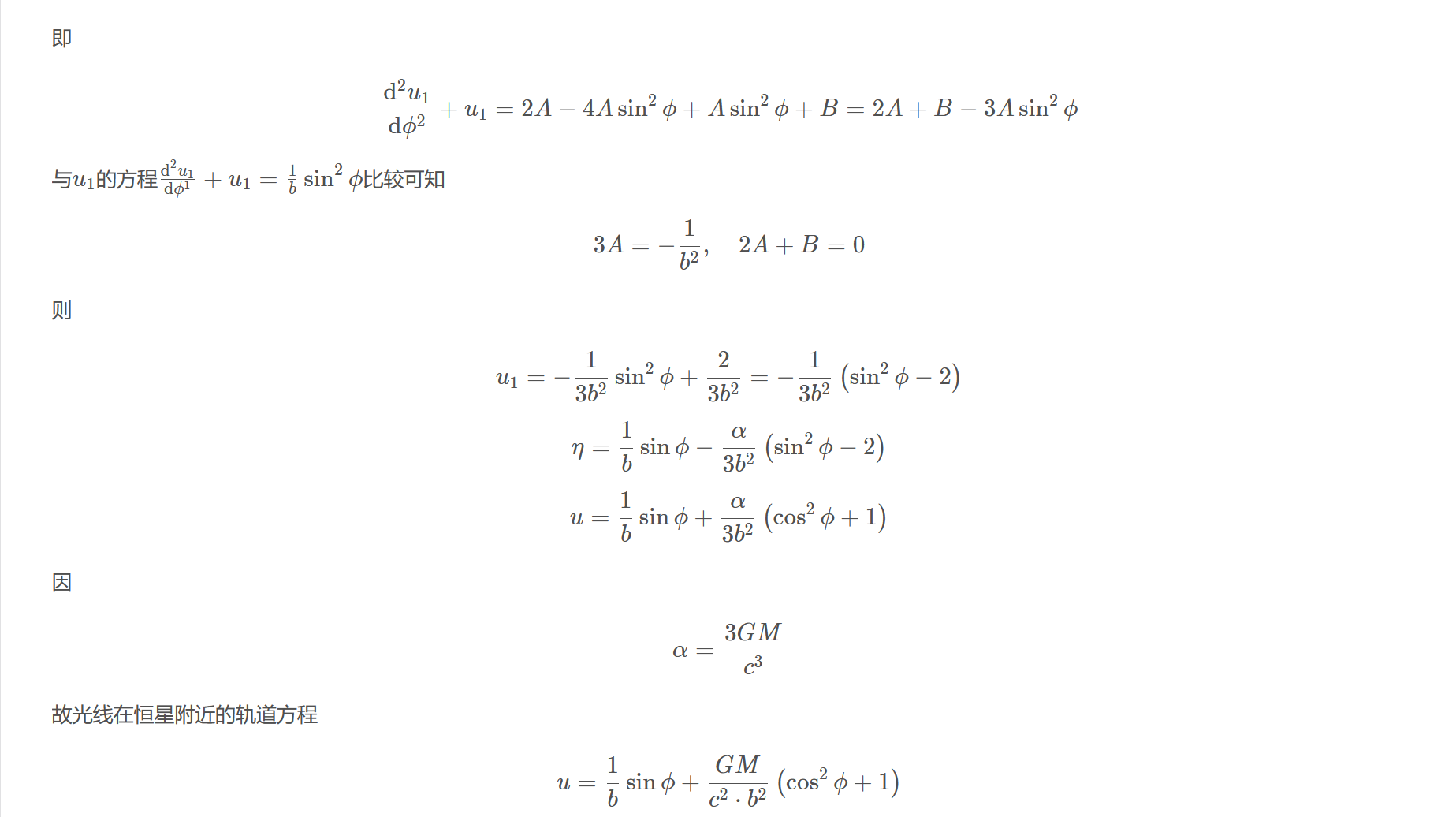物理 【广义相对论速成版】3. 中心球对称解与新引力效应 3.3 光线在恒星附近的偏折
1. 光波在引力场中的传播路线
具有静止质量$m$的粒子的$4-$动量矢量
$$p^{\mu}=m c u^{\mu}, \quad u^{\mu}=\frac{\mathrm{d} x^{\mu}}{\mathrm{d} s}=\frac{1}{c} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} \tau}$$
$\tau$为固有时。
$$\mathrm{d} s^{2}=-g_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}$$
$$g_{\mu \nu} u^{\mu} u^{\nu}=-1$$
$$p^{2}=g_{\mu \nu} p^{\mu} p^{\nu}=-m^{2} c^{2}$$
即
$$p^{2}+m^{2} c^{2}=0$$
粒子在弯曲时空中运动,$u^{\mu}$在运动轨迹上始终是平行的(或是平行场),即
$$\nabla_{\mu} u^{\lambda}=0$$
由此可导得短程线方程。
对光的传播,因光子静止质量$m=0$,公式
$$p^{\mu}=m c \frac{\mathrm{d} x^{\mu}}{\mathrm{d} s}$$
就存在问题了,必须要求$\mathrm{d}s=0$,也即光的传播路线不能用弧元$s$为参数($x^{\mu}=x^{\mu}(s)$)。可引入任意参数,定义光线的切矢波矢
$$K^{\mu}=\frac{\mathrm{d} x^{\mu}}{\mathrm{d} \lambda}, \quad x^{\mu}=x^{\mu}(\lambda)$$
由于
$$\mathrm{d} s^{2}=0$$
易知
$$K^{2}=g_{\mu \nu} K^{\mu} K^{\nu}=0$$
并进一步假设切矢$K^{\mu}$在光线传播的路线上是平行的,即
$$\nabla_{\mu} K^{\lambda}=0$$
故
$$K^{\mu} \nabla_{\mu} K^{\lambda}=0$$
即
$$K^{\mu}\left(\partial_{\mu} K^{\lambda}+\Gamma_{\mu \nu}^{\lambda} K^{\nu}\right)=0$$
$$K^{\mu} \partial_{\mu} K^{\lambda}=\frac{\mathrm{d} x^{\mu}}{\mathrm{d} \lambda} \frac{\partial K^{\lambda}}{\partial x^{\mu}}=\frac{\mathrm{d} K^{\lambda}}{\mathrm{d} \lambda}$$
故
$$\frac{\mathrm{d} K^{\lambda}}{\mathrm{d} \lambda}+\Gamma_{\mu \nu}^{\lambda} K^{\mu} K^{\nu}=0$$
代入
$$K^{\lambda}=\frac{\mathrm{d} x^{\lambda}}{\mathrm{d} \lambda}$$
得光线传播的路径方程
$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} \lambda^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} \lambda} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} \lambda}=0$$
这是一种特殊的“短程线”方程。
2. Schwarzchild解情况下的光传播方程
中心为恒星,度规为中心球对称情况下的光波传播路线的方程,应将过去中心球对称的短程线方程中进行$s\to\lambda$置换,即
$$\frac{\mathrm{d}^{2} r}{\mathrm{d} \lambda^{2}}-\frac{1}{2} \nu^{\prime}\left(\frac{\mathrm{d} r}{\mathrm{d} \lambda}\right)^{2}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+\frac{1}{2} e^{2 \nu} \nu^{\prime} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} \lambda}\right)^{2}=0\tag{3.21}$$
$$\frac{\mathrm{d}^{2} \phi}{\mathrm{d} \lambda^{2}}+\frac{2}{r} \frac{\mathrm{d} r}{\mathrm{d} \lambda} \frac{\mathrm{d} \phi}{\mathrm{d} \lambda}=0\tag{3.22}$$
$$e^{\nu}=1-\frac{2 G M}{c^{2} r}$$
方程(3.22)可以写成
$$r^{2} \frac{\mathrm{d}^{2} \phi}{\mathrm{d} \lambda^{2}}+2 r \frac{\mathrm{d} r}{\mathrm{d} \lambda} \frac{\mathrm{d} \phi}{\mathrm{d} \lambda}=0$$
即
$$\mathrm{d}\left(r^{2} \frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)=0$$
故
$$r^{2} \frac{\mathrm{d} \phi}{\mathrm{d} \lambda}=k, \quad k\text{为常数}\tag{3.23}$$
对光的传播(在$\theta=\frac{\pi}{2}$平面上)
$$\mathrm{d} s^{2}=0$$
$$\mathrm{d} s^{2}=e^{\nu} c^{2} \mathrm{d} t^{2}-\tau^{2} \mathrm{d} \phi^{2}-e^{-\nu}(\mathrm{d} r)^{2}=0$$
即
$$e^{\nu} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} \lambda}\right)^{2}-r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}-e^{-\nu}\left(\frac{\mathrm{d} r}{\mathrm{d} \lambda}\right)^{2}=0$$
即
$$e^{\nu} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} \lambda}\right)^{2}=r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+e^{-\nu}\left(\frac{\mathrm{d} r}{\mathrm{d} \lambda}\right)^{2}\tag{3.24}$$
将(3.24)代入(3.21)
$$\frac{\mathrm{d}^{2} r}{\mathrm{d} \lambda^{2}}-\frac{1}{2} \nu^{\prime}\left(\frac{\mathrm{d} r}{\mathrm{d} \lambda}\right)^{2}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+\frac{1}{2} e^{\nu} \nu^{\prime}\left[r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+e^{-\nu}\left(\frac{\mathrm{d} r}{\mathrm{d} \lambda}\right)^{2}\right]=0$$
$$\frac{\mathrm{d}^{2} r}{\mathrm{d} \lambda^{2}}-\frac{1}{2} \nu^{\prime}\left(\frac{\mathrm{d} r}{\mathrm{d} \lambda}\right)^{2}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+\frac{1}{2} e^{\nu} \nu^{\prime} r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+\frac{1}{2} \nu^{\prime}\left(\frac{\mathrm{d} r}{\mathrm{d} \lambda}\right)^{2}=0$$
故
$$\frac{\mathrm{d}^{2} r}{\mathrm{d} \lambda^{2}}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+\frac{1}{2} e^{\nu} \nu^{\prime} r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}=0$$
由于
$$e^{\nu} \nu^{\prime}=\left(e^{\nu}\right)^{\prime}$$
故
$$\frac{\mathrm{d}^{2} r}{\mathrm{d} \lambda^{2}}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+\frac{1}{2}\left(e^{\nu}\right)^{\prime} r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}=0$$
3. 引入$u=\frac{1}{r}$变量的光轨道方程
定义
$$u=\frac{1}{r}$$
则
$$\mathrm{d}^{\prime} u=-\frac{1}{r^{2}} \mathrm{d} r=-u^{2} \mathrm{d} r$$
即
$$\mathrm{d} r=-\frac{1}{u^{2}} \mathrm{d} u$$
(3.23)可化为
$$\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}=k u^{2}$$
且
$$\frac{\mathrm{d} r}{\mathrm{d} \phi}=-\frac{1}{u^{2}} \frac{\mathrm{d} u}{\mathrm{d} \phi}$$
则
$$\frac{\mathrm{d} r}{\mathrm{d} \lambda}=\frac{\mathrm{d} r}{\mathrm{d} \phi} \frac{\mathrm{d} \phi}{\mathrm{d} \lambda}=\left(-\frac{1}{u^{2}} \frac{\mathrm{d} u}{\mathrm{d} \phi}\right)\left(k u^{2}\right)$$
故
$$\frac{\mathrm{d} r}{\mathrm{d} \lambda}=-k \frac{\mathrm{d} u}{\mathrm{d} \phi}$$
$$\frac{\mathrm{d}^{2} r}{\mathrm{d} \lambda^{2}}=\frac{\mathrm{d}}{\mathrm{d} \phi}\left(\frac{\mathrm{d} r}{\mathrm{d} \lambda}\right) \frac{\mathrm{d} \phi}{\mathrm{d} \lambda}=\left(-k \frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}\right)\left(k u^{2}\right)$$
得
$$\frac{\mathrm{d}^{2} r}{\mathrm{d} \lambda^{2}}=-k^{2} u^{2} \frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}$$
此外
$$e^{\nu}=1-\frac{2 G M}{c^{2} r}$$
$$\left(e^{\nu}\right)^{\prime}=\frac{2 G M}{c^{2} r^{2}}=\frac{2 G M}{c^{2}} u^{2}$$
将上述各公式代入
$$\frac{\mathrm{d}^{2} r}{\mathrm{d} \lambda^{2}}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}+\frac{1}{2}\left(e^{\nu}\right)^{\prime} r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} \lambda}\right)^{2}=0$$
$$-k^{2} u^{2} \frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}-\frac{1}{u}\left(1-\frac{2 G M}{c^{2}} u\right)\left( k^{2} u^{4}\right)+\frac{1}{2}\left(\frac{2 G M}{c^{2}} u^{2}\right) \frac{1}{u^{2}}\left(k^{2} u^{4}\right)=0$$
则
$$\frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}+u\left(1-\frac{2 G M}{c^{2}} u\right)-\frac{G M}{c^{2}} u^{2}=0$$
由此可得
$$\frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}+u=\frac{3 G M}{c^{2}} u^{2}$$
这是光线在恒星附近的轨道方程。
4. 光线轨道方程的解
令小量
$$\frac{3 G M}{c^{2}}=\alpha$$
则光线轨道方程
$$\frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}+u=\alpha u^{2}$$
令$u_{0}$满足线性方程
$$\frac{\mathrm{d}^{2} u_{0}}{\mathrm{d} \phi^{2}}+u_{0}=0$$
其解为
$$u_{0}=\frac{1}{b} \sin \phi$$
将$u$的原方程的解表示为
$$u=u_{0}+\alpha u_{1}$$
则
$$\frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}+u=\frac{\mathrm{d}^{2} u_{0}}{\mathrm{d} \phi^{2}}+u_{0}+\alpha\left(\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}\right)=\alpha\left(u_{0}+\alpha u_{1}\right)^{2}$$
取$\alpha$一阶近似
$$\alpha\left(\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}\right)=\alpha u_{0}^{2}$$
即
$$\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}=u_{0}^{2}$$
将$u_{0}=\frac{1}{b}\sin\phi$代入
$$\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{2}=\frac{1}{b^{2}} \sin ^{2} \phi$$
令其解为
$$u_{1}=A \sin ^{2} \phi+B$$
则
$$\frac{\mathrm{d} u_{1}}{\mathrm{d} \phi}=2 A \sin \phi \cos \phi=A \sin 2 \phi$$
$$\frac{d^{2} u_{1}}{d \phi^{2}}=2 A \cos 2 \phi=2 A\left(1-2 \sin ^{2} \phi\right)=2 A-4 A \sin ^{2} \phi$$
故
$$\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}=2 A-4 A \sin ^{2} \phi+A \sin ^{2} \phi+B=2 A-3 A \sin ^{2} \phi+B$$
即
$$\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}=2 A-4 A \sin ^{2} \phi+A \sin ^{2} \phi+B=2 A+B-3 A \sin ^{2} \phi$$
与$u_{1}$的方程$\frac{\mathrm{d}^{2}u_{1}}{\mathrm{d}\phi^{1}}+u_{1}=\frac{1}{b}\sin^{2}\phi$比较可知
$$3 A=-\frac{1}{b^{2}}, \quad 2 A+B=0$$
则
$$u_{1}=-\frac{1}{3 b^{2}} \sin ^{2} \phi+\frac{2}{3 b^{2}}=-\frac{1}{3 b^{2}}\left(\sin ^{2} \phi-2\right)$$
$$\eta=\frac{1}{b} \sin \phi-\frac{\alpha}{3 b^{2}}\left(\sin ^{2} \phi-2\right)$$
$$u=\frac{1}{b} \sin \phi+\frac{\alpha}{3 b^{2}}\left(\cos ^{2} \phi+1\right)$$
因
$$\alpha=\frac{3 G M}{c^{3}}$$
故光线在恒星附近的轨道方程
$$u=\frac{1}{b} \sin \phi+\frac{G M}{c^{2} \cdot b^{2}}\left(\cos ^{2} \phi+1\right)$$
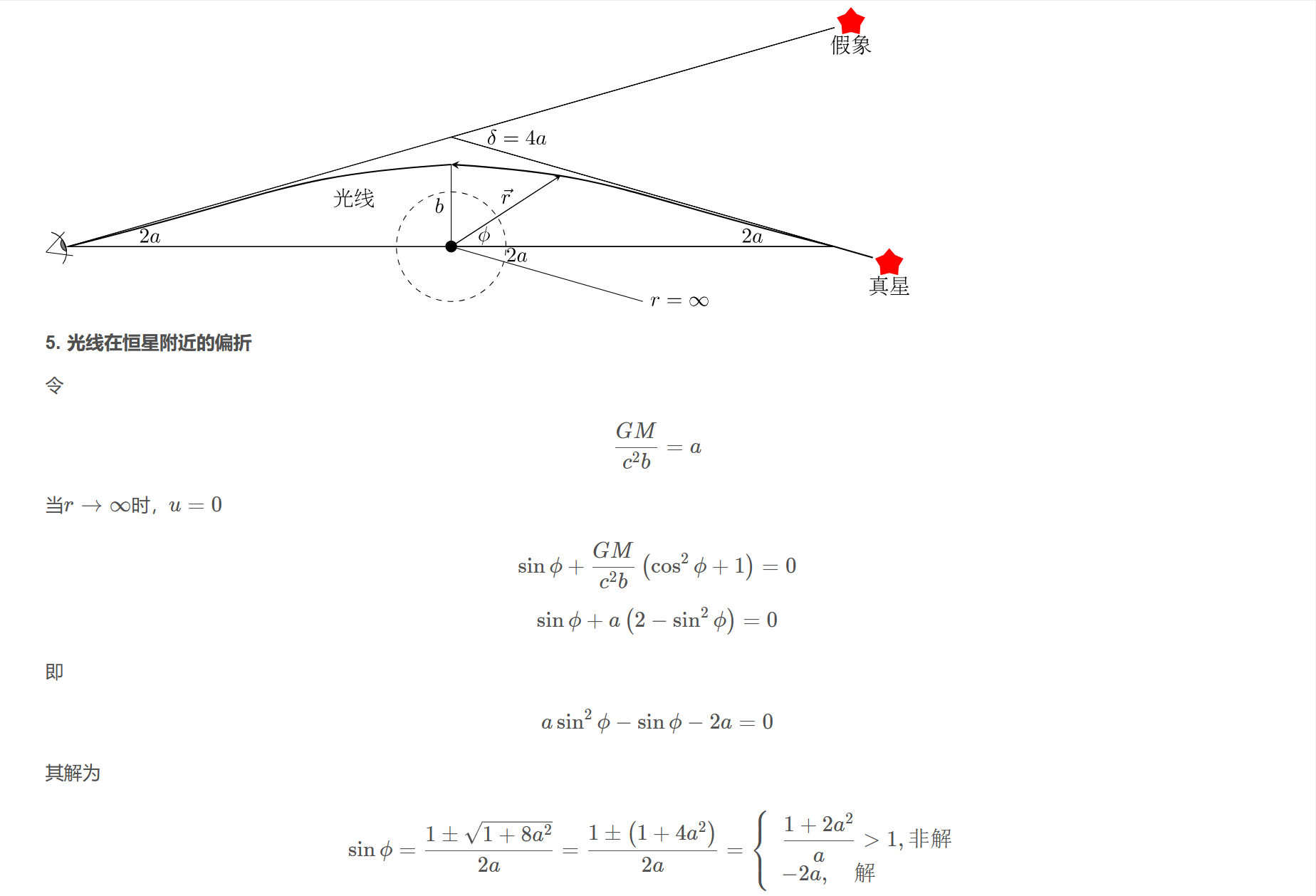
5. 光线在恒星附近的偏折
令
$$\frac{G M}{c^{2} b}=a$$
当$r\to\infty$时,$u=0$
$$\sin \phi+\frac{G M}{c^{2} b}\left(\cos ^{2} \phi+1\right)=0$$
$$\sin \phi+a\left(2-\sin ^{2} \phi\right)=0$$
即
$$a \sin ^{2} \phi-\sin \phi-2 a=0$$
其解为
$$\sin \phi=\frac{1 \pm \sqrt{1+8 a^{2}}}{2 a}=\frac{1 \pm\left(1+4 a^{2}\right)}{2 a}=\left\{\begin{array}{l}{\dfrac{1+2 a^{2}}{a}}>1,\text{非解} \\ {-2 a},\quad \text{解}\end{array}\right.$$
因此有
$$\sin \phi=-2 a$$
故光线偏折角
$$\delta=4 a$$
$$a=\frac{G M}{c^{2} b}$$
$$\delta=\frac{4 G M}{c^{2} b}$$
研究光线紧靠太阳而过的偏折角,这时
$$b=R_{\odot},\quad \text{太阳半径}$$
$$M=M_{\odot},\quad \text{太阳质量}$$
则
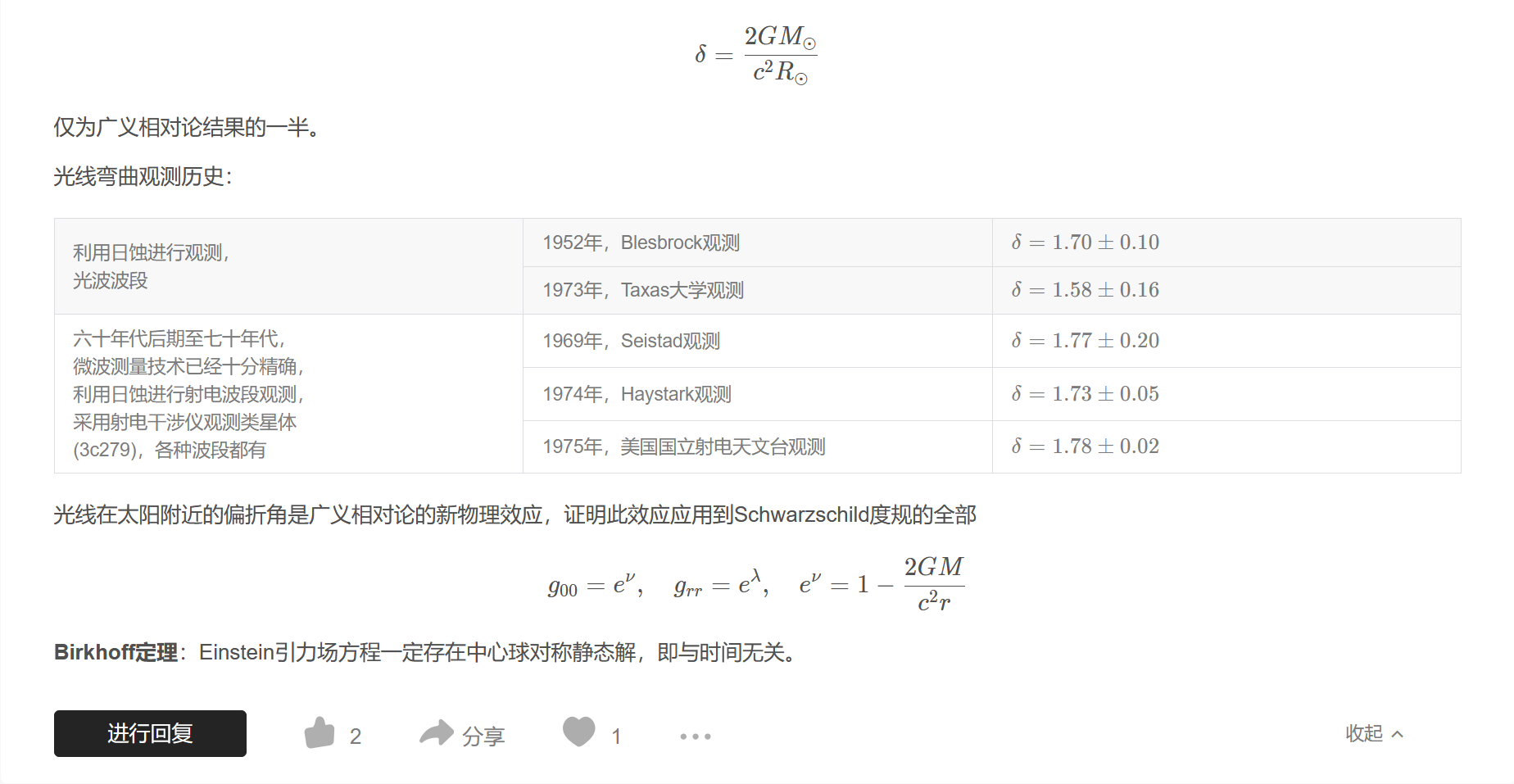
$$\delta=\frac{4 G M_{\odot}}{c^{2} R_{\odot}}$$
通常在日全蚀时观测靠近太阳的行星光线
$$\delta=1.75^{\prime\prime}$$
如用Newton力学计算,设光子的质量
$$m=\frac{h \nu}{c^{2}}$$
计算结果为
$$\delta=\frac{2 G M_{\odot}}{c^{2} R_{\odot}}$$
仅为广义相对论结果的一半。
光线弯曲观测历史:
| 利用日蚀进行观测, 光波波段 | 1952年,Blesbrock观测 | $\delta=1.70\pm 0.10$ |
| 1973年,Taxas大学观测 | $\delta=1.58\pm 0.16$ | |
| 六十年代后期至七十年代, 微波测量技术已经十分精确, 利用日蚀进行射电波段观测, 采用射电干涉仪观测类星体 (3c279),各种波段都有 | 1969年,Seistad观测 | $\delta=1.77\pm 0.20$ |
| 1974年,Haystark观测 | $\delta=1.73\pm 0.05$ | |
| 1975年,美国国立射电天文台观测 | $\delta=1.78\pm0.02$ |
光线在太阳附近的偏折角是广义相对论的新物理效应,证明此效应应用到Schwarzschild度规的全部
$$g_{00}=e^{\nu}, \quad g_{r r}=e^{\lambda}, \quad e^{\nu}=1-\frac{2 G M}{c^{2} r}$$
Birkhoff定理:Einstein引力场方程一定存在中心球对称静态解,即与时间无关。