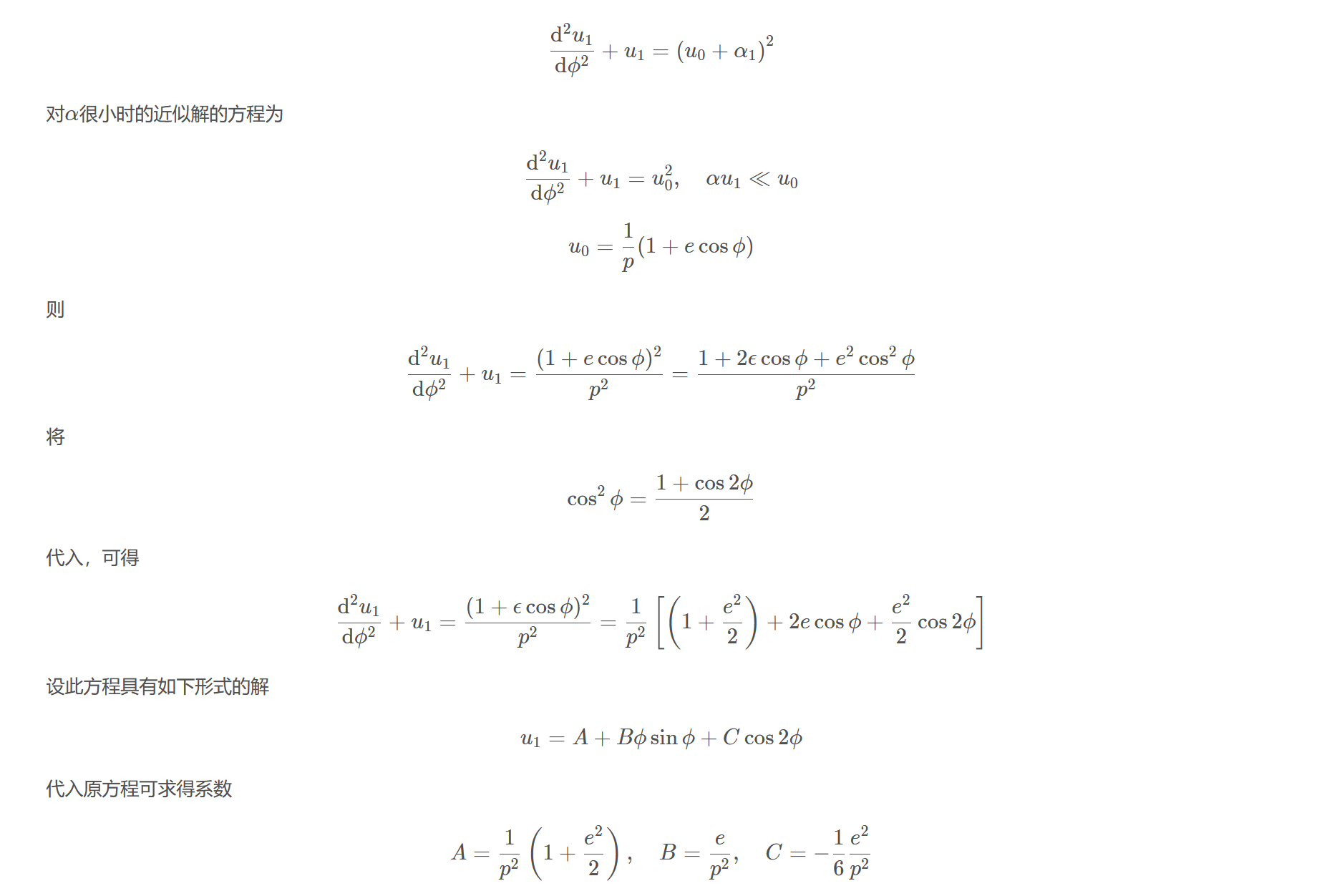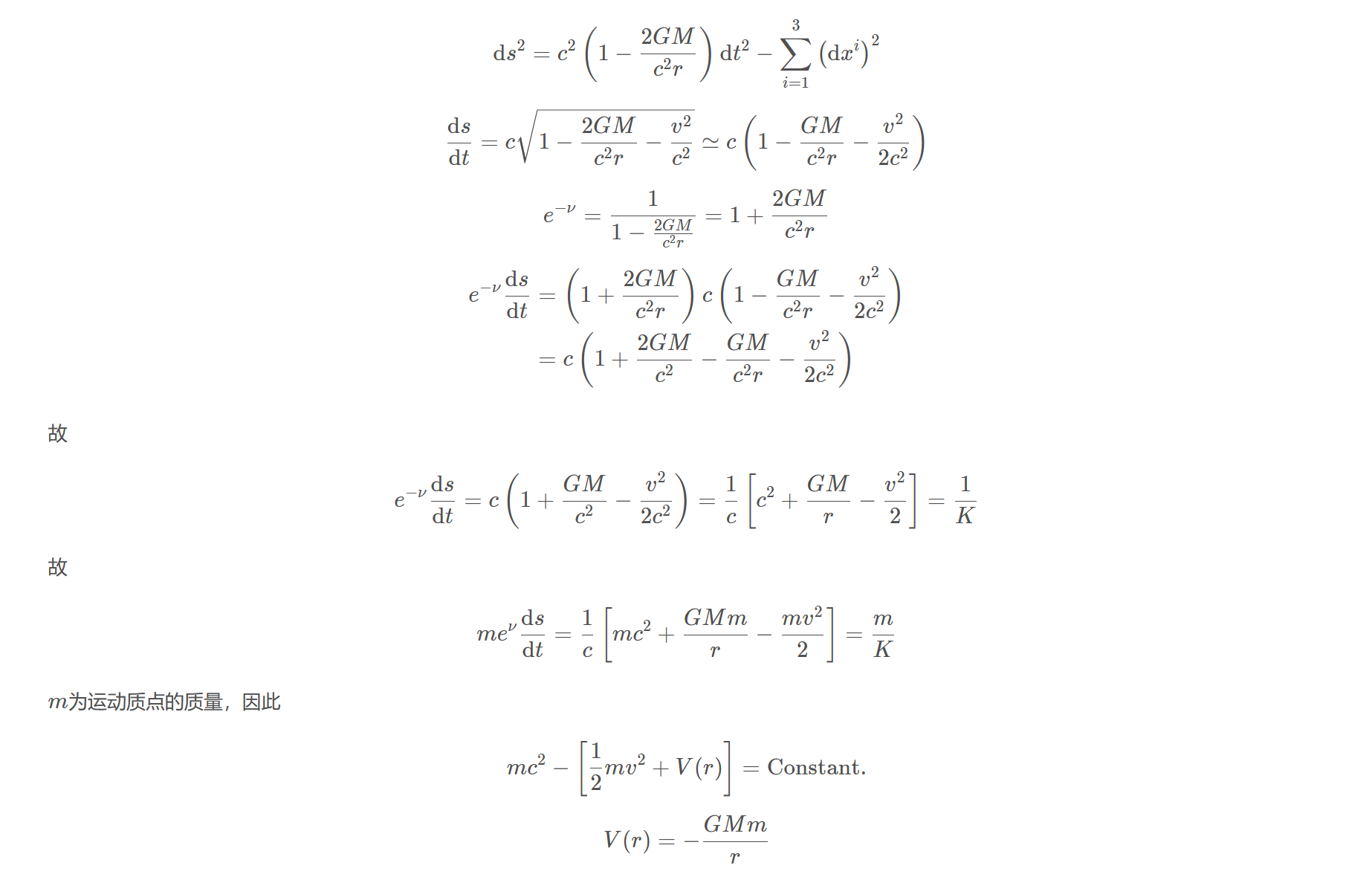物理 【广义相对论速成版】3. 中心球对称解与新引力效应 3.2 行星轨道进动 (B)
6. 广义行星运动方程(3.20)的解
设$u_{0}$满足Binet方程
$$\frac{\mathrm{d}^{2} u_{0}}{\mathrm{d} \phi^{2}}+u_{0}=\frac{G M}{h^{2}}$$
解为
$$u_{0}=\frac{1}{p}(1+e \cos \phi)$$
令
$$\alpha=\frac{3 G M}{c^{2}}, \quad \alpha\text{是一个小量}$$
则
$$\frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}+u=\alpha u^{2}+\frac{G M}{h^{2}}$$
设其解为
$$u=u_{0}+\alpha u_{1}$$
$$\frac{\mathrm{d}^{2} u_{0}}{\mathrm{d} \phi^{2}}+u_{0}+\alpha \frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+\alpha u_{1}=\alpha\left(u_{0}+\alpha u_{1}\right)^{2}+\frac{G M}{h^{2}}$$
由于$u_{0}$满足Binet方程,故$u_{1}$的方程为
$$\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}=\left(u_{0}+\alpha_{1}\right)^{2}$$
对$\alpha$很小时的近似解的方程为
$$\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}=u_{0}^{2}, \quad \alpha u_{1}\ll u_{0}$$
$$u_{0}=\frac{1}{p}(1+e \cos \phi)$$
则
$$\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}=\frac{(1+e \cos \phi)^{2}}{p^{2}}=\frac{1+2 \epsilon \cos \phi+e^{2} \cos ^{2} \phi}{p^{2}}$$
将
$$\cos ^{2} \phi=\frac{1+\cos 2 \phi}{2}$$
代入,可得
$$\frac{\mathrm{d}^{2} u_{1}}{\mathrm{d} \phi^{2}}+u_{1}=\frac{(1+\epsilon \cos \phi)^{2}}{p^{2}}=\frac{1}{p^{2}}\left[\left(1+\frac{e^{2}}{2}\right)+2 e \cos \phi+\frac{e^{2}}{2} \cos 2 \phi\right]$$
设此方程具有如下形式的解
$$u_{1}=A+B \phi \sin \phi+C \cos 2 \phi$$
代入原方程可求得系数
$$A=\frac{1}{p^{2}}\left(1+\frac{e^{2}}{2}\right), \quad B=\frac{e}{p^{2}}, \quad C=-\frac{1}{6} \frac{e^{2}}{p^{2}}$$
即
$$u_{1}=\frac{1}{p^{2}}\left(1+\frac{e^{2}}{2}\right)+\frac{e}{p^{2}} \phi \sin \phi-\frac{1}{6} \frac{e^{2}}{p^{2}} \cos 2 \phi$$
由
$$u=u_{0}+\alpha u_{1}$$
可得
$$u=\frac{1}{p}\left[(1+e\cos \phi)+\frac{\alpha}{p}\left(1+\frac{e^{2}}{2}\right)+\frac{\alpha e}{p} \phi \sin \phi-\frac{1}{6} \frac{\alpha e^{2}}{p} \cos 2 \phi\right]$$
上式中只有$\phi\sin\phi$是累积增加的,对轨道变迁有长期影响,而上式右端第二项和第四项无长期影响,仅对轨道形状有小的修正。故
$$u=\frac{1}{p}\left[(1+e \cos \phi)+\frac{\alpha e}{p} \phi \sin \phi\right]$$
因$\alpha$是一个小量,则$\frac{\alpha \phi}{p}$也是一个小量,则近似有
$$\cos \left(\phi-\frac{\alpha}{p} \phi\right)=\cos \phi \cos \frac{\alpha}{p} \phi+\sin \phi \sin \frac{\alpha}{p} \phi \simeq \cos \phi+\frac{\alpha}{p} \phi \sin \phi$$
故
$$u=\frac{1}{p}\left[\left(1+e \cos \phi\left(1-\frac{\alpha}{p}\right)\right]\right.$$
令
$$\Phi=\phi\left(1-\frac{\alpha}{p}\right)$$
则
$$r=\frac{p}{1+e \cos \Phi}$$
\subsection{行星轨道运动的进动}
当
$$\Phi_{n}=\phi_{n}\left(1-\frac{\alpha}{p}\right)=\left(2n+1\right)$$
$r$最大,这时
$$\cos\Phi=\cos\phi\left(1-\frac{\alpha}{p}\right)=-1$$
$$r=\frac{p}{1-e}$$
设
$$\phi_{n}=\left(2n+1\right)\pi\left(1-\frac{\alpha}{p}\right)^{-1}=\left(2n+1\right)\pi\left(1+\frac{\alpha}{p}\right)$$
$$\phi_{n+1}=\left(2n+3\right)\pi\left(1+\frac{\alpha}{p}\right)$$
故$\phi$的增量为
$$\phi_{n+1}-\phi{n}=2\pi\left(1+\frac{\alpha}{p}\right)=2\pi+2\pi\frac{\alpha}{p}$$
故$op$,也即轨道最远点。当$n\to n+1$,变化为
$$\Delta=2\pi\frac{2\pi}{p}=\frac{6\pi GM}{c^{2}p},\quad \frac{3 GM}{c^{2}}$$
即轨道进动角
$$\Delta=\frac{6\pi GM}{c^{2}p}$$
对应一周期的进动角。因
$$T^{2}=\frac{4\pi^{2}}{GM}a^{3},\quad GM=4\pi^{2}\frac{a^{3}}{T^{2}},\quad p=a\left(1-e^{2}\right)$$
则
$$\Delta=\frac{24\pi^{3}a^{2}}{c^{2}T^{2}\left(1-e^{2}\right)},\quad\text{一周期的进动角}$$
故$100$周的进动角为
$$\Delta_{c}=\frac{2400\pi^{3}a^{2}}{c^{2}T^{2}\left(1-e^{2}\right)}$$
一般都是以地球轨道长径为单位,行星周期$T$是以地球年为单位来计算。
地球轨道长径
$$a=1.4946\times 10^{11}m$$
$$1\text{年}=365.2564\text{天}$$
$$1\text{天}=24\times 60\times 60\text{秒}$$
则行星进动每世纪(Century)
$$\Delta_{c}=\frac{3.841a^{2}}{T^{3}\left(1-e^{2}\right)}\text{秒},\quad 100\text{年进动角}$$
水星的计算
$$\Delta_{c}=\frac{3.841a^{2}}{T^{3}\left(1-e^{2}\right)}=\frac{3.841\left(0.387\right)^{2}}{T\left(0.2408\right)^{3}\left(1-\left(0.2056\right)^{2}\right)}=43.0268^{\prime\prime}$$
即
$$\Delta_{c}=43.03^{\prime\prime}$$
$1956$年水星观测值是
$$\begin{aligned}43.11\pm 0.45^{\prime\prime}\\42.56\pm 0.94^{\prime\prime}\end{aligned}$$
水星进动较大,每百年$\Delta_{c}$
| 参数 | 地球 | 水星 | 金星 | 火星 |
|---|---|---|---|---|
| a | 1.000 | 0.387 | 0.732 | 1.524 |
| T(年) | 1.0000 | 0.2408 | 0.6152 | 1.8881 |
| e | 0.0170 | 0.2056 | 0.0070 | 0.0930 |
| Δc | 3.84″ | 43.03″ | 8.63″ | 1.34″ |
$$\Delta_{c}=43.03^{\prime\prime}$$
天文观测已精确证实。它是广义相对论预言的新引力效应,并为天文观测所证实。
8. 广义行星运动方程的物理意义
方程(3.12)
$$\frac{\mathrm{d}^{2}t}{\mathrm{d}s^{2}}+\nu^{\prime}\frac{\mathrm{d}r}{\mathrm{d}s}\frac{\mathrm{d}t}{\mathrm{d}s}=0$$
即
$$\frac{\mathrm{d}^{2}t}{\mathrm{d}s^{2}}+\frac{\mathrm{d}\nu}{\mathrm{d}r}\frac{\mathrm{d}r}{\mathrm{d}s}\frac{\mathrm{d}t}{\mathrm{d}s}=0$$
$$\frac{\mathrm{d}^{2}t}{\mathrm{d}s^{2}}+\frac{\mathrm{d}\nu}{\mathrm{d}s}\frac{\mathrm{d}t}{\mathrm{d}s}=0$$
$$\frac{\frac{\mathrm{d}}{\mathrm{d}s}\left(\frac{\mathrm{d}t}{\mathrm{d}s}\right)}{\frac{\mathrm{d}t}{\mathrm{d}s}}=-\frac{\mathrm{d}\nu}{\mathrm{d}s}$$
$$\mathrm{d}\left(\ln\left(\frac{\mathrm{d}t}{\mathrm{d}s}\right)\right)=-\mathrm{d}\left(\ln e^{\nu}\right)$$
其解为
$$\ln\left(\frac{\mathrm{d}t}{\mathrm{d}s}\right)=-\ln e^{\nu}+\ln K$$
即
$$e^{\nu}\frac{\mathrm{d}t}{\mathrm{d}s}=K$$
也即
$$e^{-\nu}\frac{\mathrm{d}s}{\mathrm{d}t}=\frac{1}{K}$$
我们知道在Newton近似下
$$\mathrm{d}s^{2}=c^{2}\left(1-\frac{2GM}{c^{2}r}\right)\mathrm{d}t^{2}-\sum_{i=1}^{3}\left(\mathrm{d}x^{i}\right)^{2}$$
$$\frac{\mathrm{d}s}{\mathrm{d}t}=c\sqrt{1-\frac{2GM}{c^{2}r}-\frac{v^{2}}{c^{2}}}\simeq c\left(1-\frac{GM}{c^{2}r}-\frac{v^{2}}{2c^{2}}\right)$$
$$e^{-\nu}=\frac{1}{1-\frac{2GM}{c^{2}r}}=1+\frac{2GM}{c^{2}r}$$
$$\begin{aligned}e^{-\nu}\frac{\mathrm{d}s}{\mathrm{d}t}&=\left(1+\frac{2GM}{c^{2}r}\right)c\left(1-\frac{GM}{c^{2}r}-\frac{v^{2}}{2c^{2}}\right)\\&=c\left(1+\frac{2GM}{c^{2}}-\frac{GM}{c^{2}r}-\frac{v^{2}}{2c^{2}}\right)\end{aligned}$$
故
$$e^{-\nu}\frac{\mathrm{d}s}{\mathrm{d}t}=c\left(1+\frac{GM}{c^{2}}-\frac{v^{2}}{2c^{2}}\right)=\frac{1}{c}\left[c^{2}+\frac{GM}{r}-\frac{v^{2}}{2}\right]=\frac{1}{K}$$
故
$$m e^{\nu}\frac{\mathrm{d}s}{\mathrm{d}t}=\frac{1}{c}\left[mc^{2}+\frac{GMm}{r}-\frac{mv^{2}}{2}\right]=\frac{m}{K}$$
$m$为运动质点的质量,因此
$$mc^{2}-\left[\frac{1}{2}mv^{2}+V(r)\right]=\text{Constant.}$$
$$V(r)=-\frac{GMm}{r}$$
$$\frac{1}{2}mv^{2}+V(r)=\text{Constant.}$$
相当于能量守恒(若不乘以$m$,则是单位质点的能量守恒。)
概括而言
$$e^{\nu}\frac{\mathrm{d}t}{\mathrm{d}s}=K$$
代表广义相对论中行星运动的新守恒量,也即新的能量守恒定律。