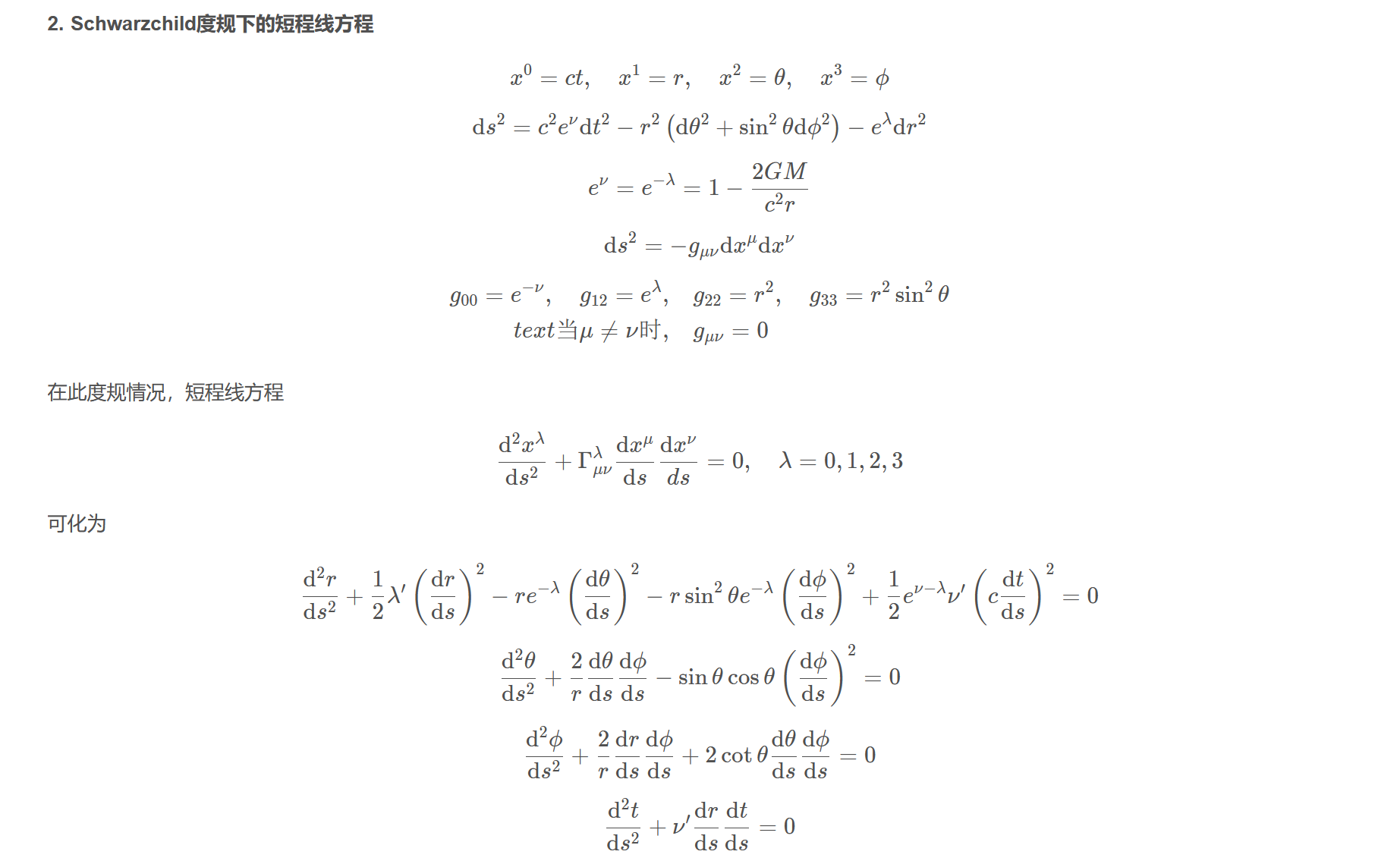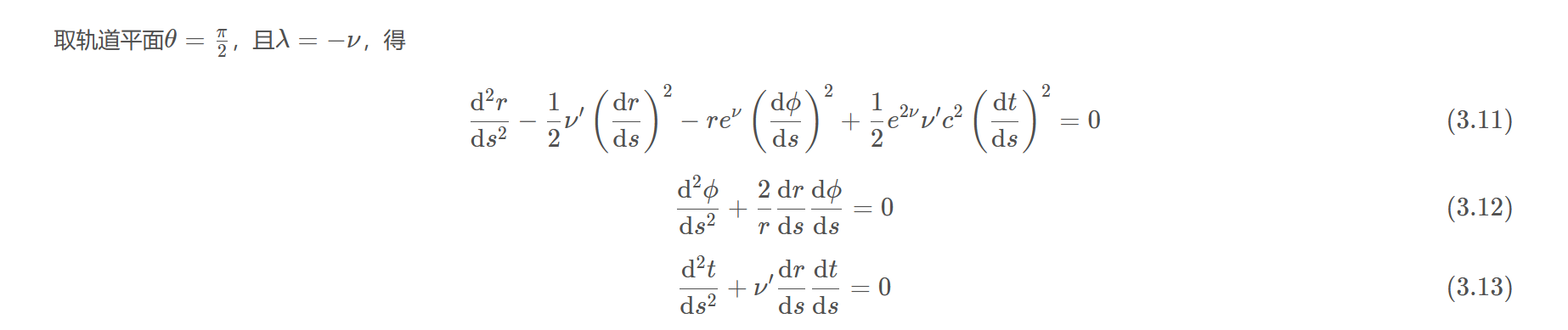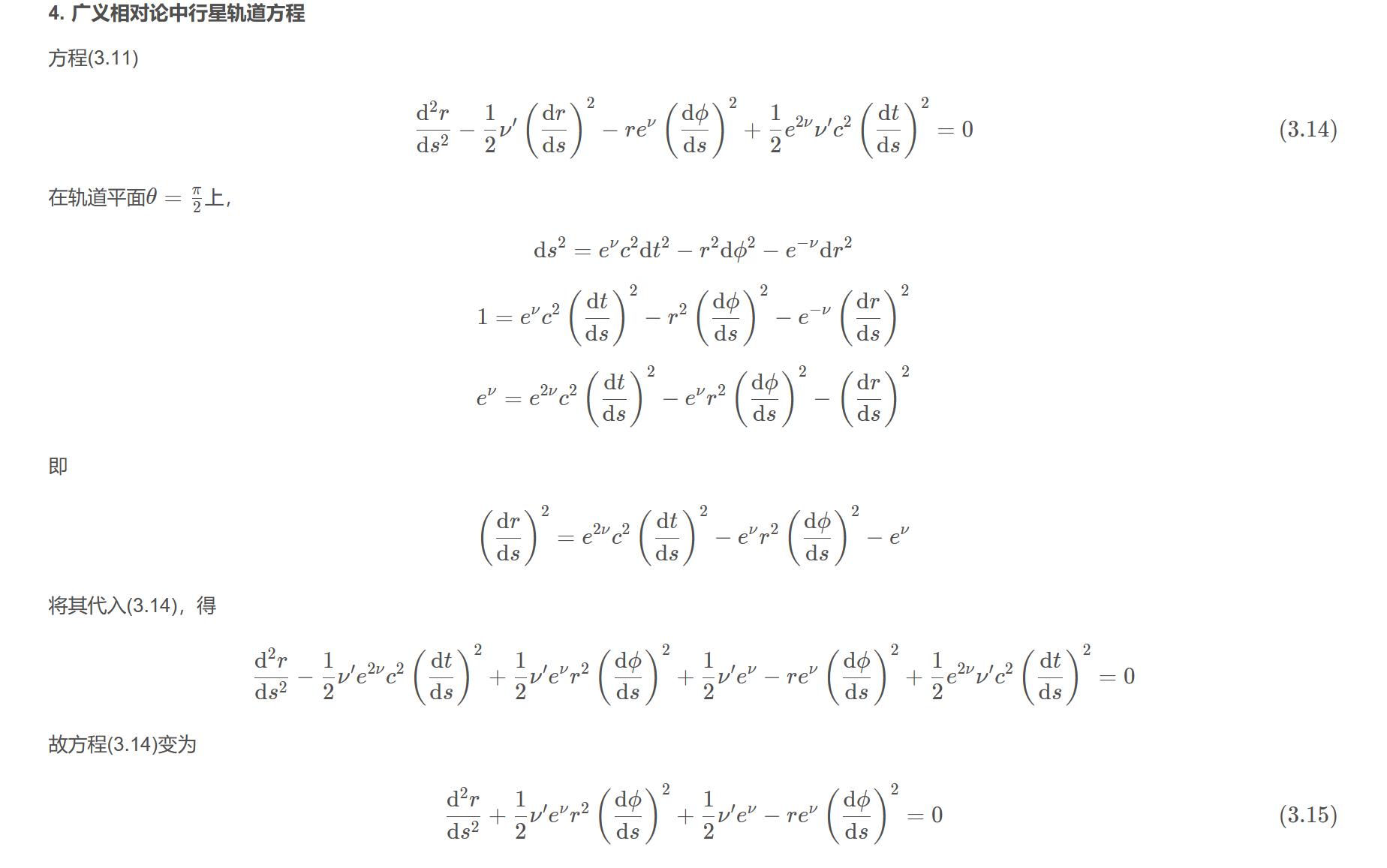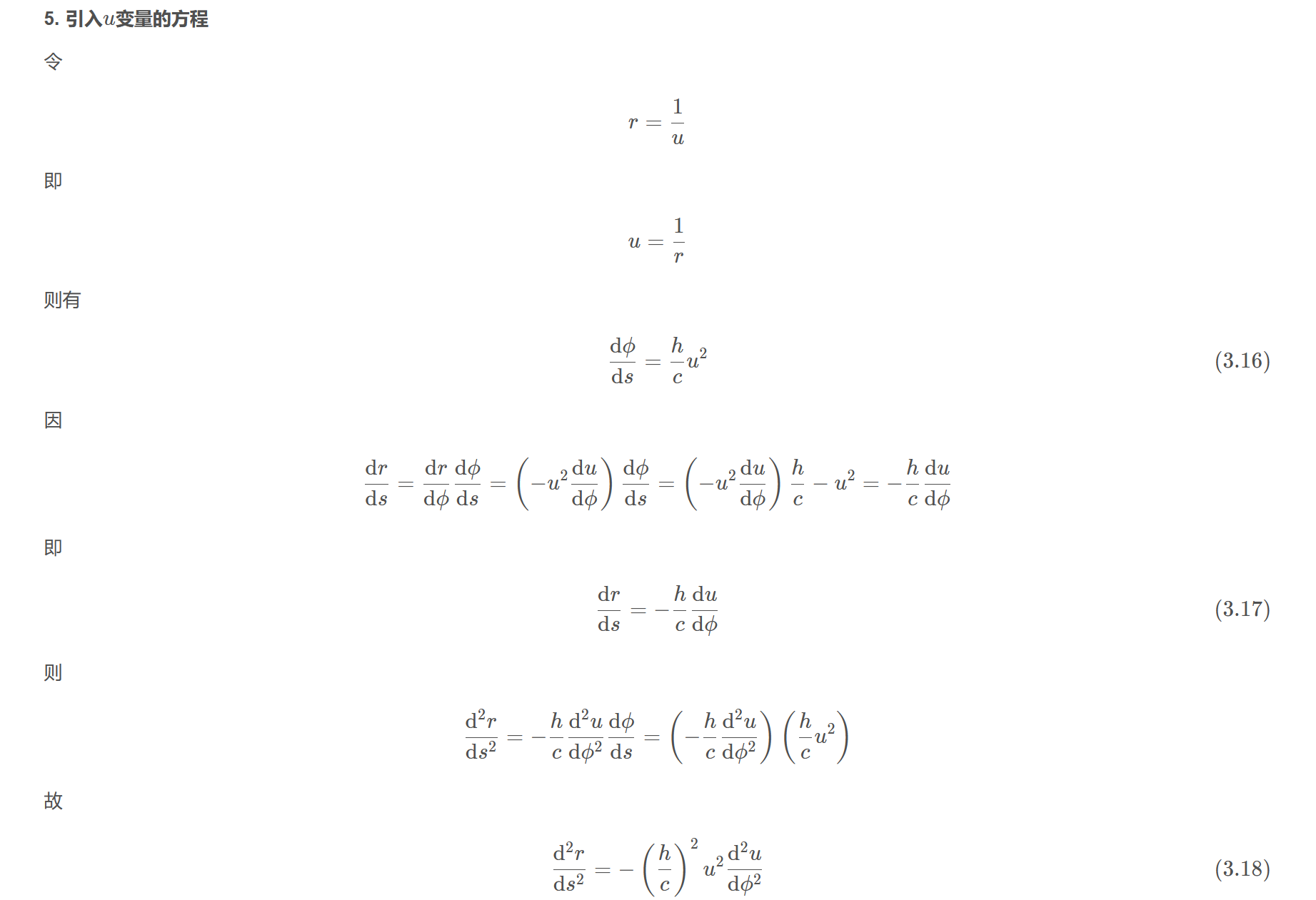【广义相对论速成版】3. 中心球对称解与新引力效应 3.2 行星轨道进动 (A)

1. Newton力学和万有引力作用下的行星进动

$$\frac{\mathrm{d}^{2} \vec{r}}{\mathrm{d} t^{2}}=-\frac{G M}{r^{3}} \vec{r}$$

轨道面为

$$\theta=\frac{\pi}{2}$$

(1) 面速不变

$$r^{2} \frac{\mathrm{d} \phi}{\mathrm{d} t}=h$$

也即

$$\frac{\mathrm{d} A}{\mathrm{d} t}=\frac{1}{2} r^{2} \frac{\mathrm{d} \phi}{\mathrm{d} t}=\frac{1}{2} h$$

面积速度为常数。

(2) Binet方程

设

$$u=\frac{1}{r}$$

Binet推导出

$$\frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}+u=\frac{G M}{h^{2}},\quad \text{Binet方程}$$

(3) 轨道方程(由Binet方程可推出来)

$$u=\frac{1}{p}(1+e \cos \phi)$$

或

$$r=\frac{p}{1+e \cos \phi}, \quad \quad p=\frac{h^{2}}{G M}$$

当$e<1$，是椭圆，长径

$$a=\frac{p}{1-e^{2}}$$

短径

$$b^{2}=\frac{p^{2}}{1-\epsilon^{2}}$$

$$p=\frac{b^{2}}{a}$$

(4) 周期

$$T=\frac{2 \pi}{\sqrt{G M}} a^{\frac{3}{2}}$$

2. Schwarzchild度规下的短程线方程

$$x^{0}=ct,\quad x^{1}=r,\quad x^{2}=\theta,\quad x^{3}=\phi$$

$$\mathrm{d} s^{2}=c^{2} e^{\nu} \mathrm{d} t^{2}-r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)-e^{\lambda} \mathrm{d} r^{2}$$

$$e^{\nu}=e^{-\lambda}=1-\frac{2 G M}{c^{2} r}$$

$$\mathrm{d} s^{2}=-g_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}$$

$$\begin{aligned}g_{00}=e^{-\nu}, \quad g_{12}=e^{\lambda},& \quad g_{22}=r^{2}, \quad g_{33}=r^{2} \sin ^{2} \theta\\text{当}\mu\neq\nu\text{时},& \quad g_{\mu \nu}=0\end{aligned}$$

在此度规情况，短程线方程

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} s^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} s} \frac{\mathrm{d} x^{\nu}}{d s}=0, \quad \lambda=0,1,2,3$$

可化为

$$\frac{\mathrm{d}^{2} r}{\mathrm{d} s^{2}}+\frac{1}{2} \lambda^{\prime}\left(\frac{\mathrm{d} r}{\mathrm{d} s}\right)^{2}-r e^{-\lambda}\left(\frac{\mathrm{d} \theta}{\mathrm{d} s}\right)^{2}-r \sin ^{2} \theta e^{-\lambda}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}+\frac{1}{2} e^{\nu-\lambda} \nu^{\prime}\left(c \frac{\mathrm{d} t}{\mathrm{d} s}\right)^{2}=0$$

$$\frac{\mathrm{d}^{2} \theta}{\mathrm{d} s^{2}} + \frac{2}{r} \frac{\mathrm{d} \theta}{\mathrm{d} s} \frac{\mathrm{d} \phi}{\mathrm{d} s}-\sin \theta \cos \theta\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}=0$$

$$\frac{\mathrm{d}^{2} \phi}{\mathrm{d} s^{2}}+\frac{2}{r} \frac{\mathrm{d} r}{\mathrm{d} s} \frac{\mathrm{d} \phi}{\mathrm{d} s}+2 \cot \theta \frac{\mathrm{d} \theta}{\mathrm{d} s} \frac{\mathrm{d} \phi}{\mathrm{d} s}=0$$

$$\frac{\mathrm{d}^{2} t}{\mathrm{d} s^{2}}+\nu^{\prime} \frac{\mathrm{d} r}{\mathrm{d} s} \frac{\mathrm{d} t}{\mathrm{d} s}=0$$

取轨道平面$\theta=\frac{\pi}{2}$，且$\lambda=-\nu$，得

$$\frac{\mathrm{d}^{2} r}{\mathrm{d} s^{2}}-\frac{1}{2} \nu^{\prime}\left(\frac{\mathrm{d} r}{\mathrm{d} s}\right)^{2}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}+\frac{1}{2} e^{2 \nu} \nu^{\prime} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} s}\right)^{2}=0\tag{3.11}$$

$$\frac{\mathrm{d}^{2} \phi}{\mathrm{d} s^{2}}+\frac{2}{r} \frac{\mathrm{d} r}{\mathrm{d} s} \frac{\mathrm{d} \phi}{\mathrm{d} s}=0\tag{3.12}$$

$$\frac{\mathrm{d}^{2} t}{\mathrm{d} s^{2}}+\nu^{\prime} \frac{\mathrm{d} r}{\mathrm{d} s} \frac{\mathrm{d} t}{\mathrm{d} s}=0\tag{3.13}$$

3. 面积速度不变

由方程(3.12)

$$r^{2} \frac{\mathrm{d}^{2} \phi}{\mathrm{d} s^{2}}+2 r \frac{\mathrm{d} r}{\mathrm{d} s} \frac{\mathrm{d} \phi}{\mathrm{d} s}=0$$

知

$$r^{2} \frac{\mathrm{d}^{2} \phi}{\mathrm{d} s^{2}}+\frac{\mathrm{d} r^{2}}{\mathrm{d} s} \frac{\mathrm{d} \phi}{\mathrm{d} s}=0$$

$$\frac{\mathrm{d}}{\mathrm{d} s}\left(r^{2} \frac{\mathrm{d} \phi}{\mathrm{d} s}\right)=0$$

令

$$\mathrm{d} s=c \mathrm{d} \tau,\quad \text{以后将知道}\tau\text{称为固有时}$$

则

$$r^{2} \frac{\mathrm{d} \phi}{\mathrm{d} \tau}=\text{Constant.}$$

令

$$r^{2} \frac{\mathrm{d} \phi}{\mathrm{d} \tau}=h$$

$$\mathrm{d} A=\frac{1}{2} r^{2} \mathrm{d} \phi$$

故

$$\frac{\mathrm{d} A}{\mathrm{d} \tau}=\frac{1}{2} r^{2} \frac{\mathrm{d} \phi}{\mathrm{d} \tau}=\frac{1}{2} h$$

即面积速度不变。

短程线方程

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} s^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} s} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} s}=0$$

与Newton力学的差别为$\mathrm{d} s$不是时间，$\mathrm{d} s$的量纲不是时间$T$而是$L$，但是将$\mathrm{d} s$写成

$$\mathrm{d} s=c \mathrm{d}\tau$$

则$\mathrm{d}\tau$具有时间的量纲$T$，$\tau$称为固有时。则短程线方程可写成

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} \tau^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} \tau} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} \tau}=0$$

运动轨迹为$\tau$的函数

$$x^{\mu}=x^{\mu}(\tau)$$

即$\tau$为描述粒子运动真正的时间。上述面积速度不变是对固有时不变的。

4. 广义相对论中行星轨道方程

方程(3.11)

在轨道平面$\theta=\frac{\pi}{2}$上，

$$\mathrm{d} s^{2}=e^{\nu} c^{2} \mathrm{d} t^{2}-r^{2} \mathrm{d} \phi^{2}-e^{-\nu} \mathrm{d} r^{2}$$

$$1=e^{\nu} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} s}\right)^{2}-r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}-e^{-\nu}\left(\frac{\mathrm{d} r}{\mathrm{d} s}\right)^{2}$$

$$e^{\nu}=e^{2 \nu} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} s}\right)^{2}-e^{\nu} r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}-\left(\frac{\mathrm{d} r}{\mathrm{d} s}\right)^{2}$$

即

$$\left(\frac{\mathrm{d} r}{\mathrm{d} s}\right)^{2}=e^{2 \nu} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} s}\right)^{2}-e^{\nu} r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}-e^{\nu}$$

将其代入(3.14)，得

$$\frac{\mathrm{d}^{2} r}{\mathrm{d} s^{2}}-\frac{1}{2} \nu^{\prime} e^{2 \nu} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} s}\right)^{2}+\frac{1}{2} \nu^{\prime} e^{\nu} r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}+\frac{1}{2} \nu^{\prime} e^{\nu}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}+\frac{1}{2} e^{2 \nu} \nu^{\prime} c^{2}\left(\frac{\mathrm{d} t}{\mathrm{d} s}\right)^{2}=0$$

故方程(3.14)变为

$$\frac{\mathrm{d}^{2} r}{\mathrm{d} s^{2}}+\frac{1}{2} \nu^{\prime} e^{\nu} r^{2}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}+\frac{1}{2} \nu^{\prime} e^{\nu}-r e^{\nu}\left(\frac{\mathrm{d} \phi}{\mathrm{d} s}\right)^{2}=0\tag{3.15}$$

5. 引入$u$变量的方程

令

$$r=\frac{1}{u}$$

即

$$u=\frac{1}{r}$$

则有

$$\frac{\mathrm{d} \phi}{\mathrm{d} s}=\frac{h}{c} u^{2}\tag{3.16}$$

因

$$\frac{\mathrm{d} r}{\mathrm{d} s}=\frac{\mathrm{d} r}{\mathrm{d} \phi} \frac{\mathrm{d} \phi}{\mathrm{d} s}=\left(-u^{2} \frac{\mathrm{d} u}{\mathrm{d} \phi}\right) \frac{\mathrm{d} \phi}{\mathrm{d} s}=\left(-u^{2} \frac{\mathrm{d} u}{\mathrm{d} \phi}\right)\frac{h}{c}-u^{2}=-\frac{h}{c} \frac{\mathrm{d} u}{\mathrm{d} \phi}$$

即

$$\frac{\mathrm{d} r}{\mathrm{d} s}=-\frac{h}{c} \frac{\mathrm{d} u}{\mathrm{d} \phi}\tag{3.17}$$

则

$$\frac{\mathrm{d}^{2} r}{\mathrm{d} s^{2}}=-\frac{h}{c} \frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}} \frac{\mathrm{d} \phi}{\mathrm{d} s}=\left(-\frac{h}{c} \frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}\right)\left(\frac{h}{c} u^{2}\right)$$

故

$$\frac{\mathrm{d}^{2} r}{\mathrm{d} s^{2}}=-\left(\frac{h}{c}\right)^{2} u^{2} \frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}\tag{3.18}$$

此外由于

$$e^{\nu}=1-\frac{2 G M}{c^{2} r}=1-\frac{2 G M}{c^{2}} u$$

$$\left(e^{\nu}\right)^{\prime}=\frac{1}{r^{2}} \cdot \frac{2 G M}{c^{2}}=\frac{2 G M}{c^{2}} u^{2}$$

又

$$\left(e^{\nu}\right)^{\prime}=e^{\nu} \nu^{\prime}$$

故

$$\nu^{\prime} e^{\nu}=\frac{2 G M}{c^{2}} u^{2}\tag{3.19}$$

将(3.16)、(3.17)、(3.18)、(3.19)代入(3.15)，可得

$$\frac{\mathrm{d}^{2} u}{\mathrm{d} \phi^{2}}+u=\frac{3 G M}{c^{2}} u^{2}+\frac{G M}{h^{2}}\tag{3.20}$$

此式可称为广义相对论中的Binet方程。

物理 【广义相对论速成版】3. 中心球对称解与新引力效应 3.2 行星轨道进动 (A)

物理
【广义相对论速成版】3. 中心球对称解与新引力效应 3.2 行星轨道进动 (A)