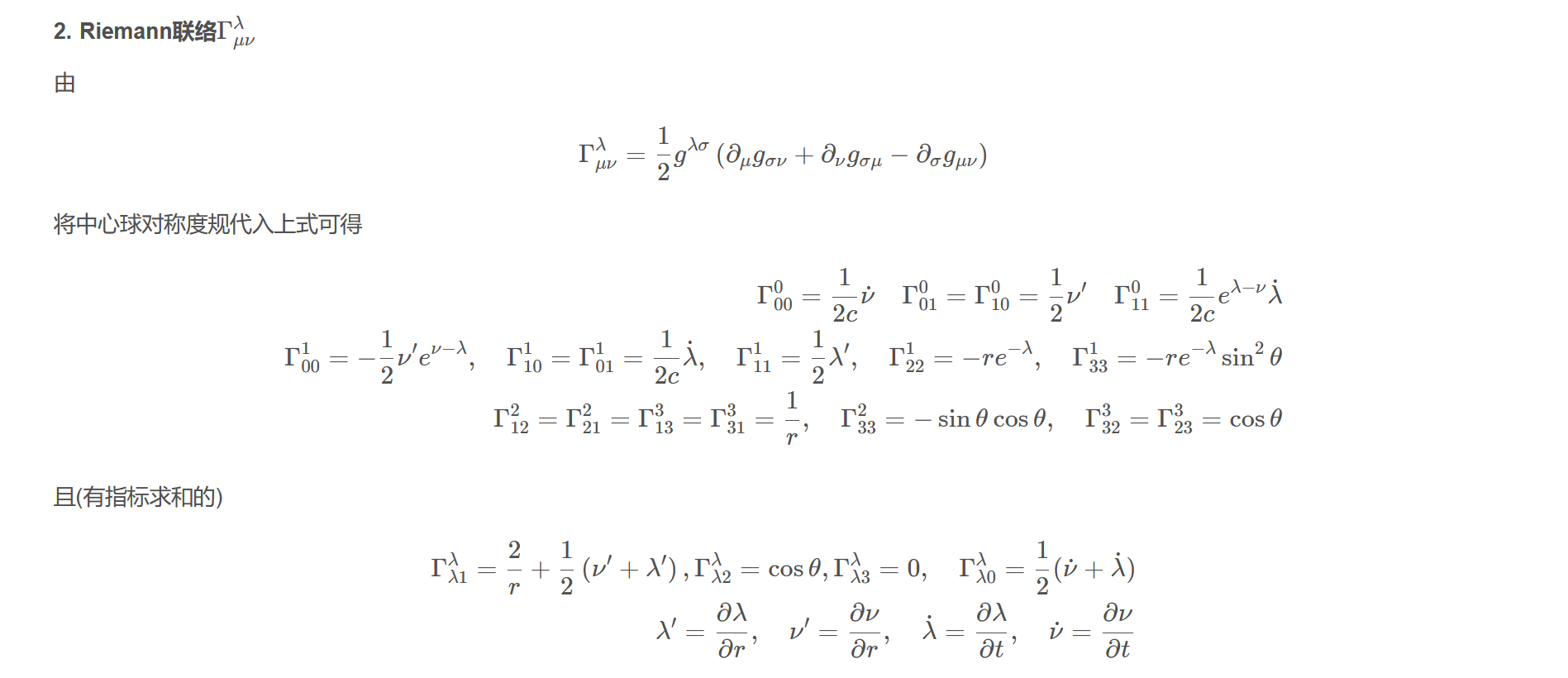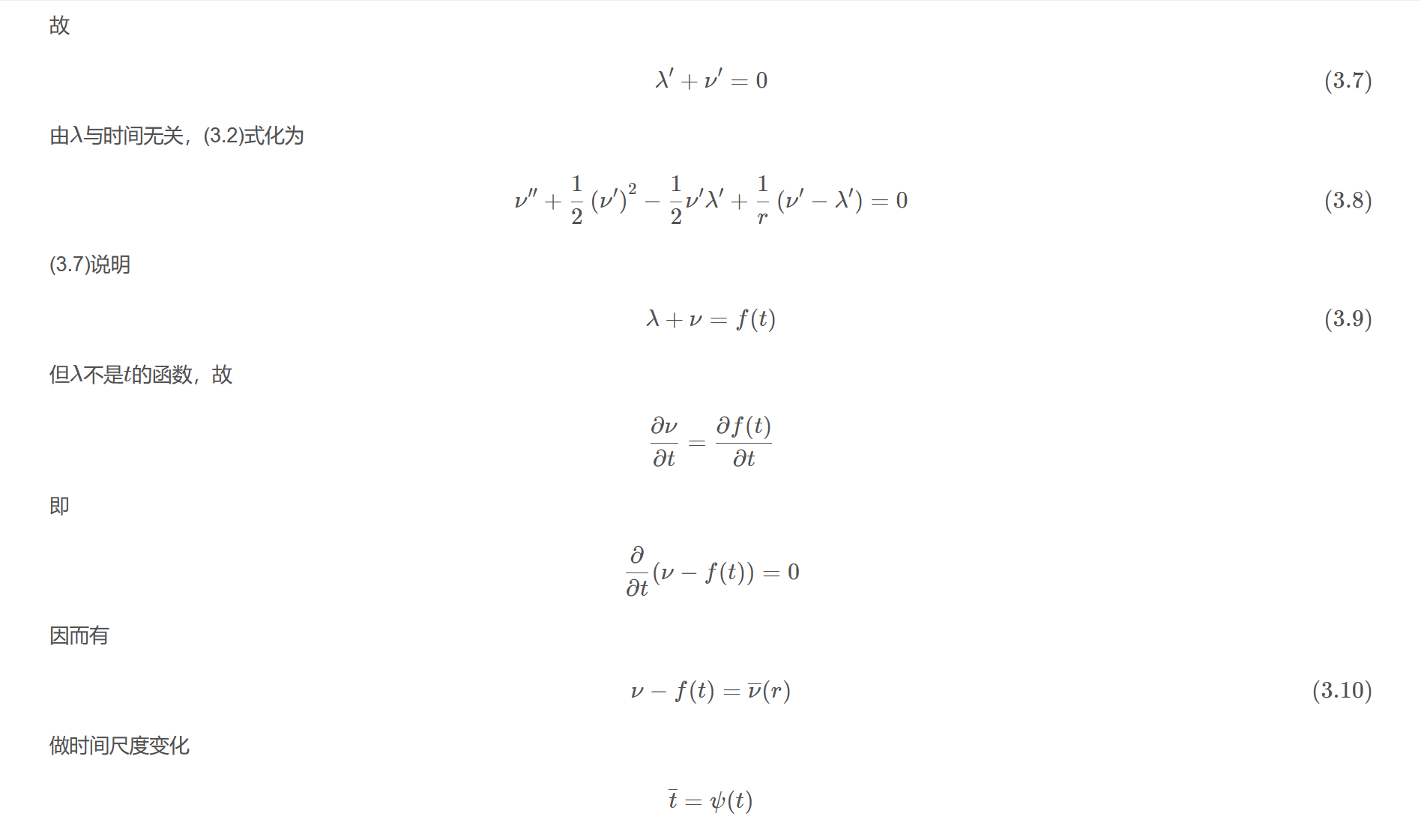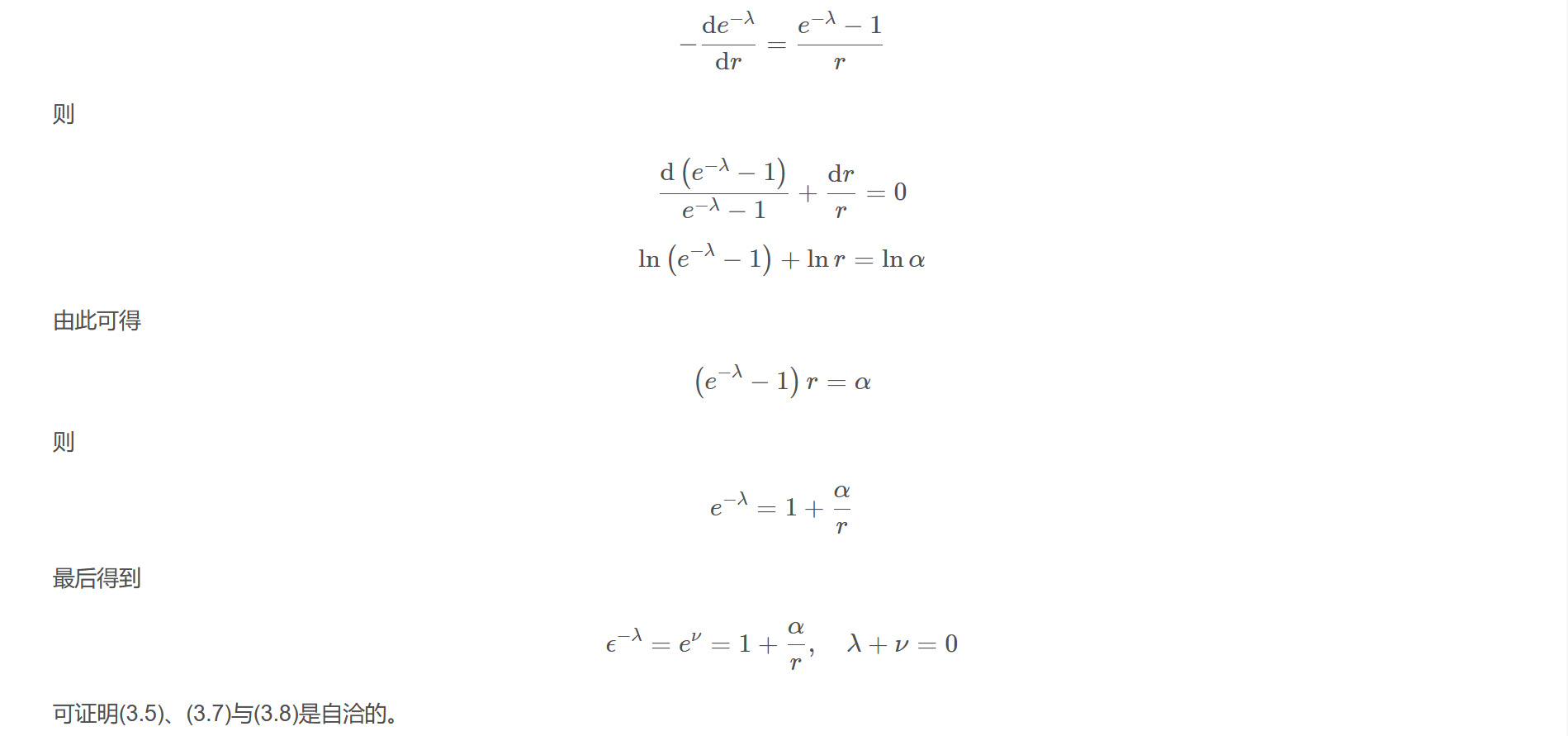物理

【广义相对论速成版】3. 中心球对称解与新引力效应 3.1 引力场的中心球对称解

宇宙大多数星体的质量分布都是中心球对称的，它将产生中心球对称引力场，即度规是中心球对称的。

1. 中心球对称的度规与弧元

半径为$R=a$的球面上的弧元$\mathrm{d}s^{2}$对$S^{2}$球坐标可表示为

$$\mathrm{d}s^{2}=r^{2}\left(\mathrm{d}\theta^{2}+\sin^{2}\theta\mathrm{d}\phi^{2}\right),\qquad r=a$$

$r^{2}$因子保证了$\mathrm{d}s$具有长度的量纲。三维Euclidean空间在球坐标

$$x^{1}=r, \quad x^{2}=\theta, \quad x^{3}=\phi$$

当$\mathrm{d}r=0$时，$\mathrm{d}s$为球面上的弧元，且在$r$相同的地方$\mathrm{d}s$具有相同的形式，这种表示称为中心球对称弧元。

四维赝欧时空，在$x^{0}=c t, x^{1}=r, x^{2}=\theta, x^{3}=\phi$的赝欧球坐标中，弧元

$$\mathrm{d} s^{2}=c^{2} \mathrm{d} t^{2}-\left[\mathrm{d} r^{2}+r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)\right]$$

它是四维平直时空的弧元(仅是后面用球坐标表示而已)，它的特征是弧元的空间部分

$$\mathrm{d} \ell^{2}=\mathrm{d} r^{2}+r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right),\quad \text{为中心球对称的弧元}$$

当$\mathrm{d}t=0,\mathrm{d}r=0$时

$$-\mathrm{d} s^{2}=r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)$$

为球面元。上述$\mathrm{d}s^{2}$的表述称为\textbf{四维赝欧时空的中心球对称表示}。$\mathrm{d}s^{2}$对所有$r$相同处具有相同的形式。

中心球对称Riemann时空要求弧元$\mathrm{d}s^{2}$对中心向径$r$相等的点具有相同的形式，并且在$\mathrm{d}t=0,\mathrm{d}r=0$时$-\mathrm{d}s^{2}$是球面弧元。一般还要求在无穷远处$\mathrm{d}s^{2}$变成赝欧时空中心球对称弧元

$$\mathrm{d} s^{2}=c^{2} \mathrm{d} t^{2}-\left[\mathrm{d} r^{2}+r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)\right]$$

对四维Riemann时空中的弧元$\mathrm{d}s^{2}$的中心球对称的一般形式可表示为

$$\mathrm{d} s^{2}=A \mathrm{d} r^{2}+B r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)+C \mathrm{d} r \mathrm{d} t+\mathrm{d} \mathrm{d} t^{2}$$

$A,B,C,D$仅为$r$和$t$的函数，它是保持中心球对称定义的弧元，此弧元仅允许下列两种变换

$$r^{\prime}=\overline{r}(r, t), \quad t^{\prime}=\overline{t}(r, t)$$

可以通过上述两个变换使

$$B=-1, \quad C=0$$

则

$$\mathrm{d} s^{2}=A \mathrm{d} r^{2}-r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)+D \mathrm{d} t^{2}$$

令

$$D=c^{2} e^{\nu}$$

当然$\nu$是$r$和$t$的函数，同时令

$$A=-e^{\lambda}$$

即

$$\mathrm{d} s^{2}=c^{2} e^{\nu} \mathrm{d} t^{2}-r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)-e^{\lambda} \mathrm{d} r^{2}$$

当$r\to\infty$时，$\nu=\lambda=0$，$\mathrm{d}s^{2}$可变成平直时空中心球对称弧元

$$\mathrm{d} s^{2}=c^{2} \mathrm{d} t^{2}-\left[\mathrm{d} r^{2}+r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)\right]$$

对坐标

$$x^{0}=c t, \quad x^{1}=r, \quad x^{2}=\theta, \quad x^{3}=\phi$$

对度规$g_{\mu\nu}$

$$\mathrm{d} s^{2}=-g_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}$$

$$\begin{aligned}g_{00}=-e^{\nu}, \quad g_{11}=e^{\lambda},& \quad g_{22}=r^{2}, \quad g_{33}=r^{2} \sin ^{2} \theta\\\text{当}\mu\neq\nu\text{时},&\quad g_{\mu\nu}=0 \end{aligned}$$

并且

$$g=-r^{4} \sin ^{2} \theta e^{\nu+\lambda}$$

$$\sqrt{-g}=r^{2} \sin \theta e^{\frac{v+\lambda}{2}}$$

2. Riemann联络$\Gamma_{\mu\nu}^{\lambda}$

由

$$\Gamma_{\mu \nu}^{\lambda}=\frac{1}{2} g^{\lambda \sigma}\left(\partial_{\mu} g_{\sigma \nu}+\partial_{\nu} g_{\sigma \mu}-\partial_{\sigma} g_{\mu \nu}\right)$$

将中心球对称度规代入上式可得

$$\begin{aligned}\Gamma_{00}^{0}=\frac{1}{2 c} \dot{\nu}\quad \Gamma_{01}^{0}=\Gamma_{10}^{0}=\frac{1}{2} \nu^{\prime}\quad \Gamma_{11}^{0}=\frac{1}{2 c} e^{\lambda-\nu} \dot{\lambda}\\\Gamma_{00}^{1}=-\frac{1}{2}\nu^{\prime}e^{\nu-\lambda},\quad \Gamma_{10}^{1}=\Gamma_{01}^{1}=\frac{1}{2 c} \dot{\lambda},\quad \Gamma_{11}^{1}=\frac{1}{2} \lambda^{\prime},\quad \Gamma_{22}^{1}=-r e^{-\lambda}, \quad \Gamma_{33}^{1}=-r e^{-\lambda} \sin ^{2} \theta\\\Gamma_{12}^{2}=\Gamma_{21}^{2}=\Gamma_{13}^{3}=\Gamma_{31}^{3}=\frac{1}{r}, \quad \Gamma_{33}^{2}=-\sin \theta \cos \theta,\quad \Gamma_{32}^{3}=\Gamma_{23}^{3}=\cos \theta\end{aligned}$$

且(有指标求和的)

$$\begin{aligned}\Gamma_{\lambda 1}^{\lambda}=\frac{2}{r}+\frac{1}{2}\left(\nu^{\prime}+\lambda^{\prime}\right), \Gamma_{\lambda 2}^{\lambda}=\cos \theta, \Gamma_{\lambda 3}^{\lambda}=0, \quad \Gamma_{\lambda 0}^{\lambda}=\frac{1}{2}(\dot{\nu}+\dot{\lambda})\\\lambda^{\prime}=\frac{\partial \lambda}{\partial r}, \quad \nu^{\prime}=\frac{\partial \nu}{\partial r}, \quad \dot{\lambda}=\frac{\partial \lambda}{\partial t}, \quad \dot{\nu}=\frac{\partial \nu}{\partial t}\end{aligned}$$

3. Einstein张量

由中心球对称情况的$\Gamma_{\mu\nu}^{\lambda}$可计算Einstein张量

$$G_{\nu}^{\mu}=R_{\nu}^{\mu}-\frac{1}{2} \delta_{\nu}^{\mu} R$$

$$\begin{aligned}R_{0}^{0}-\frac{1}{2} R&=e^{-\lambda}\left[\frac{1}{r^{2}}-\frac{1}{r} \lambda^{\prime}\right]-\frac{1}{r^{2}}\\R_{1}^{1}-\frac{1}{2} R&=e^{-\lambda}\left(\frac{1}{r} \nu^{\prime}+\frac{1}{r^{2}}\right)-\frac{1}{r^{2}}\\R_{2}^{2}-\frac{1}{2} R&=R_{3}^{3}-\frac{1}{2} R\\&=\frac{1}{2} e^{-\lambda}\left[\nu^{\prime \prime}+\frac{1}{2}\left(\nu^{\prime}\right)^{2}-\frac{1}{2} \nu^{\prime} \lambda^{\prime}+\frac{1}{r}\left(\nu^{\prime}-\lambda^{\prime}\right)\right]+\frac{1}{2 c^{2}}\left[\ddot{\lambda}+\frac{1}{2}(\dot{\lambda})^{2}-\frac{1}{2} \dot{\lambda}\dot{\nu}\right]\\R_{0}^{1}&=\frac{1}{c r} e^{-\lambda} \dot{\lambda}\end{aligned}$$

$$T^{\mu\nu}=\rho c^{2}u^{\mu}u^{\nu}$$

对静止点源

$$\rho=M \vec{\delta}^{3} \vec{r}$$

对点源以外，即：$\vec{r}\neq 0, T_{\nu}^{\mu}=0$，故Einstein张量化为

$$R_{\nu}^{\mu}-\frac{1}{2} \delta_{\nu}^{\mu} R=0$$

4. 中心球对称Einstein方程

在引力物质源外，中心球对称Einstein方程为

$$e^{-\lambda}\left(\frac{1}{r} \nu^{\prime}+\frac{1}{r^{2}}\right)-\frac{1}{r^{2}}=0\tag{3.1}$$

$$\frac{1}{2} e^{-\lambda}\left[\nu^{\prime \prime}+\frac{1}{2}\left(\nu^{\prime}\right)^{2}-\frac{1}{2} \nu^{\prime} \lambda^{\prime}+\frac{1}{r}\left(\nu^{\prime}-\lambda^{\prime}\right)\right]+\frac{1}{2 c^{2}}\left[\ddot{\lambda}+\frac{1}{2}(\dot{\lambda})^{2}-\frac{1}{2} \dot{\lambda} \dot{\nu}\right]=0\tag{3.2}$$

$$e^{-\lambda}\left[\frac{1}{r^{2}}-\frac{1}{r} \lambda^{\prime}\right]-\frac{1}{r^{2}}=0\tag{3.3}$$

$$\frac{1}{c r} e^{-\lambda} \dot{\lambda}=0\tag{3.4}$$

由(3.4)可得

$$\dot{\lambda}=0$$

知$\lambda$与时间无关，即

$$\lambda=\lambda(r)$$

由(3.1)可得

$$\nu^{\prime}=\frac{e^{-\lambda}-1}{r}\tag{3.5}$$

由(3.3)可得

$$\lambda^{\prime}=\frac{1-e^{\lambda}}{r}\tag{3.6}$$

故

$$\lambda^{\prime}+\nu^{\prime}=0\tag{3.7}$$

由$\lambda$与时间无关，(3.2)式化为

$$\nu^{\prime \prime}+\frac{1}{2}\left(\nu^{\prime}\right)^{2}-\frac{1}{2} \nu^{\prime} \lambda^{\prime} + \frac{1}{r}\left(\nu^{\prime}-\lambda^{\prime}\right)=0\tag{3.8}$$

(3.7)说明

$$\lambda+\nu=f(t)\tag{3.9}$$

但$\lambda$不是$t$的函数，故

$$\frac{\partial \nu}{\partial t}=\frac{\partial f(t)}{\partial t}$$

即

$$\frac{\partial}{\partial t}(\nu-f(t))=0$$

因而有

$$\nu-f(t)=\overline{\nu}(r)\tag{3.10}$$

做时间尺度变化

$$\overline{t}=\psi(t)$$

则

$$(\mathrm{d} \overline{t})^{2}=\left(\frac{\mathrm{d} \psi}{\mathrm{d} t}\right)^{2}(\mathrm{d} t)^{2}$$

则如果选$\psi(t)$满足

$$\left(\frac{\mathrm{d} \psi}{\mathrm{d} t}\right)^{2}=e^{f(t)}$$

则

$$(\mathrm{d} \overline{t})^{2}=e^{f(t)}(\mathrm{d} t)^{2}$$

即

$$(d t)^{2}=e^{-f(t)}(d \overline{t})^{2}$$

因此

$$e^{\nu}(d t)^{2}=e^{\nu-f(t)}(d \overline{t})^{2}=e^{\overline{\nu}}(d \overline{t})^{2}$$

由(3.9)和(3.10})知

$$e^{-\lambda}=e^{\nu}$$

下面解$e^{-\lambda}$。方程(3.6)为

$$\frac{\mathrm{d} \lambda}{\mathrm{d} r}=\frac{1-e^{\lambda}}{r}$$

$$e^{-\lambda} \frac{\mathrm{d} \lambda}{\mathrm{d} r}=\frac{e^{-\lambda}-1}{r}$$

$$-\frac{\mathrm{d} e^{-\lambda}}{\mathrm{d} r}=\frac{e^{-\lambda}-1}{r}$$

则

$$\frac{\mathrm{d}\left(e^{-\lambda}-1\right)}{e^{-\lambda}-1}+\frac{\mathrm{d} r}{r}=0$$

$$\ln \left(e^{-\lambda}-1\right)+\ln r=\ln \alpha$$

由此可得

$$\left(e^{-\lambda}-1\right) r=\alpha$$

则

$$e^{-\lambda}=1+\frac{\alpha}{r}$$

最后得到

$$\epsilon^{-\lambda}=e^{\nu}=1+\frac{\alpha}{r}, \quad \lambda+\nu=0$$

可证明(3.5)、(3.7)与(3.8)是自洽的。

5. 积分常数$\alpha$的确定

由于

$$g_{00}=-e^{-\nu}=-\left(1-\frac{2 G M}{r c^{2}}\right)$$

即

$$e^{-\nu}=1-\frac{2 G M}{r c^{2}}$$

因

$$e^{\nu}=1+\frac{\alpha}{r}$$

比较上两式可得

$$\alpha=-\frac{2 G M}{c^{2}}$$

是一小量，并且

$$e^{\lambda}=\frac{1}{1-\frac{2 G M}{c^{2} r}}$$

因此中心球对称Einstein方程解对应的弧元为

$$\mathrm{d} s^{2}=c^{2} e^{\nu} \mathrm{d} t^{2}-r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)-e^{\lambda} \mathrm{d} r^{3}$$

可化为

$$\mathrm{d} s^{2}=c^{2}\left(1-\frac{2 G M}{c^{2} r}\right) \mathrm{d} t^{2}-r^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)-\frac{1}{1-\frac{2 G M}{c^{2} r}} \mathrm{d} r^{2}$$

1916年Schwarzschild首先求得上述Einstein方程的中心球对称度规解，称为Schwarzschild度规。

$\frac{2GM}{c^{2}}$具有长度量纲，定义

$$r_{S}=\frac{2GM}{c^{2}}$$

$r_{S}$称为Schwarzschild半径。对太阳

$$M_{\odot}=1.991 \times 10^{33}g,\quad r_{\odot}=695700km$$

计算得

$$r_{S}=\frac{2 G M}{c^{2}}=2.9532km$$

$$\frac{r_{S}}{r_{\odot}}=\frac{2 G M}{c^{2} r_{\odot}}=4.245 \times 10^{-6}$$