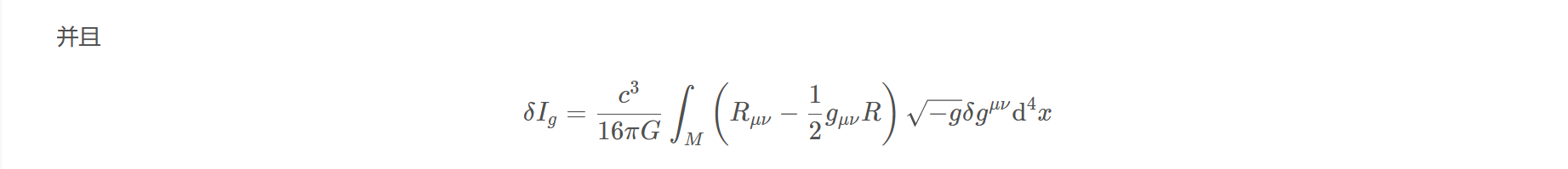物理

【广义相对论速成版】2. Einstein引力场方程 2.6 Einstein引力场方程的作用量

1. $R_{\mu\nu}$变分的Palatini公式(1919)

首先证明$\Gamma_{\mu\nu}^{\rho}$对$g_{\mu\nu}$的变分是一个张量。

由于

$$\Gamma_{\mu \nu}^{\prime\rho}=\overline{A}_{\mu}^{\lambda} \overline{A}_{\nu}^{\tau} A_{\sigma}^{\rho} \Gamma_{\lambda \tau}^{\sigma}+\overline{A}_{\mu}^{\lambda} A_{\sigma}^{\rho} \frac{\partial \overline{A}_{\nu}^{\sigma}}{\partial x^{\lambda}}$$

因变换矩阵$\overline{A}$和$A$与$g_{\mu\nu}$无关，故

$$\delta \Gamma_{\mu \nu}^{\prime \rho}=\overline{A}_{\mu}^{\lambda} \overline{A}_{\nu}^{\tau} A_{\sigma}^{\rho} \delta \Gamma_{\lambda \tau}^{\sigma}$$

即$\delta\Gamma_{\mu\nu}^{\rho}$是按张量变化的，它是三阶混合张量。因

$$R_{\mu \nu}=\partial_{\lambda} \Gamma_{\mu \nu}^{\lambda}-\partial_{\nu} \Gamma_{\lambda \mu}^{\lambda}+\Gamma_{\lambda \rho}^{\lambda} \Gamma_{\mu \nu}^{\rho}-\Gamma_{\nu \rho}^{\lambda} \Gamma_{\mu \lambda}^{\rho}$$

故$R_{\mu\nu}$对$g_{\mu\nu}$的变分

$$\delta R_{\mu\nu}=\partial_{\lambda}\left(\delta\Gamma_{\mu \nu}^{\lambda}\right)-\partial_{\nu} \delta\left(\Gamma_{\lambda \mu}^{\lambda}\right)+\left(\delta \Gamma_{\lambda p}^{\lambda}\right) \Gamma_{\mu \nu}^{\rho}+\Gamma_{\lambda \rho}^{\lambda}\left(\delta\Gamma_{\mu\nu}^{\rho}\right)-\left(\delta \Gamma_{\nu \rho}^{\lambda}\right) \Gamma_{\mu \lambda}^{\rho}-\Gamma_{\nu \rho}^{\lambda}\left(\delta \Gamma_{\mu \lambda}^{\rho}\right)$$

由于

$$\nabla_{\nu}\left(\delta \Gamma_{\lambda \mu}^{\lambda}\right)=\partial_{\nu} \delta\left(\Gamma_{\lambda \mu}^{\lambda}\right)-\Gamma_{\mu \nu}^{\rho}\delta \Gamma_{\lambda p}^{\lambda}$$

$$\nabla_{\lambda}\left(\delta \Gamma_{\mu \nu}^{\lambda}\right)=\partial_{\lambda}\left(\delta\Gamma_{\mu \nu}^{\lambda}\right)+\Gamma_{\lambda \rho}^{\lambda}\delta\Gamma_{\mu\nu}^{\rho}-\Gamma_{\lambda \mu}^{\rho}\delta \Gamma_{\rho \nu}^{\lambda} -\Gamma_{\lambda \nu}^{\rho}\delta \Gamma_{\mu \rho}^{\lambda}$$

由此得到Palatini公式I

$$\delta R_{\mu \nu}=\nabla_{\lambda}\left(\delta \Gamma_{\mu \nu}^{\lambda}\right)-\nabla_{\nu}\left(\delta \Gamma_{\lambda \mu}^{\lambda}\right),\qquad \text{\textbf{Palatini公式 I}}$$

由此可知

$$g^{\mu \nu} \delta R_{\mu \nu}=\nabla_{\lambda}\left(g^{\mu \nu} \delta \Gamma_{\mu \nu}^{\lambda}\right)-\nabla_{\nu}\left(g^{\mu \nu} \delta \Gamma_{\lambda \mu}^{\lambda}\right)=\nabla_{\mu}\left(g^{\lambda \nu} \delta \Gamma_{\lambda \nu}^{\mu}\right)-\nabla_{\mu}\left(g^{\nu \mu} \delta \Gamma_{\lambda \nu}^{\lambda}\right)$$

故

$$g^{\mu \nu} \delta R_{\mu \nu}=\nabla_{\mu}\left[g^{\lambda \nu}\left(\delta \Gamma_{\lambda \nu}^{\mu}\right)-g^{\mu \nu} \delta\left(\Gamma_{\lambda \nu}^{\lambda}\right)\right]$$

令

$$\phi^{\mu}=g^{\lambda \nu}\left(\delta \Gamma_{\lambda \nu}^{\mu}\right)-g^{\mu \nu} \delta\left(\Gamma_{\lambda \nu}^{\lambda}\right)$$

则

$$g^{\mu \nu} \delta R_{\mu \nu}=\nabla_{\mu} \phi^{\mu}=\frac{1}{\sqrt{-g}} \partial_{\mu}\left(\sqrt{-g} \phi^{\mu}\right)$$

因此

$$\sqrt{-g} g^{\mu \nu} \delta R_{\mu \nu} = \partial_{\mu}\left(\sqrt{-g} \phi^{\mu}\right),\qquad \text{\textbf{Palatini公式 II}}$$

即

$\sqrt{-g} g^{\mu \nu} \delta R_{\mu \nu}$可表示为$\sqrt{-g} \phi^{\mu}$的散度。

2. $R\sqrt{-g}$变分与Einstein张量

$R \sqrt{-g}$对$g_{\mu \nu}$的变分如下：

由于

$$R=g^{\mu \nu} R_{\mu \nu}$$

$$R \sqrt{-g}=g^{\mu \nu} R_{\mu \nu} \sqrt{-g}$$

则

$$\delta(R \sqrt{-g})=\left(\delta g^{\mu \nu}\right) R_{\mu \nu} \sqrt{-g}+g^{\mu \nu}\left(\delta R_{\mu \nu}\right) \sqrt{-g}+g^{\mu \nu} R_{\mu \nu}(\delta \sqrt{-g})$$

因

$$\sqrt{-g} g^{\mu \nu}\left(\delta R_{\mu \nu}\right)=\partial_{\mu}\left(\sqrt{-g} \phi^{\mu}\right)$$

$$\delta g=\left(\delta g_{\mu \nu}\right) g^{\mu \nu} g=-g_{\mu \nu^{\prime}}\left(\delta g^{\mu \nu}\right) g$$

$$\delta \sqrt{-g}=-\frac{1}{2} \frac{1}{\sqrt{-g}} \delta g=\frac{1}{2} \frac{1}{\sqrt{-g}} g_{\mu \nu}\left(\delta g^{\mu \nu}\right) g=-\frac{1}{2} \sqrt{-g} g_{\mu \nu}\left(\delta g^{\mu \nu}\right)$$

由此可得

$$g^{\mu \nu} R_{\mu \nu}(\delta \sqrt{-g})=-g^{\mu \nu} R_{\mu \nu} \frac{1}{2} \sqrt{-g} g_{\mu \nu}\left(\delta g^{\mu \nu}\right)=-\frac{1}{2} R \sqrt{-g} g_{\mu \nu}\left(\delta g^{\mu \nu}\right)$$

故

$$\delta(R \sqrt{-g})=\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right) \sqrt{-g} \delta g^{\mu \nu}+\partial_{\mu}\left(\sqrt{-g} \phi^{\mu}\right)$$

引力场作用量的变分

$$\delta \int_{M} R \sqrt{-g} d^{4} x=\int_{M}\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right) \sqrt{-g} \delta g^{\mu \nu} \mathrm{d}^{4} x+\int_{M} \partial_{\mu}\left(\sqrt{-g \phi^{\mu}}\right) \mathrm{d}^{4} x$$

上式第二项化为超曲面上$\sqrt{-g}\phi^{\mu}$的积分，$\phi^{\mu}$和$g_{\mu\nu}$的变分有关，此项在变分法理论中应为零，故

$$\delta \int_{M} R \sqrt{-g} \mathrm{d}^{4} x=\int_{M}\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right) \sqrt{-g} \delta g^{\mu \nu} \mathrm{d}^{4} x$$

这说明$R\sqrt{-g}$与运动方程有关，的确可得到Einstein张量，这是它的本质。因此，引力场方程的作用量可表示为

$$I_{g}=\frac{c^{3}}{16 \pi G} \int_{M} R \sqrt{-g} \mathrm{d}^{4} x$$

乘上系数$\frac{c^{3}}{16\pi G}$是为了使$I_{g}$具有作用量的量纲

$$[R]=[L]^{-2}$$

$$[G]=[M]^{-1}[L]^{3}[T]^{-2}$$

$$I_{g}=\left[c\right]^{3}[G]^{-1}[R]\left[\mathrm{d}^{4} x\right]=[L]^{3}[T]^{-3}[M][L]^{-3}[T]^{2}[L]^{-2}[L]^{4}=[M][L]^{2}[T]^{-1}$$

恰好是作用量的量纲。故

$$I_{g}=\int_{M} L_{g} \sqrt{-g} \mathrm{d}^{4} x$$

因此引力场的Lagrangian $L_{g}$为

$$L_{g}=\frac{c^{3}}{16 \pi G} R$$

并且

$$\delta I_{g}=\frac{c^{3}}{16 \pi G} \int_{M}\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right) \sqrt{-g} \delta g^{\mu \nu} \mathrm{d}^{4} x$$

3. Einstein引力场方程的作用量

设引力场和引力源物质的作用量分别为$I_{g}$和$I_{m}$

$$I_{g}=\int_{M} L_{g} \sqrt{-g} \mathrm{d}^{4} x, \quad L_{g}=\frac{c^{3}}{16 \pi G} R$$

$$I_{n}=\int_{M} L_{n} \sqrt{-g} \mathrm{d}^{4} x$$

令

$$L_{m}=-\frac{\Lambda}{c}$$

$\Lambda$不含$g_{\mu\nu}$的微商

$$I_{m}=\frac{1}{c} \int_{M} \Lambda \sqrt{-g} \mathrm{d}^{4} x$$

则

$$\delta I_{m}=\frac{1}{c} \int_{M} \frac{\delta(\Lambda \sqrt{-g})}{\delta g_{\mu \nu}} \delta g_{\mu \nu} \mathrm{d}^{4} x$$

定义

$$T_{\mu \nu}=\frac{2}{\sqrt{-g}} \cdot \frac{\delta(\Lambda \sqrt{-g})}{\delta g_{\mu \nu}}$$

则

$$\delta I_{m}=\frac{1}{2 c} \int_{M} T_{\mu \nu} \delta q_{\mu \nu} \sqrt{-g} \mathrm{d}^{4} x$$

由

$$\delta I_{m}=\delta I_{g}+\delta I_{m}=\frac{c^{3}}{16 \pi G} \int_{M}\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right) \sqrt{-g} \delta g^{\mu \nu} \mathrm{d}^{4} x+\frac{1}{2 c} \int_{M} T_{\mu \nu} \delta g_{\mu \nu} \sqrt{-g} \mathrm{d}^{4}x$$

由最小作用量原理

$$\frac{c^{3}}{16 \pi G}\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right)+\frac{1}{2 c} T_{\mu \nu}=0$$

由此可得Einstein引力场方程

$$R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R=-\frac{8 \pi G}{c^{4}} T_{\mu \nu}$$