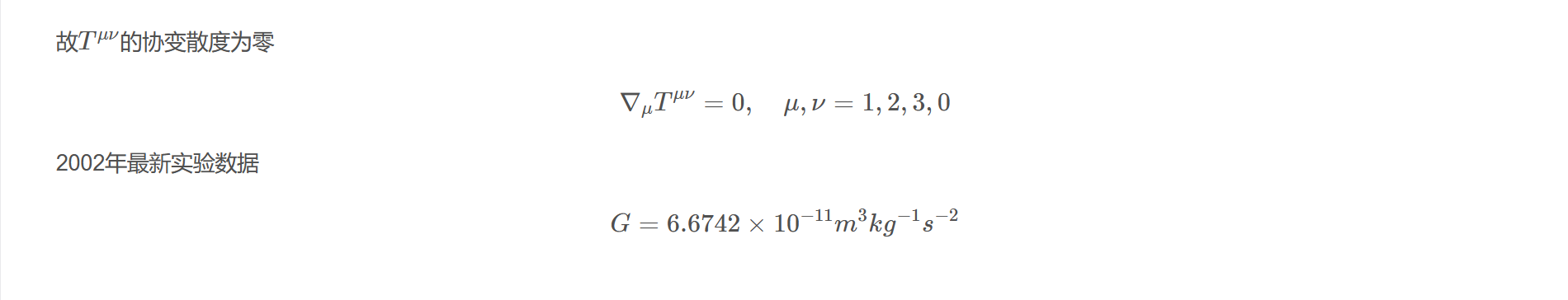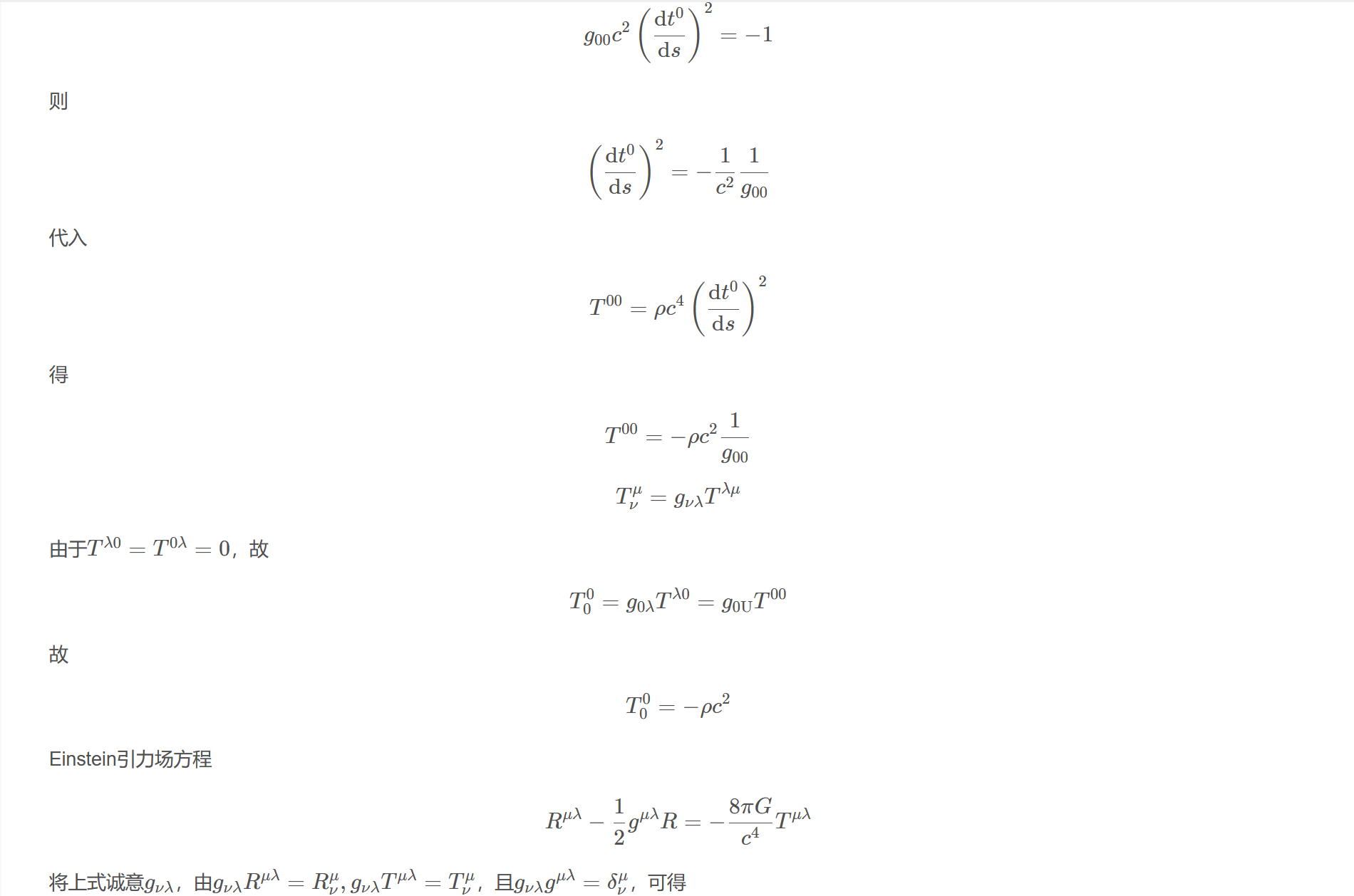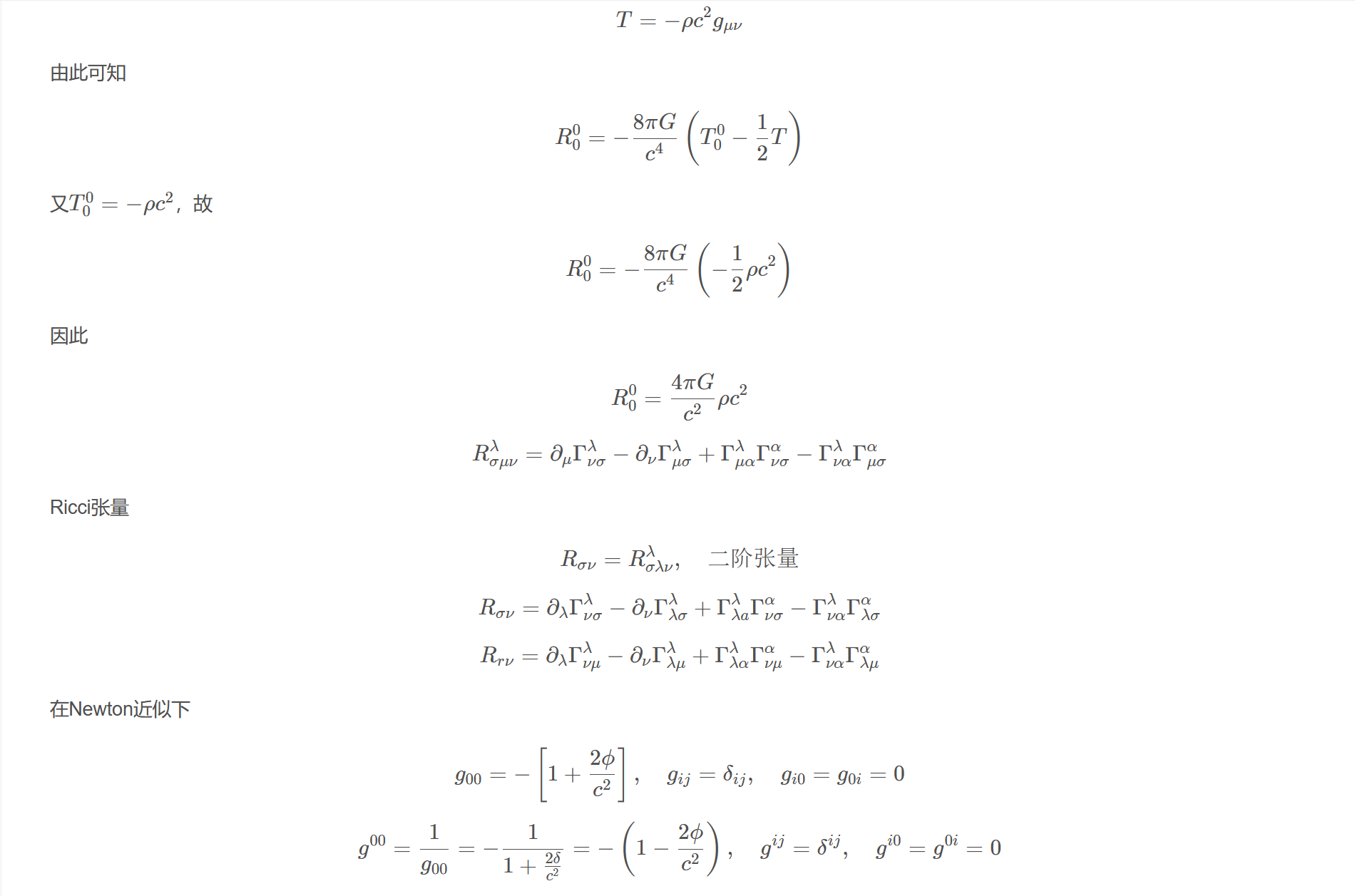物理

【广义相对论速成版】2. Einstein引力场方程 2.4 Einstein引力场方程

1. Einstein引力场方程的建立

Einstein引力场方程是广义相对论的核心，它是在以下几个假设的基础上建立起来的：

(1) 有引力场存在的时空为四维Riemann流形，即：度规张量$g_{\mu\nu}$描述引力场的函数，$g_{\mu\nu}$共有$10$个分量;

(2) 产生引力场的物质源(引力场以外的，引力场也是物质，哲学上所有客观存在都是物质)为物质的能量、动量张量$T^{\mu\nu}$，它是Riemann上的二级对称张量;

(3) 引力场方程是由Riemann曲率张量组成的Einstein张量

$$G^{\mu \nu}=R^{\mu \nu}-\frac{1}{2} g^{\mu \nu} R$$

构成的，与$T^{\mu\nu}$成正比

$$R^{\mu \nu}-\frac{1}{2} g^{\mu \nu} R=\frac{8 \pi G}{c^{4}} T^{\mu \nu}$$

$G$为万有引力常数，成为Einstein引力场方程，它是$g_{\mu\nu}$的二阶非线性偏微分方程。

由Bianchi等式知道

$$\nabla_{i^{2}} G^{\mu \nu}=\nabla_{\mu}\left(R^{\mu \nu}-\frac{1}{2} g^{\mu \nu} R\right)=0$$

故$T^{\mu\nu}$的协变散度为零

$$\nabla_{\mu} T^{\mu \nu}=0, \quad \mu, \nu=1,2,3,0$$

2002年最新实验数据

$$G=6.6742 \times 10^{-11} m^{3} k g^{-1} s^{-2}$$

2. $\nabla_{\mu}T^{\mu\nu}=0$的内涵

$\nabla_{\mu}T^{\mu\nu}=0$与能量动量守恒定律有关，它还隐含物质运动方程，$T^{\mu\nu}$是产生引力场的物质源，但当一个质点在引力场$g_{\mu\nu}$中运动时

$$T^{\mu \nu}=\rho c^{2} u^{\mu} u^{\nu}, \quad \rho=m \delta^{3}(x-x(s)), \quad u^{\mu}=\frac{\mathrm{d} x^{\mu}}{\mathrm{d} s}$$

$$\nabla_{\mu}\left(\rho c^{2} u^{\mu} u^{\nu}\right)=0$$

$$\nabla_{\mu}\left(\rho c^{2} u^{\mu}\right) u^{\nu}+u^{\mu} \nabla_{\mu}\left(\rho c^{2} u^{\nu}\right)=0$$

$\rho u^{\mu}$为质点的物质密度流

$$j^{\mu}=\rho u^{\mu}$$

若$j^{\mu}$为守恒流

$$\nabla j^{\mu}=0$$

则

$$u^{\mu} \nabla_{\mu} u^{\nu}=0$$

或改写为

$$u^{\mu} \nabla_{\mu} u^{\lambda}=0, \quad \lambda=1,2,3,0$$

$$u^{\mu}\left(\partial_{\mu} u^{\lambda}+\Gamma_{\mu \nu}^{\lambda} u^{\nu}\right)=0$$

$$u^{\mu} \partial_{\mu} u^{\lambda}+\Gamma_{\mu \nu}^{\lambda} u^{\mu} u^{i \nu}=0$$

但因

$$u^{\prime \prime}=\frac{\mathrm{d} x^{\mu}}{\mathrm{d} s}$$

$$u^{\mu} \partial_{\mu} u^{\lambda}=\frac{\mathrm{d} x^{\mu}}{\mathrm{d} s} \frac{\partial u^{\lambda}}{\partial x^{\mu}}=\frac{\mathrm{d} u^{\lambda}}{\mathrm{d} s}$$

故

$$\frac{\mathrm{d} u^{\lambda}}{\mathrm{d} s}+\Gamma_{\mu \nu}^{\lambda} u^{\mu} u^{\nu}=0$$

将$u^{\lambda}=\frac{\mathrm{d}x^{\lambda}}{\mathrm{d}s}$代入上式

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} s^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} s} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} s}=0$$

此即短程线方程也。因此质点运动规律是短程线。从这个观点看，前一节内容也不是假设，它包含在Einstein引力场方程之内。

3. Newton近似下的静态引力场方程

考虑引力源能量动量张量

$$T^{\mu \nu}=\rho c^{2} u^{\mu} u^{\nu}$$

$\rho$为引力物质源质量密度

$$u^{\mu}=\frac{\mathrm{d} x^{\mu}}{\mathrm{d} s}$$

对静止源，$u^{i}=0,i=1,2,3$，故$T^{\mu\nu}$中不为零的分量仅有

$$T^{00}=\rho c^{2} u^{0} u^{0}=\rho c^{2} \frac{\mathrm{d} x^{0}}{\mathrm{d} s} \frac{\mathrm{d} x^{0}}{\mathrm{d} s}, \quad x^{0}=c t$$

即

$$T^{00}=\rho c^{4}\left(\frac{\mathrm{d} t^{0}}{\mathrm{d} s}\right)^{2}$$

由于

$$\mathrm{d} s^{2}=-g_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}$$

$$g_{\mu \nu} u^{\mu} u^{\nu}=-1, \quad u^{\mu}=\frac{\mathrm{d} x^{\mu}}{\mathrm{d} s}$$

$u^{i}=0,i=1,2,3$时

$$g_{00} \frac{\mathrm{d} x^{0}}{\mathrm{d} s} \frac{\mathrm{d} x^{0}}{\mathrm{d} s}=-1$$

由于$x^{0}=ct$

$$g_{00} c^{2}\left(\frac{\mathrm{d} t^{0}}{\mathrm{d} s}\right)^{2}=-1$$

则

$$\left(\frac{\mathrm{d} t^{0}}{\mathrm{d} s}\right)^{2}=-\frac{1}{c^{2}} \frac{1}{g_{00}}$$

代入

$$T^{00}=\rho c^{4}\left(\frac{\mathrm{d} t^{0}}{\mathrm{d} s}\right)^{2}$$

得

$$T^{00}=-\rho c^{2} \frac{1}{g_{00}}$$

$$T_{\nu}^{\mu}=g_{\nu \lambda} T^{\lambda \mu}$$

由于$T^{\lambda 0}=T^{0\lambda}=0$，故

$$T_{0}^{0}=g_{0 \lambda} T^{\lambda 0}=g_{0 \mathrm{U}} T^{00}$$

故

$$T_{0}^{0}=-\rho c^{2}$$

Einstein引力场方程

$$R^{\mu \lambda}-\frac{1}{2} g^{\mu \lambda} R=-\frac{8 \pi G}{c^{4}} T^{\mu \lambda}$$

将上式诚意$g_{\nu\lambda}$，由$g_{\nu\lambda}R^{\mu\lambda}=R_{\nu}^{\mu},g_{\nu\lambda}T^{\mu\lambda}=T_{\nu}^{\mu}$，且$g_{\nu\lambda}g^{\mu\lambda}=\delta_{\nu}^{\mu}$，可得

$$R_{\nu}^{\mu}-\frac{1}{2} \delta_{\nu}^{\mu} R=-\frac{8 \pi G}{c^{4}} T_{\nu}^{\mu}$$

则

$$R_{\mu}^{\mu}-\frac{1}{2} \delta_{\mu}^{\mu} R=-\frac{8 \pi G}{c^{4}} T_{\mu}^{\mu}$$

令$T_{\mu}^{\mu}=T$，且

$$R_{\mu}^{\mu}=g_{\mu \lambda} R^{\mu \lambda}=R$$

由此可将Einstein方程化为

$$R-2 R=-\frac{8 \pi G}{c^{4}} T,\quad \delta_{\mu}^{\mu}\text{中}\mu\text{求和}$$

故

$$R=\frac{8 \pi G}{c^{4}} T$$

$$R_{\nu}^{\mu}=-\frac{8 \pi G}{c^{4}}\left(T_{\nu}^{\mu}-\frac{1}{2} \delta_{\nu}^{\mu} T\right)$$

对前面的

$$T^{\mu \nu}=\rho c^{2} u^{\mu} u^{\nu}$$

故

$$T=g_{i \nu} T^{\mu \nu}=\rho c^{2} g_{\mu \nu} u^{\mu} u^{\nu}$$

可得

$$T=-\rho c^{2} g_{\mu \nu}$$

由此可知

$$R_{0}^{0}=-\frac{8 \pi G}{c^{4}}\left(T_{0}^{0}-\frac{1}{2} T\right)$$

又$T_{0}^{0}=-\rho c^{2}$，故

$$R_{0}^{0}=-\frac{8 \pi G}{c^{4}}\left(-\frac{1}{2} \rho c^{2}\right)$$

因此

$$R_{0}^{0}=\frac{4 \pi G}{c^{2}} \rho c^{2}$$

$$R_{\sigma \mu \nu}^{\lambda}=\partial_{\mu} \Gamma_{\nu \sigma}^{\lambda}-\partial_{\nu} \Gamma_{\mu \sigma}^{\lambda}+\Gamma_{\mu \alpha}^{\lambda} \Gamma_{\nu \sigma}^{\alpha}-\Gamma_{\nu \alpha}^{\lambda} \Gamma_{\mu \sigma}^{\alpha}$$

Ricci张量

$$R_{\sigma \nu}=R_{\sigma \lambda \nu}^{\lambda},\quad \text{二阶张量}$$

$$R_{\sigma \nu}=\partial_{\lambda} \Gamma_{\nu \sigma}^{\lambda}-\partial_{\nu} \Gamma_{\lambda \sigma}^{\lambda}+\Gamma_{\lambda a}^{\lambda} \Gamma_{\nu \sigma}^{\alpha}-\Gamma_{\nu \alpha}^{\lambda} \Gamma_{\lambda \sigma}^{\alpha}$$

$$R_{r \nu}=\partial_{\lambda} \Gamma_{\nu \mu}^{\lambda}-\partial_{\nu} \Gamma_{\lambda \mu}^{\lambda}+\Gamma_{\lambda \alpha}^{\lambda} \Gamma_{\nu \mu}^{\alpha}-\Gamma_{\nu \alpha}^{\lambda} \Gamma_{\lambda \mu}^{\alpha}$$

在Newton近似下

$$g_{00}=-\left[1+\frac{2 \phi}{c^{2}}\right], \quad g_{i j}=\delta_{i j}, \quad g_{i 0}=g_{0 i}=0$$

$$g^{00}=\frac{1}{g_{00}}=-\frac{1}{1+\frac{2 \delta}{c^{2}}}=-\left(1-\frac{2 \phi}{c^{2}}\right), \quad g^{i j}=\delta^{i j}, \quad g^{i 0}=g^{0 i}=0$$

在Newton近似下$\Gamma_{\mu\nu}^{\lambda}$不为零的分量仅有

$$\Gamma_{00}^{i}=-\frac{1}{2} \partial_{i} h_{00}, \quad \Gamma_{0 i}^{0}=-\frac{1}{2} \partial_{i} h_{00}, \quad h_{00}=-\frac{2 \phi}{c^{2}}$$

故不为零的$\Gamma_{\mu\nu}^{\lambda}$为

$$\Gamma_{00}^{i}=\frac{1}{c^{2}} \partial_{i} \phi, \quad \Gamma_{0 i}^{0}=\frac{1}{c^{2}} \partial_{i} \phi$$

从$R_{\mu\nu}$式，$\mu,\nu=0$时

$$R_{00}=\partial_{\lambda} \Gamma_{00}^{\lambda}-\partial_{0} \Gamma_{\lambda 0}^{\lambda}+\Gamma_{\lambda \alpha}^{\lambda} \Gamma_{00}^{\alpha}-\Gamma_{0 \alpha}^{\lambda} \Gamma_{\lambda 0}^{\alpha}$$

静态情况，$\phi$与时间无关，$\Gamma_{\mu\nu}^{\lambda}$与时间无关，则在Newton近似下

$$R_{00}=\partial_{i} \Gamma_{00}^{i}-0+\Gamma_{0 i}^{0} \Gamma_{00}^{i}-\Gamma_{0 i}^{0} \Gamma_{00}^{i}-\Gamma_{00}^{i} \Gamma_{i 0}^{0}$$

略去$\frac{\phi}{c^{2}}$的平方项，则

$$R_{00}=\partial_{i} \Gamma_{00}^{i}=\frac{1}{c^{2}} \partial_{i} \partial_{i} \phi$$

即

$$R_{00}=\frac{1}{c^{2}} \Delta \phi, \quad \Delta=\partial_{i} \partial_{i}$$

$$R_{0}^{0}=g^{00} R_{00}, \quad g^{00}=-\left(1-\frac{2 \phi}{c^{2}}\right)$$

略去$\frac{\phi}{c^{2}}$的高次项

$$R_{0}^{0}=-\frac{1}{c^{2}} \Delta \phi$$

但由于

$$R_{0}^{0}=\frac{4 \pi G}{c^{2}} \rho$$

故$\phi$应满足下列方程

$$\Delta\phi=-4 \pi G \rho$$

对静止的点质量源

$$\rho=M \delta^{3}(\vec{r})$$

故

$$\Delta \phi=4 \pi G M \delta^{3}(\vec{r})$$

由Green函数知

$$\Delta \frac{1}{r}=-4 \pi \delta^{3}(\vec{r})$$

因此，得到

$$\phi=-\frac{G M}{r}$$

故Einstein建立的广义相对论包含了Newton第二定律(短程线)和引力公式，且度规是决定引力场的函数

$$g_{00}=-\left(1+\frac{2 \phi}{c^{2}}\right)=-\left(1-\frac{2 G M}{r c^{2}}\right)$$