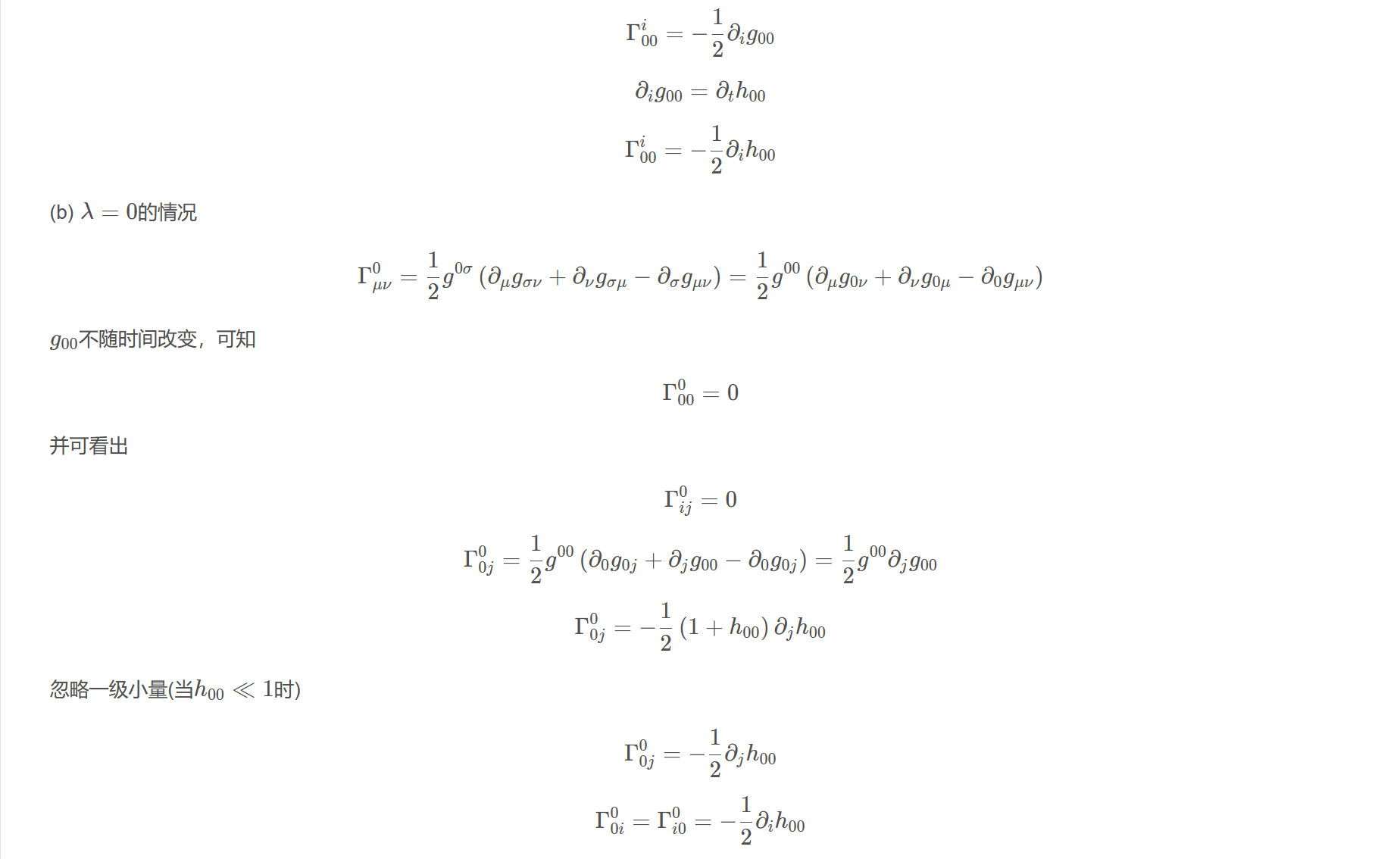物理

【广义相对论速成版】2. Einstein引力场方程 2.3 度规的弱引力场和低速近似与Newton第二定律

1. 弱引力场近似

$$\mathrm{d} s^{2}=-g_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}, \quad \mu, \nu=\{1,2,3,0\}$$

在弱引力场情况可将$g_{\mu\nu}$分解为

$$g_{\mu \nu}=\eta_{\mu \nu}+h_{\mu \nu}$$

其中，$\eta_{\mu\nu}$为平直时空的度规，$h_{\mu\nu}$为$g_{\mu\nu}$对平直时空的偏离，则

$$\begin{aligned} \mathrm{d} s^{2}=&-\eta_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}-h_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}\\=& c^{2} \mathrm{d} t^{2}-\left[\left(\mathrm{d} x^{1}\right)^{2}+\left(\mathrm{d} x^{2}\right)^{2}+\left(\mathrm{d} x^{3}\right)^{2}\right]\\&-\left[c^{2} h_{00} \mathrm{d} t^{2}+2 c h_{0i} \mathrm{d} t \mathrm{d} x^{i}+h_{i j} \mathrm{d} x^{i} \mathrm{d} x^{j}\right]\end{aligned}$$

令

$$v^{i}=\frac{\mathrm{d} x^{i}}{\mathrm{d} t}$$

则

$$\mathrm{d} s^{2}=c^{2} \mathrm{d} t^{2}\left[1-h_{00}-2 h_{0 i} \frac{v^{i}}{c}-h_{i j} \frac{v^{i} v^{j}}{c^{2}}\right]-\left[\left(\mathrm{d} x^{1}\right)^{2}+\left(\mathrm{d} x^{2}\right)^{2}+\left(\mathrm{d} x^{3}\right)^{2}\right]$$

2. Newton近似(弱引力、低速、稳态)

(1) 度规

在弱引力场和低速近似情况，这时

$$\frac{v}{c} \ll 1$$

称为Newton近似，弱引力场，度规$g_{\mu\nu}$与时间无关，$\partial_{0}g_{0}0=0$，在此条件下

$$\mathrm{d} s^{2}=c^{2} \mathrm{d} t^{2}\left[1-h_{00}\right]-\left[\left(\mathrm{d} x^{1}\right)^{2}+\left(\mathrm{d} x^{2}\right)^{2}+\left(\mathrm{d} x^{3}\right)^{2}\right]\tag{2.1}$$

$$\mathrm{d} s^{2}=-g_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}=-g_{i j} \mathrm{d} x^{i} \mathrm{d} x^{j}-g_{i 0} \mathrm{d} x^{i} \mathrm{d} x^{0}-g_{0 i} \mathrm{d} x^{0} \mathrm{d} x^{i}-g_{00} \mathrm{d} x^{0} \mathrm{d} x^{0}\tag{2.2}$$

其中，$\mu,\nu=1,2,3,0$; $i,j=1,2,3$，将(2.1)与(2.2)比较，可得

$$g_{i j}=\delta_{i j}, \quad g_{i 0}=g_{0 i}=0, \quad g_{00}=-\left[1-h_{00}\right]$$

即

$$[g_{\mu\nu}]=\begin{pmatrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & -(1-h_{00})\end{pmatrix}\qquad[g_{\mu\nu}]^{-1}=\begin{pmatrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & -\frac{1}{1-h_{00}}\end{pmatrix}$$

$$g^{i j}=\delta^{i j}, \quad g^{i 0}=g^{0 i}=0, \quad g^{00}=-\frac{1}{1-h_{00}}$$

但当$h_{00}$很小时

$$-\frac{1}{1-h_{00}}=-\left(1+h_{00}\right)$$

忽略二级小量时

$$\left[-\left(1-h_{00}\right)\right]\left[-\left(1+h_{00}\right)\right]=1-h_{00}^{2} \simeq 1$$

(3) Riemann联络(Christoffel符号)

$$\Gamma_{\mu \nu}^{\lambda}=\frac{1}{2} g^{\lambda \sigma}\left(\partial_{\mu} g_{\sigma \nu}+\partial_{\nu} g_{\sigma \mu}-\partial_{\sigma} g_{\mu \nu}\right)$$

(a) $\lambda=i$的情况 ($i,j=1,2,3$)

$$\begin{aligned}\Gamma_{\mu \nu}^{i} &=\frac{1}{2} g^{i \sigma}\left(\partial_{\mu} g_{\sigma \nu}+\partial_{\nu} g_{\sigma \mu}-\partial_{\sigma} g_{\mu \nu}\right) \\ &=\frac{1}{2} g^{i j}\left(\partial_{\mu} g_{j \nu}+\partial_{\nu} g_{j \mu}-\partial_{j} g_{\mu \nu}\right)\end{aligned}$$

$$\Gamma_{l m}^{i}=\frac{1}{2} g^{i j}\left(\partial_{l} g_{j m}+\partial_{m} g_{j l}-\partial_{j} g_{i m}\right), \quad l, m=1,2,3$$

因

$$g^{i j}=\delta^{i j}, \quad g_{i j}=\delta_{i j}$$

故

$$\Gamma_{l m}^{i}=0$$

 同理

$$\Gamma_{0 m}^{i}=\frac{1}{2} g^{i j}\left(\partial_{0} g_{j m}+\partial_{m} g_{j 0}-\partial_{j} g_{0 m}\right), \quad m=1,2,3$$

可证

$$\Gamma_{0 m}^{i}=0, \quad \Gamma_{i 0}^{i}=0$$

$$\Gamma_{00}^{i}=\frac{1}{2} g^{i j}\left(\partial_{0} g_{j 0}+\partial_{0} g_{j 0}-\partial_{j} g_{00}\right)=-\frac{1}{2} \delta^{i j}\left(\partial_{j} g_{00}\right)=-\frac{1}{2} \partial_{i} g_{00}$$

$$\Gamma_{00}^{i}=-\frac{1}{2} \partial_{i} g_{00}$$

$$\partial_{i} g_{00}=\partial_{t} h_{00}$$

$$\Gamma_{00}^{i}=-\frac{1}{2} \partial_{i} h_{00}$$

(b) $\lambda=0$的情况

$$\Gamma_{\mu \nu}^{0}=\frac{1}{2} g^{0 \sigma}\left(\partial_{\mu} g_{\sigma \nu}+\partial_{\nu} g_{\sigma \mu}-\partial_{\sigma} g_{\mu \nu}\right)=\frac{1}{2} g^{00}\left(\partial_{\mu} g_{0 \nu}+\partial_{\nu} g_{0 \mu}-\partial_{0} g_{\mu \nu}\right)$$

$g_{00}$不随时间改变，可知

$$\Gamma_{00}^{0}=0$$

并可看出

$$\Gamma_{i j}^{0}=0$$

$$\Gamma_{0 j}^{0}=\frac{1}{2} g^{00}\left(\partial_{0} g_{0 j}+\partial_{j} g_{00}-\partial_{0} g_{0 j}\right)=\frac{1}{2} g^{00} \partial_{j} g_{00}$$

$$\Gamma_{0 j}^{0}=-\frac{1}{2}\left(1+h_{00}\right) \partial_{j} h_{00}$$

忽略一级小量(当$h_{00}\ll 1$时)

$$\Gamma_{0 j}^{0}=-\frac{1}{2} \partial_{j} h_{00}$$

$$\Gamma_{0 i}^{0}=\Gamma_{i 0}^{0}=-\frac{1}{2} \partial_{i} h_{00}$$

(3) $\frac{\mathrm{d} x^{\mu}}{\mathrm{d} s}$

当$\mathrm{d} s$在质点运动的轨迹上

$$\begin{aligned}\mathrm{d} s^{2} &=c^{2} \mathrm{d} t^{2}\left(1-h_{00}\right)-\left[\left(\mathrm{d} x^{1}\right)^{2}+\left(\mathrm{d} x^{2}\right)^{2}+\left(\mathrm{d} x^{3}\right)^{2}\right] \\ &=c^{2} \mathrm{d} t^{2}\left\{\left(1-h_{00}\right)-\frac{1}{c^{2}}\left[\left(\frac{\mathrm{d} x^{1}}{\mathrm{d} t}\right)^{2}+\left(\frac{\mathrm{d} x^{2}}{\mathrm{d} t}\right)^{2}+\left(\frac{\mathrm{d} x^{3}}{\mathrm{d} t}\right)^{2}\right]\right\}\end{aligned}$$

在Newton近似下

$$\mathrm{d} s^{2}=c^{2} \mathrm{d} t^{2}\left(1-h_{00}\right)$$

故

$$\frac{\mathrm{d} x^{0}}{\mathrm{d} s}=\frac{1}{\sqrt{1-h_{00}}}, \quad \frac{\mathrm{d} x^{i}}{\mathrm{d} s}=\frac{1}{c} \frac{\mathrm{d} x^{i}}{\mathrm{d} t} \frac{1}{\sqrt{1-h_{00}}}$$

这是$\mathrm{d}s$在质点运动的轨迹上的时候。

(4)$\frac{\mathrm{d}^{2} x^{\mu}}{\mathrm{d} s^{2}}$

当$\mathrm{d} s$在质点运动的轨迹上，先讨论$\mu=0$的情况

$$\frac{\mathrm{d} x^{0}}{\mathrm{d} s}=\frac{1}{\sqrt{1-h_{00}}}$$

$$\begin{aligned}\frac{\mathrm{d}^{2} x^{0}}{\mathrm{d} s^{2}} &=\frac{\mathrm{d}}{\mathrm{d} s}\left(\frac{1}{\sqrt{1-h_{00}}}\right) \\ &=-\frac{1}{2}\left(1-h_{00}\right)^{-\frac{3}{2}} \frac{\mathrm{d}}{\mathrm{d} s}\left(1-h_{00}\right) \\ &=\frac{1}{2}\left(1-h_{20}\right)^{-\frac{3}{2}} \frac{\mathrm{d} h_{00}}{\mathrm{d} s}\end{aligned}$$

因$\frac{\partial h_{00}}{\partial x^{0}}=0$

$$\frac{\mathrm{d} h_{0 0}}{\mathrm{d} s}=\frac{\partial h_{00}}{\partial x^{i}} \frac{\mathrm{d} x^{i}}{\mathrm{d} s}=\frac{1}{c} \frac{\mathrm{d} x^{i}}{\mathrm{d} t} \frac{1}{\sqrt{1-h_{00}}} \partial_{i} h_{00}$$

则

$$\frac{\mathrm{d}^{2} x^{0}}{\mathrm{d} s^{2}}=\frac{1}{2}\left(1-h_{06}\right)^{-2} \partial_{i} h_{00} \frac{1}{c} \frac{\mathrm{d} x^{i}}{\mathrm{d} t}$$

故当$\frac{1}{c}\frac{\mathrm{d}x^{i}}{\mathrm{d}t}\ll 1$或$\frac{v}{c}\ll 1$时

$$\frac{\mathrm{d}^{2} x^{0}}{\mathrm{d} s^{2}}=0$$

$\mu=i$的情况

$$\frac{\mathrm{d} x^{i}}{\mathrm{d} s}=\frac{1}{c} \frac{\mathrm{d} x^{i}}{\mathrm{d} t} \frac{1}{\sqrt{1-h_{00}}}$$

$$\begin{aligned}\frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} s^{2}}&=\frac{1}{c}\frac{\mathrm{d}}{\mathrm{d} s}\left(\frac{\mathrm{d} x^{i}}{\mathrm{d} t}\frac{1}{\sqrt{1-h_{00}}}\right)\\&=\frac{1}{c}\frac{\partial}{\partial t}\left(\frac{\mathrm{d} x^{i}}{\mathrm{d} t} \frac{1}{\sqrt{1-h_{00}}}\right)\frac{\mathrm{d} t}{\mathrm{d} s}+\frac{1}{c}\frac{\partial}{\partial x^{j}}\left(\frac{\mathrm{d} x^{i}}{\mathrm{d} t} \frac{1}{\sqrt{1-h_{00}}}\right)\frac{\mathrm{d} x^{j}}{\mathrm{d} s}\\&=\frac{1}{c}\frac{\partial}{\partial t}\left(\frac{\mathrm{d} x^{i}}{\mathrm{d} t} \frac{1}{\sqrt{1-h_{00}}}\right)\frac{\mathrm{d} t}{\mathrm{d} s}+\frac{1}{c}\frac{\partial}{\partial x^{j}}\left( \frac{1}{\sqrt{1-h_{00}}}\right)\frac{\mathrm{d} x^{i}}{\mathrm{d} t}\frac{\mathrm{d} x^{j}}{\mathrm{d} s}\end{aligned}$$

利用

$$\frac{\mathrm{d} t}{\mathrm{d} s}=\frac{1}{c} \frac{1}{\sqrt{1-h_{00}}}$$

当$\frac{1}{c}\frac{\mathrm{d} x^{i}}{\mathrm{d} t}\ll 1$，得

$$\frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} s^{2}}=\frac{1}{c} \frac{\partial}{\partial t}\left(\frac{\mathrm{d} x^{i}}{\mathrm{d} t} \frac{1}{\sqrt{1-h_{00}}}\right) \frac{1}{c \sqrt{1-h_{00}}}$$

即

$$\frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} s^{2}}=\frac{1}{c^{2}} \frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} t^{2}} \frac{1}{1-h_{00}}, \quad i=1,2,3$$

3. Newton近似下的短程线方程

粒子运动的短程线方程为

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} s^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} s} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} s}=0$$

在Newton近似下

$$\frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} s^{2}}=\frac{1}{c^{2}} \frac{1}{1-h_{00}} \frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} t^{2}}, \quad i=1,2,3$$

$$\frac{\mathrm{d} x^{0}}{\mathrm{d} s}=\frac{1}{\sqrt{1-h_{00}}}$$

$$\frac{\mathrm{d}^{2} x^{0}}{\mathrm{d} s^{2}} \longrightarrow 0$$

$$\frac{\mathrm{d} x^{i}}{\mathrm{d} s}=\frac{1}{c \sqrt{1-h_{00}} \mathrm{d} t} \approx \frac{1}{c} \frac{\mathrm{d} x^{i}}{\mathrm{d} t} \ll 1, \quad \frac{\mathrm{d} x^{i}}{\mathrm{d} s} \longrightarrow 0$$

则Newton近似下短程线方程

$$\frac{\mathrm{d}^{2} x^{\lambda}}{\mathrm{d} s^{2}}+\Gamma_{\mu \nu}^{\lambda} \frac{\mathrm{d} x^{\mu}}{\mathrm{d} s} \frac{\mathrm{d} x^{\nu}}{\mathrm{d} s}=0$$

仅有

$$\frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} s^{2}}+\Gamma_{00}^{i} \frac{\mathrm{d} x^{0}}{\mathrm{d} s} \frac{\mathrm{d} x^{0}}{\mathrm{d} s}=0$$

即

$$\frac{1}{c^{2}} \frac{1}{1-h_{00}} \cdot \frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} t^{2}}+\Gamma_{00}^{i} \frac{1}{1-h_{00}}=0$$

故

$$\frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} t^{2}}+c^{2} \Gamma_{00}^{i}=0, \quad i=1,2,3$$

但因

$$\Gamma_{00}^{i}=-\frac{1}{2} \partial_{i} h_{00}$$

故

$$\frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} t^{2}}=\frac{1}{2} c^{2} \partial_{i} h_{00}, \quad i=1,2,3\quad h_{00}\text{为空间坐标的函数}$$

令

$$\frac{1}{2} c^{2} h_{00}=-\phi$$

即

$$g_{00}=-\left(1+\frac{2 \phi}{c^{2}}\right)$$

因此在Newton近似下短程线方程最终化为

$$\frac{\mathrm{d}^{2} x^{i}}{\mathrm{d} t^{2}}=-\partial_{i} \phi\quad i=1,2,3$$

由于$g_{00}$和$h_{00}$是描述引力场的，则$\phi$应是描述引力场的函数。显然$\phi$是Newton引力势时，则上式恰好是质点在引力场中运动的Newton第二定律，因此广义相对论包含了Newton第二定律。且

$$g_{00}=-\left(1+\frac{2 \phi}{c^{2}}\right)$$

则说明度规与引力势之间的关系。