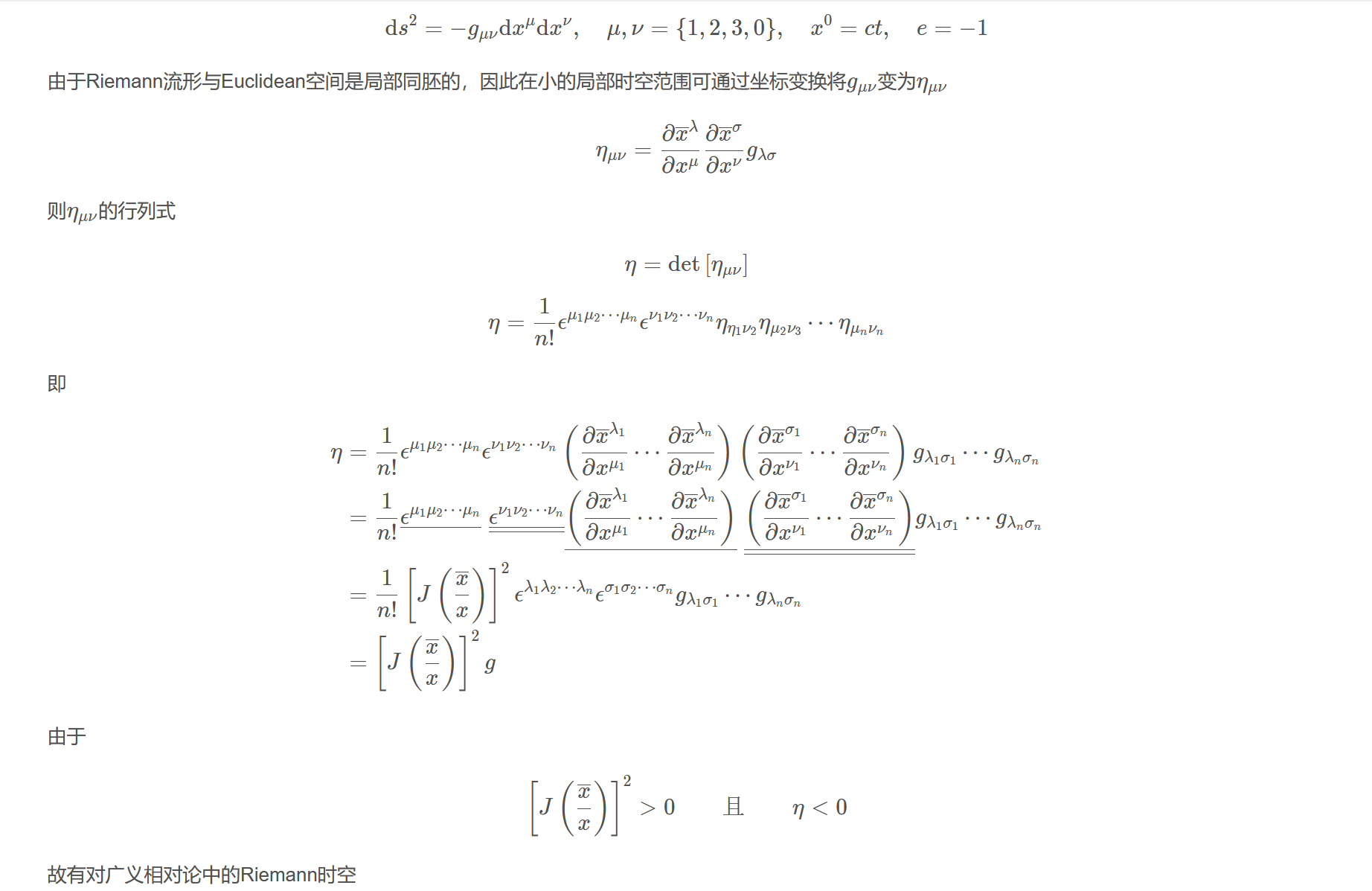物理

【广义相对论速成版】2. Einstein引力场方程 2.1 广义相对论基本原理

1. 基本原理

广义相对论是关于时间空间性质与物质及其运动相互依赖关系的学说，是建立在以下三个基本原理基础上发展起来的引力理论和时空理论。Einstein引力场方程是广义相对论的核心。

(1) 度规是引力场函数

有引力存在的时空是$4-$维Riemann时空流形，其度规张量是描述引力的场的函数，它满足Einstein引力场方程。

(2) 广义协变性原理(广义相对性原理)

物理规律具有广义协变性，即：在任意坐标系物理规律都具有相同的形式，也即：物理规律从对于一切参考系都是平权的，上述原理称为广义协变性原理，也称为广义相对性原理。

(3)等效原理

物质运动规律满足惯性质量与引力质量相等的等效原理。

Newton第二定律，$\vec{F}=m\vec{a}$，$m$称为惯性质量，记为$m_{i}$。

Newton万有引力，$\vec{F}=-\frac{GMm}{r^{3}}\vec{r}$，$m$称为引力质量，记为$m_{g}$。

$$m_{i}=m_{g}$$

还有引力场与惯性力场动力学效应为局部不可分辨的等效原理。

2. 广义相对论中的Riemann时空度规

狭义相对论中时空是平直的，其时空度规和弧元

$$\mathrm{d} s^{2}=c^{2} \mathrm{d} t^{2}-\left[\left(\mathrm{d} x^{1}\right)^{2}+\left(\mathrm{d} x^{2}\right)^{2}+\left(\mathrm{d} x^{3}\right)^{2}\right]$$

即

$$\mathrm{d} s^{2}=c^{2} \mathrm{d} t^{2}\left\{1-\frac{1}{c^{2}}\left[\left(\frac{\mathrm{d} x^{1}}{\mathrm{d} t}\right)^{2}+\left(\frac{\mathrm{d} x^{2}}{\mathrm{d} t}\right)^{2}+\left(\frac{\mathrm{d} x^{3}}{\mathrm{d} t}\right)^{2}\right]\right\}$$

它保证当

$$\left(\frac{\mathrm{d} x^{1}}{\mathrm{d} t}\right)^{2}+\left(\frac{\mathrm{d} x^{2}}{\mathrm{d} t}\right)^{2}+\left(\frac{\mathrm{d} x^{3}}{\mathrm{d} t}\right)^{2}<c^{2}$$

时

$$\mathrm{d} s^{2}>0$$

在狭义相对论中，一般引入下列平直时空度规$\eta_{\mu\nu}$，定义弧元

$$\mathrm{d} s^{2}=-\eta_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}, \quad x^{0}=c t$$

$$\eta_{11}=\eta_{22}=\eta_{33}=1, \quad \eta_{00}=-1, \quad \eta_{0 i}=0, \quad i=1,2,3$$

即

$$\left[\eta_{\mu\nu}\right]=\begin{pmatrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & -1\end{pmatrix},\qquad \det[\eta_{\mu\nu}]=-1$$

在广义相对论中定义Riemann时空度规

$$\mathrm{d} s^{2}=-g_{\mu \nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}, \quad \mu, \nu=\{1,2,3,0\}, \quad x^{0}=c t, \quad e=-1$$

由于Riemann流形与Euclidean空间是局部同胚的，因此在小的局部时空范围可通过坐标变换将$g_{\mu\nu}$变为$\eta_{\mu\nu}$

$$\eta_{\mu\nu}=\frac{\partial \overline{x}^{\lambda}}{\partial x^{\mu}} \frac{\partial \overline{x}^{\sigma}}{\partial x^{\nu}} g_{\lambda \sigma}$$

则$\eta_{\mu\nu}$的行列式

$$\eta=\det\left[\eta_{\mu \nu}\right]$$

$$\eta=\frac{1}{n !} \epsilon^{\mu_{1} \mu_{2} \cdots \mu_{n}} \epsilon^{\nu_{1} \nu_{2} \cdots \nu_{n}} \eta_{\eta_{1} \nu_{2}} \eta_{\mu_{2} \nu_{3}} \cdots \eta_{\mu_{n} \nu_{n}}$$

即

$$\begin{aligned}\eta&=\frac{1}{n!}\epsilon^{\mu_{1}\mu_{2}\cdots\mu_{n}}\epsilon^{\nu_{1}\nu_{2}\cdots\nu_{n}}\left(\frac{\partial \overline{x}^{\lambda_{1}}}{\partial x^{\mu_{1}}}\cdots\frac{\partial \overline{x}^{\lambda_{n}}}{\partial x^{\mu_{n}}}\right)\left(\frac{\partial \overline{x}^{\sigma_{1}}}{\partial x^{\nu_{1}}}\cdots\frac{\partial \overline{x}^{\sigma_{n}}}{\partial x^{\nu_{n}}}\right)g_{\lambda_{1}\sigma_{1}}\cdots g_{\lambda_{n}\sigma_{n}}\\&=\frac{1}{n!}\underline{\epsilon^{\mu_{1}\mu_{2}\cdots\mu_{n}}}~\underline{\underline{\epsilon^{\nu_{1}\nu_{2}\cdots\nu_{n}}}}\underline{\left(\frac{\partial \overline{x}^{\lambda_{1}}}{\partial x^{\mu_{1}}}\cdots\frac{\partial \overline{x}^{\lambda_{n}}}{\partial x^{\mu_{n}}}\right)}~\underline{\underline{\left(\frac{\partial \overline{x}^{\sigma_{1}}}{\partial x^{\nu_{1}}}\cdots\frac{\partial \overline{x}^{\sigma_{n}}}{\partial x^{\nu_{n}}}\right)}}g_{\lambda_{1}\sigma_{1}}\cdots g_{\lambda_{n}\sigma_{n}}\\&=\frac{1}{n!}\left[J\left(\frac{\overline{x}}{x}\right)\right]^{2}\epsilon^{\lambda_{1} \lambda_{2} \cdots \lambda_{n}}\epsilon^{\sigma_{1} \sigma_{2} \cdots \sigma_{n}}g_{\lambda_{1}\sigma_{1}}\cdots g_{\lambda_{n}\sigma_{n}}\\&=\left[J\left(\frac{\overline{x}}{x}\right)\right]^{2}g\end{aligned}$$

由于

$$\left[J\left(\frac{\overline{x}}{x}\right)\right]^{2}>0\qquad \text{且}\qquad \eta<0$$

故有对广义相对论中的Riemann时空

$$g<0$$