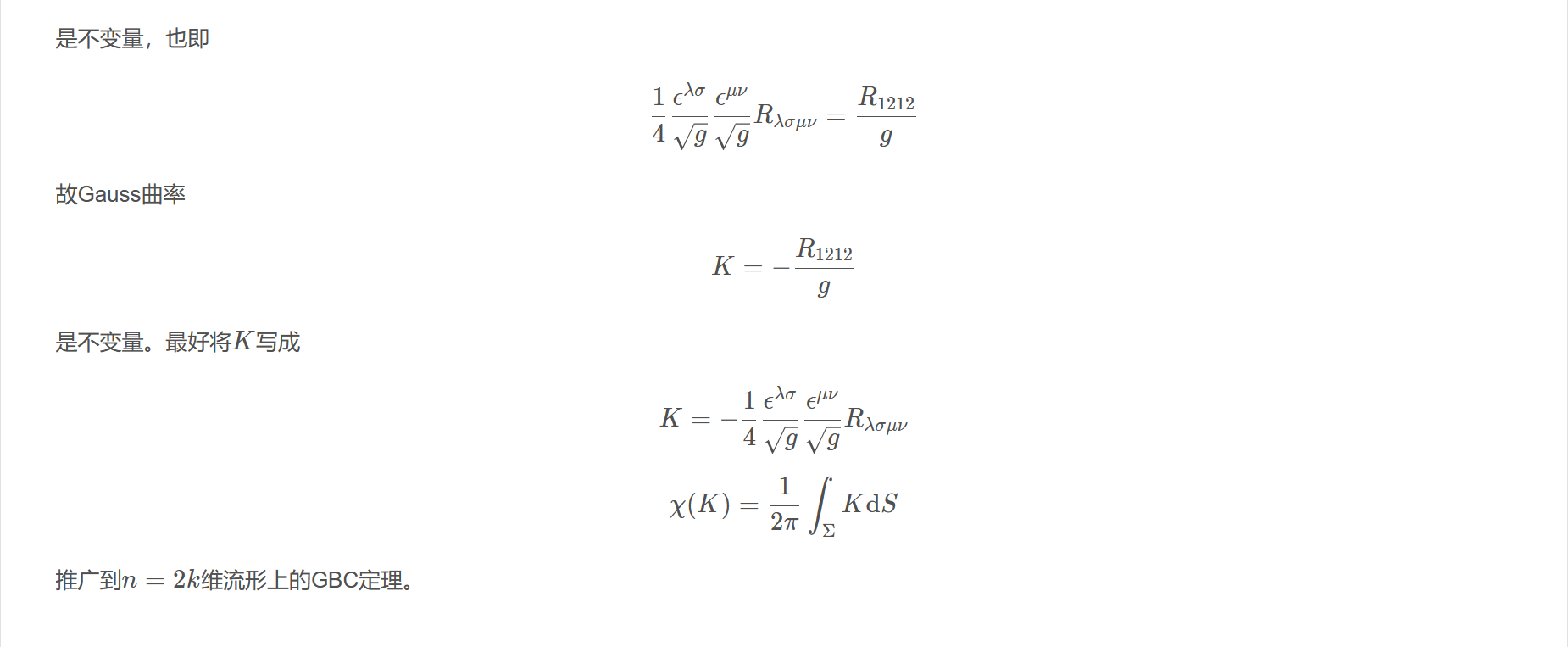物理

【广义相对论速成版】1. Riemann几何 1.9 不变体积元和广义Gauss积分定理

1. 具有协变性的单位反对称张量(Leivi-Civita张量)

由$g_{\mu\nu}$的行列式公式

$$\epsilon^{\mu_{1}\mu_{2}\cdots\mu_{n}}g_{\mu_{1}\nu_{1}}g_{\mu_{2}\nu_{2}}\cdots g_{\mu_{n}\nu_{n}}=g\epsilon_{\nu_{1}\nu_{2}\cdots\nu_{n}}$$

用$g_{\mu\nu}$使$\epsilon^{\mu_{1} \mu_{2} \cdots \mu_{n}}$降指标后$\epsilon^{\mu_{1} \mu_{2} \cdots \mu_{n}}$跟$\epsilon_{\nu_{1} \nu_{2} \cdots \nu_{n}}$都不是一个张量，但可以将上式写成

$$\frac{\epsilon^{\mu_{1} \mu_{2} \cdots \mu_{n}}}{\sqrt{g}} g_{\mu_{1} \nu_{2}} g_{\mu_{2} \nu_{2}} \cdots g_{\mu_{n} \nu_{n}}=\sqrt{g} \epsilon_{\nu_{1} \nu_{2} \cdots \nu_{n}}$$

说明$\frac{\epsilon^{\mu_{1} \mu_{2} \cdots \mu_{n}}}{\sqrt{g}}$是$n$阶单位逆变张量，$\sqrt{g} \epsilon_{\nu_{1} \nu_{2} \cdots \nu_{n}}$是$n$阶单位协变张量。

对一个二维曲面，曲率张量为

$$R_{\lambda \sigma \mu \nu}, \quad \lambda, \sigma, \mu, \nu=\{1,2\}$$

且单位反对称张量为

$$\frac{\epsilon^{\mu \nu}}{\sqrt{g}}, \quad \sqrt{g} \epsilon_{\mu \nu}$$

则

$$\frac{1}{4} \frac{\epsilon^{\lambda \sigma}}{\sqrt{g}} \frac{\epsilon^{\mu \nu}}{\sqrt{g}} R_{\lambda \sigma \mu \nu}$$

是不变量，也即

$$\frac{1}{4} \frac{\epsilon^{\lambda \sigma}}{\sqrt{g}} \frac{\epsilon^{\mu \nu}}{\sqrt{g}} R_{\lambda \sigma \mu \nu}=\frac{R_{1212}}{g}$$

故Gauss曲率

$$K=-\frac{R_{1212}}{g}$$

是不变量。最好将$K$写成

$$K=-\frac{1}{4} \frac{\epsilon^{\lambda \sigma}}{\sqrt{g}} \frac{\epsilon^{\mu \nu}}{\sqrt{g}} R_{\lambda \sigma \mu \nu}$$

$$\chi(K)=\frac{1}{2 \pi} \int_{\Sigma} K \mathrm{d} S$$

推广到$n=2k$维流形上的GBC定理。

2. 不变体积元

由于

$$\mathrm{d} x^{\prime \mu}=A_{\nu}^{\mu} \mathrm{d} x^{\nu}$$

即：$\mathrm{d}x^{\mu}$具有逆变矢量的特征。$n$维流形上的体积元，记为$\mathrm{d}^{n}x$，定义为

$$\mathrm{d}^{n} x=\mathrm{d} x^{1} \wedge \mathrm{d} x^{2} \wedge \cdots \wedge \mathrm{d} x^{n}$$

它对坐标变换不是不变量，但可用$\sqrt{g}\epsilon_{\mu_{1} \mu_{2} \cdots \mu_{n}}$和$\mathrm{d} x^{\mu_{1}} \wedge \mathrm{d} x^{\mu_{2}} \wedge \cdots \wedge \mathrm{d} x^{\mu_{n}}$构成不变体积元

$$\frac{1}{n !} \sqrt{g} \epsilon_{\mu_{1} \mu_{2} \cdots \mu_{n}}\mathrm{d} x^{\mu_{1}} \wedge \mathrm{d} x^{\mu_{2}} \wedge \cdots \wedge \mathrm{d} x^{\mu_{n}}$$

它可写成

$$\sqrt{g}\mathrm{d} x^{1} \wedge \mathrm{d} x^{2} \wedge \cdots \wedge \mathrm{d} x^{n}$$

故$n$维不变体积元应为

$$\sqrt{g}\mathrm{d}^{n}x=\sqrt{g}\mathrm{d} x^{1} \wedge \mathrm{d} x^{2} \wedge \cdots \wedge \mathrm{d} x^{n}$$

3. 广义协变Gauss积分定理

设矢量$j^{\mu}$普通散度为$\partial_{\mu}j^{\mu}$，多变元积分理论已证明存在Gauss定理

$$\int_{M} \partial_{\mu} j^{\mu} \mathrm{d}^{n}x=\int_{\partial M} j^{\mu} \mathrm{d} S_{\mu}$$

$\partial M$为$M$的闭包曲面，$\mathrm{d}S_{\mu}$为$(n-1)$-维面元。

设$J^{\mu}$为一广义逆变矢量，则其协变散度为

$$\nabla_{\mu} J^{\mu}=\frac{1}{\sqrt{g}} \partial_{\mu}\left(\sqrt{g} J^{\mu}\right)$$

由于不变体积元为

$$\sqrt{g} \mathrm{d}^{n} x$$

则

$$\left(\nabla_{\mu}J^{\mu}\right)\sqrt{g}\mathrm{d}^{n}x=\partial_{\mu}\left(J^{\mu}\sqrt{g}\right)\mathrm{d}^{n}x$$

是一个不变量，它在$M$上的不变积分。令$j^{\mu}=\sqrt{g}J^{\mu}$，可知

$$\boxed{\int_{M}\left(\nabla_{\mu} J^{\mu}\right) \sqrt{g} \mathrm{d}^{n} x=\int_{\partial M}  J^{\mu}\sqrt{g} \mathrm{d} S_{\mu}}$$

$\sqrt{g}\mathrm{d}S_{\mu}$称为$\left(n+1\right)$维协变面元。