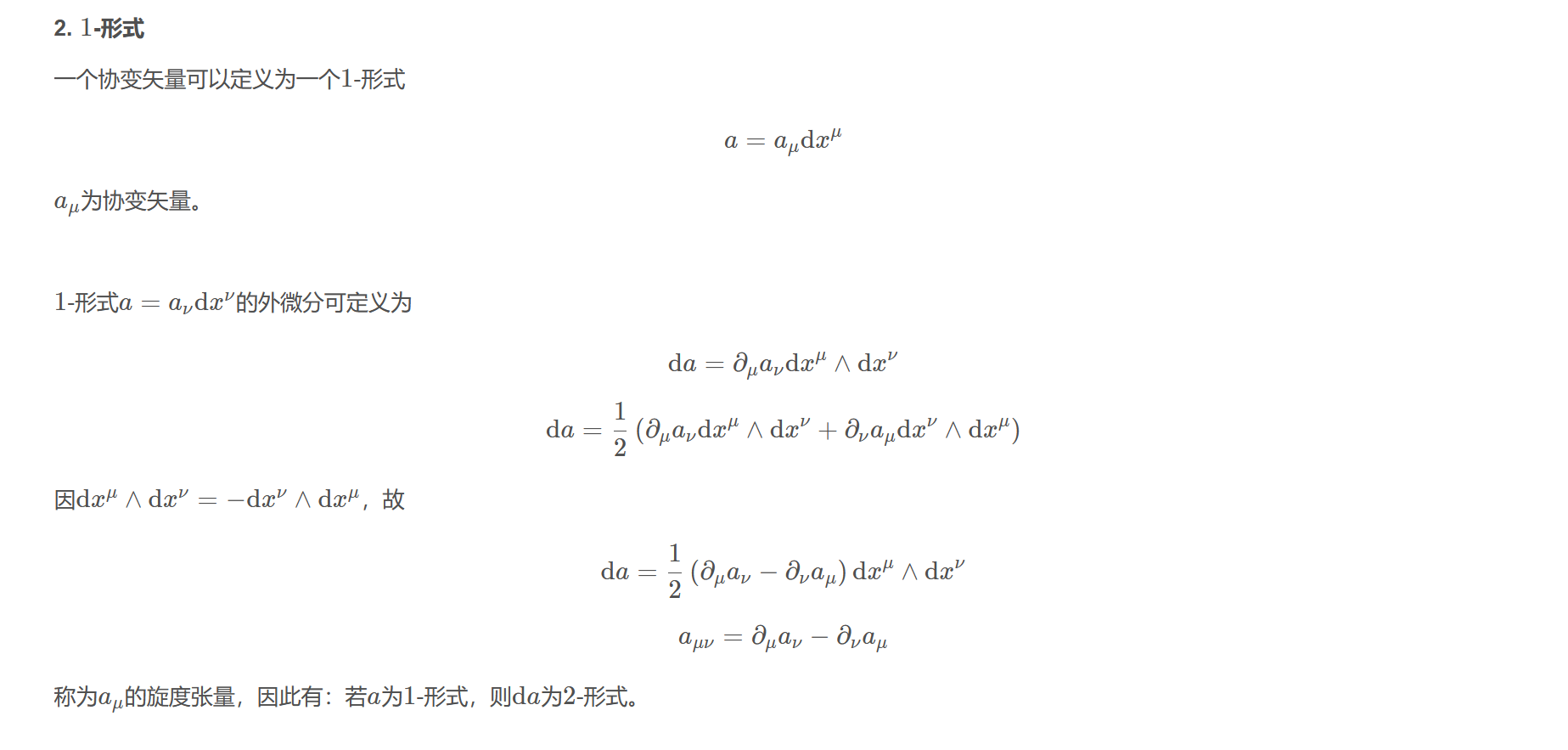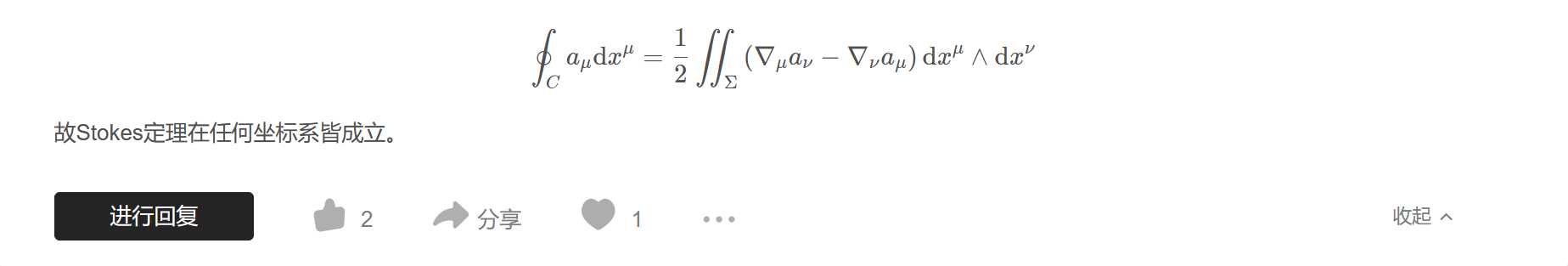物理

【广义相对论速成版】1. Riemann几何 1.8 微分形式与外积

1. $\mathrm{d}x^{\mu}$的外积

矢量$\phi^{\mu},\psi^{\mu}$的内积定义为

$$\braket{\phi|\psi}=g_{\mu\nu}\phi^{\mu}\psi^{\nu}$$

$$\braket{\phi|\phi}=g_{\mu\nu}\phi^{\mu}\phi^{\nu}$$

$\mathrm{d}x^{\mu}$与$\mathrm{d}x^{\nu}$外积定义为

$$\mathrm{d}x^{\mu}\wedge \mathrm{d}x^{\nu}$$

具有反对称性

$$\mathrm{d}x^{\mu}\wedge \mathrm{d}x^{\nu}=-\mathrm{d}x^{\nu}\wedge \mathrm{d}x^{\mu}$$

它是矢量分析中叉乘的提高和推广，$\mathrm{d}x^{\mu_{1}},\mathrm{d}x^{\mu_{2}},\cdots,\mathrm{d}x^{\mu_{n}}$外积的定义为

$$\mathrm{d}x^{\mu_{1}}\wedge\mathrm{d}x^{\mu_{2}}\wedge\cdots\wedge\mathrm{d}x^{\mu_{n}}$$

相邻两个外积是反对称的

$$\mathrm{d}x^{\mu_{p}}\wedge\mathrm{d}x^{\mu_{p+1}}=-\mathrm{d}x^{\mu_{p+1}}\wedge\mathrm{d}x^{\mu_{p}}$$

2. $1$-形式

一个协变矢量可以定义为一个$1$-形式

$$a=a_{\mu}\mathrm{d}x^{\mu}$$

$a_{\mu}$为协变矢量。

$1$-形式$a=a_{\nu}\mathrm{d}x^{\nu}$的外微分可定义为

$$\mathrm{d}a=\partial_{\mu}a_{\nu}\mathrm{d}x^{\mu}\wedge\mathrm{d}x^{\nu}$$

$$\mathrm{d}a=\frac{1}{2}\left(\partial_{\mu}a_{\nu}\mathrm{d}x^{\mu}\wedge\mathrm{d}x^{\nu}+\partial_{\nu}a_{\mu}\mathrm{d}x^{\nu}\wedge\mathrm{d}x^{\mu}\right)$$

因$\mathrm{d}x^{\mu}\wedge \mathrm{d}x^{\nu}=-\mathrm{d}x^{\nu}\wedge \mathrm{d}x^{\mu}$，故

$$\mathrm{d}a=\frac{1}{2}\left(\partial_{\mu}a_{\nu}-\partial_{\nu}a_{\mu}\right)\mathrm{d}x^{\mu}\wedge\mathrm{d}x^{\nu}$$

$$a_{\mu\nu}=\partial_{\mu}a_{\nu}-\partial_{\nu}a_{\mu}$$

称为$a_{\mu}$的旋度张量，因此有：若$a$为$1$-形式，则$\mathrm{d}a$为$2$-形式。

3. $p$-形式

$p$-形式由全反对称协变张量$a_{\mu_{1}\mu_{2}\cdots\mu_{p}}$定义为：

$$a=\frac{1}{p!}a_{\mu_{1}\mu_{2}\cdots\mu_{p}}\mathrm{d}x^{\mu_{1}}\wedge\mathrm{d}x^{\mu_{2}}\wedge\cdots\wedge\mathrm{d}x^{\mu_{p}}$$

$p$-形式$a$的外微分

$$\mathrm{d}a=\frac{1}{p!}\partial_{\mu}a_{\mu_{1}\mu_{2}\cdots\mu_{p}}\mathrm{d}x^{\mu}\wedge\mathrm{d}x^{\mu_{1}}\wedge\mathrm{d}x^{\mu_{2}}\wedge\cdots\wedge\mathrm{d}x^{\mu_{p}}$$

为$(p+1)$-形式。

$p$-形式的二次外微分

$$\mathrm{dd}a=\frac{1}{p!}\partial_{\mu}\partial_{\nu}a_{\mu_{1}\mu_{2}\cdots\mu_{p}}\mathrm{d}x^{\mu}\wedge\mathrm{d}x^{\nu}\wedge\mathrm{d}x^{\mu_{1}}\wedge\mathrm{d}x^{\mu_{2}}\wedge\cdots\wedge\mathrm{d}x^{\mu_{p}}$$

由于$\partial_{\mu}\partial_{\nu}=\partial_{\nu}\partial_{\mu}$，而$\mathrm{d}x^{\mu}\wedge\mathrm{d}x^{\nu}=-\mathrm{d}x^{\nu}\wedge\mathrm{d}x^{\mu}$，故

$$\mathrm{dd}a=0$$

4. 广义协变Stokes定理

因

$$\nabla_{\mu}a_{\nu}=\partial_{\mu}a_{\nu}-\Gamma_{\mu\nu}^{\lambda}a_{\lambda}$$

$$\nabla_{\nu}a_{\mu}=\partial_{\nu}a_{\mu}-\Gamma_{\nu\mu}^{\lambda}a_{\lambda}$$

因

$$\Gamma_{\mu\nu}^{\lambda}=\Gamma_{\nu\mu}^{\lambda}\qquad \text{(无挠)}$$

故

$$\nabla_{\mu}a_{\nu}-\nabla_{\nu}a_{\mu}=\partial_{\mu}a_{\nu}-\partial_{\nu}a_{\mu}$$

一个矢量的旋度一定是个协变旋度。若$T_{\mu\nu}\neq 0$，则协变旋度多了一绕率项，“一个矢量的旋度一定是个协变旋度”对Riemann-Cartan流形就不成立了。

Stokes定理

$$\oint_{C=\partial\Sigma}a_{\mu}\mathrm{d}x^{\mu}=\frac{1}{2}\iint_{\Sigma}\left(\partial_{\mu}a_{\nu}-\partial_{\nu}a_{\mu}\right)\mathrm{d}x^{\mu}\wedge \mathrm{d}x^{\nu}$$

定义$1$-形式

$$a=a_{\mu}\mathrm{d}x^{\mu}$$

则Stokes定理可写成

$$\oint_{\partial\Sigma}a=\iint_{\Sigma}\mathrm{d}a$$

Stokes定理还可有下列协变形式

$$\oint_{C}a_{\mu}\mathrm{d}x^{\mu}=\frac{1}{2}\iint_{\Sigma}\left(\nabla_{\mu}a_{\nu}-\nabla_{\nu}a_{\mu}\right)\mathrm{d}x^{\mu}\wedge \mathrm{d}x^{\nu}$$

故Stokes定理在任何坐标系皆成立。