物理 [TINY NSD]实数集有多少个?
前置知识:Nature佬传奇帖子自然数集是自然数吗?
本帖会在其基础上将数的范围扩展到实数
为表尊重,本帖中涉及Peano公理的内容将会称为Nature公理
别笑,我们高中班上一个姓卞的同学被老师叫上黑板推导阿氏圆,然后我们老师就管阿氏圆叫卞氏圆了
参考资料:程艺《数学分析讲义》第一册、第三册;2025年9月15日与17日程艺在科大授课的内容;来自网上的一些搜索;当然,最重要的,自己的一些思考(程艺书上一堆定理没证)
第一节 自然数
引言:《道德经》曰:“道生一,一生二,二生三,三生万物。”这句话很适合于对后世自然数的定义的理解——如果我们把“道”理解成$\varnothing$的话。Nature公理体系给出了对自然数集性质的一种刻画,但正因为这一特性,其对我等萌新来说并不十分友好。为此,Nature的帖子中提出了更直观的定义,不过冯·诺依曼比Nature抢先了100年(笑)。有了自然数的定义之后,我们又定义了加减乘除四则运算(虽然我们发现此时减法和除法常常没有意义)。然后,利用Nature公理,我们完成了小学二年级就学过的交换律、结合律和分配律的证明。
前置的知识不再重复,我们从最终Nature留下的自然数的定义开始看:
${0=\varnothing}$
${1=\lbrace \varnothing \rbrace=\lbrace 0 \rbrace}$
${2=\lbrace \varnothing, \lbrace \varnothing \rbrace\rbrace=\lbrace 0, 1 \rbrace}$
……
当然,我们看上面的内容,自然能理解自然数的概念,但是这样的描述还是不严谨的,毕竟,我们只列出了0,1,2,后面的数呢?
通过观察,我们发现自然数集的定义中最核心的一点:
①${若a \in \mathbb{N},则a \cup \lbrace a \rbrace \in \mathbb{N}}$。
但是只有这一句核心是远远不够的。比如说,空集显然满足①,但我们肯定不能说空集是自然数集。此外,集合${\lbrace 1, 2, ... \rbrace}$也满足条件,但我们同样不能说是自然数集。所以,我们还需要补充其他的内容。
②${\varnothing \in \mathbb{N}}$。
如此就回避了上面的一系列问题。不过,还是不够。所有的自然数都在里面了,但如果我们在里面塞一个奇怪的东西呢?
比如,如果我们把一个苹果放在$\mathbb{N}$里面,会发生什么?
我们会发现,这个苹果会给自然数集添加无穷多的新元素,但是并不会与上述两条构成矛盾!
可是这个苹果是怎么来的?还不是我们硬塞的!没有实际意义!
所以,我们可以再补一条:
③若${a \in \mathbb{N}且a \neq \varnothing}$,则${\exists b \in \mathbb{N},a=b \cup \lbrace b \rbrace}$。
这样我们确保了,除了一开始的$\varnothing$,我们没办法把任何其他奇奇怪怪的东西硬塞到自然数集里面。
所以,我们就得到了自然数集的一种刻画:
①${若a \in \mathbb{N},则a \cup \lbrace a \rbrace \in \mathbb{N}}$;
②${\varnothing \in \mathbb{N}}$;
③若${a \in \mathbb{N}且a \neq \varnothing}$,则${\exists b \in \mathbb{N},a=b \cup \lbrace b \rbrace}$。
这在论坛是Nature的伟大发现,不过正如本章引言说的,被冯·诺伊曼抢先了。大家知道冯·诺伊曼或许仅仅是因为计算机,然而这一对自然数的刻画也是他的贡献。
满意了吗?还是没有!因为我们注意到,里面出现了${a \cup \lbrace a \rbrace}$这样的东西,这是啥玩意?
我们发现,这样的规定好像不是必须的!换成别的奇奇怪怪的构造,除了一些微调之外,似乎没有任何影响!
那我们为啥不用更加一般的表示方法?
所以,对①②两条,我们可以有更一般的表达:
1)${0 \in \mathbb{N}}$;
2)${若a \in \mathbb{N}}$,则我们可以定义$a$的后继数${S(a)}$,使${S(a)\in \mathbb{N}}$。
不过我们发现,这样就不能直接套用③来防止“硬塞”的现象了。
为什么呢?考虑这样的定义:如果我们规定${S(0)=0}$,那么${\lbrace 0 \rbrace}$也成为自然数集了,这显然不对!
所以,对于0,我们可以加特殊的限定:
3)${\forall a \in \mathbb{N},S(a)\neq 0}$。
但是类似的问题依然存在。如果我们令${S(0)=S(1)=1}$,那么集合${\lbrace 0, 1 \rbrace}$也符合上述三条,但同样不是自然数集。
为此,除了3)之外,我们还需要有一条4):
4)${\forall a, b \in \mathbb{N},S(a)=S(b)当且仅当a=b}$。
其实3)与4)本质接近,都是为了避免出现循环。只不过由于0的特殊性,我们需要把3)从4)中独立出来,这样才算严谨。
看起来,我们已经修补完了把②一般化带来的问题。不过当我们准备把③抄下来的时候,却发现,还是不对!
比如,我们总可以定义${a_0 \ne 0,且S(a_n)=a_{S(n)} \ne S(n)}$。
同时,我们又定义${b_0=a_0,且S(b_{S(n)})=b_n}$。
现在,如此定义自然数集${\mathbb{N}}$:
①${0 \in \mathbb{N}}$,${a_0 \in \mathbb{N}}$;
②${若n \in \mathbb{N},则S(n) \in \mathbb{N}}$;
③${若b_n \in \mathbb{N},则b_{S(n)} \in \mathbb{N}}$。
我们惊奇地发现,这样定义出来的自然数集居然不违背1)~4),并且除了0以外,每个数都是别的数的后继!
问题出在哪里呢?还是拿苹果打比方。
如果说一个苹果${=a \cup \lbrace a \rbrace}$,这显然是荒谬的;
但如果说一个苹果是别的东西的后继,我们居然找不出任何问题!
所以归根到底,原始③的调整还是跟②的一般化挂钩。
于是,为了更进一步避免任何混进自然数里的“杂质”,我们可以使用一个更一般的限制:
5)若${S \subseteq \mathbb{N}}$,且${S}$满足性质1)2),那么${S=\mathbb{N}}$。
这样就可以把其他杂质的路全都锁死了。
我们前面一直用到“杂质”一词,但始终没有明确的定义,这点很难深究,因为我们的工具太过稀少,很多东西没法精确定义。
但可以肯定的是,现在的自然数集中不会出现一些莫名其妙的“苹果”,
否则把它们都去掉,只剩下0,S(0),...之后,得到的集合仍满足1)2),这会与5)矛盾。
就这样,我们得到了用于规范自然数的五条公理。
实际上,这也正是数学家Peano所作出的发现,甚至比冯·诺伊曼还要早30余年。1)~5)一般也被称作Peano公理,不过正如前面提到的,我们会称它为Nature公理。
自然数有了,接下来我们需要什么?
两件事:一,大于和小于,我们管这叫序关系;二,加减乘除,我们管这叫四则运算。
直接从大小于入手似乎有些困难,我们先归纳定义加法:
①${\forall n \in \mathbb{N},n+0=n}$;
②${\forall a, b \in \mathbb{N}, a+S(b)=S(a+b)}$。
有了加法,我们就可以着手证明我们熟悉的结合律和交换律了。
等一下!为什么结合律在前,交换律在后?
看看证明过程就知道了。
首先,我们要引入一个重要的工具:数学归纳法。
若关于自然数的命题${P(n)}$满足以下两个条件:
1)${P(0)}$为真;
2)若${P(n)}$为真,则${P(S(n))}$为真。
则${\forall n \in \mathbb{N}, P(n)}$为真。
证明:记${S=\lbrace n \in \mathbb{N}|P(n)为真\rbrace}$。
则${S \subseteq \mathbb{N}}$, ${0 \in S}$, 且若${n \in S,总有S(n) \in S}$。
由Nature第五公理,${S=\mathbb{N}}$,即${\forall n \in \mathbb{N}}$,${P(n)}$为真。
证毕。
由此,我们可以开始结合律的证明。
结合律:${\forall a, b, c \in \mathbb{N},a+(b+c)=(a+b)+c}$。
证明:当${c=0}$时,${a+(b+c)=a+(b+0)=a+b=(a+b)+0=(a+b)+c}$,成立。
假设${c=k}$时成立,考虑${c=S(k)}$:
${a+(b+S(k))=a+S(b+k)=S(a+(b+k))=S((a+b)+k)=(a+b)+S(k)}$,成立。
由数学归纳法,${\forall a, b, c \in \mathbb{N}}$,${a+(b+c)=(a+b)+c}$。证毕。
交换律的证明略为复杂,需要用到三次数学归纳法:
交换律:${\forall a, b \in \mathbb{N},a+b=b+a}$。
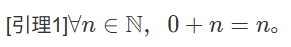 (人机违禁词判定射皇了)
(人机违禁词判定射皇了)
证明:当${n=0}$时结论显然。
假设${n=k}$成立,则${0+S(k)=S(0+k)=S(k)=S(k)}$。
由数学归纳法,引理1得证。
[引理2]${\forall a, b \in \mathbb{N},a+S(b)=S(a)+b}$。
证明:${b=0}$时,${a+S(b)=a+S(0)=S(a+0)=S(a)=S(a)+0}$,成立。
假设${b=k}$时成立,则${a+S(S(k))=S(a+S(k))=S(S(a)+k)=S(a)+S(k)}$,成立。
由数学归纳法,引理2得证。
回到原题。当${b=0}$时,由引理1,总有${a+0=a=0+a}$,成立。
假设${b=k}$时成立,则${a+S(k)=S(a+k)=S(k+a)=k+S(a)=S(k)+a}$(由引理2)。
由数学归纳法,${\forall a, b \in \mathbb{N}}$,加法交换律成立。证毕。
此外,我们还需要说明加法的一条重要性质(消去律):
${a=b}$当且仅当${a+c=b+c}$。
证明:必要性显然。下只需证充分性。
当${c=0}$时显然成立。
假设${c=k}$时成立,考虑${a+S(k)=b+S(k)}$:
由加法的定义与Nature第四公理,${S(a+k)=a+S(k)=b+S(k)=S(b+k)}$,从而${a+k=b+k}$。
由归纳假设,必有${a=b}$。
综上,若${a+c=b+c}$,则${a=b}$,充分性证毕。
为什么说这条性质很重要呢?因为定义减法时需要用到。
我们以减法作为加法的逆运算,前提是得到的结果是唯一的。而由上面的性质,可以得到一个推论:
${\forall a, b \in \mathbb{N}}$,至多存在一个自然数$k$,使得${a+k=b}$。
证明:反证法,假设${\exists k_1, k_2 \in \mathbb{N}}$且${k_1\neq k_2}$,使得${a+k_1=a+k_2=b}$:
由加法交换律,${k_1+a=a+k_1=a+k_2=k_2+a}$,
由上述性质即得${k_1=k_2}$,矛盾!故原命题得证。
据此,我们引入减法的定义:
${对自然数a, b,若\exists k \in\mathbb{N}使a+k=b,则称a \leq b,并记k=b-a}$。
序的定义也在这里完成了。
我们先研究序,再研究加减混合运算:
性质:自然数集上的序${\leq}$是一种良序关系,即满足以下四点:
1)${对a, b \in \mathbb{N},若a \leq b且b \leq a,则a=b}$;
2)${对a, b, c \in \mathbb{N},若a \leq b且b \leq c,则a\leq c}$;
3)${\forall a, b \in \mathbb{N},要么a \leq b,要么b \leq a}$;
4)${\forall S \subseteq \mathbb{N}且S \neq \varnothing,\exists a \in S, \forall b \in S,a \leq b}$。
证明:1)[引理1]${\forall n\in \mathbb{N}且n \neq 0,\exists m \in \mathbb{N},n=S(m)}$。
证明:定义集合${S=\lbrace n \in \mathbb{N}|n=0或\exists m\in \mathbb{N}, n=S(m) \rbrace}$,
则${0 \in S}$,且若${k \in S, S(k) \in S}$。
由Nature第五公理,必有${S=\mathbb{N}}$,
即${\forall n \in \mathbb{N},n=0或\exists m \in \mathbb{N}, n=S(m) }$。证毕。
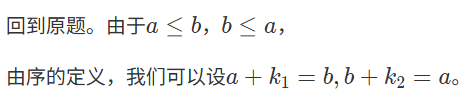
则${a=b+k_2=(a+k_1)+k_2=a+(k_1+k_2)=(k_1+k_2)+a}$。
又${a=0+a}$,故由消去律,${k_1+k_2=0}$。
假设${k_2 \neq 0}$,则${\exists m \in \mathbb{N},k_2=S(m)}$,
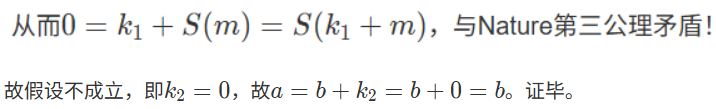
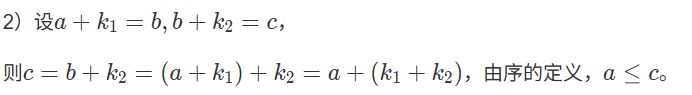
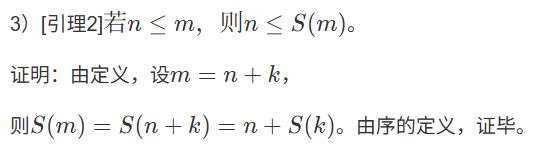
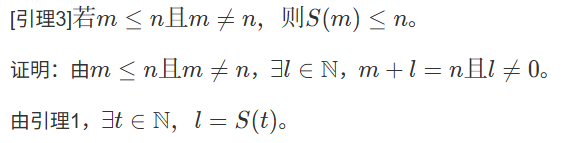
则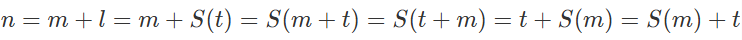 。
。