数学

关于勾股定理

前言：没有前言！(直接进入正题)

        勾股定理是描述直角三角形三条边之间关系的一个基本定理。

$$\huge{核心内容：}$

        在一个直角三角形中：

1.  两条较短的边称为 “勾” 和 “股”（通常用字母 “$a$” 和 “$b$” 表示，说白了就是两直角边）。

2.  最长的那条边（即直角所对的边）称为 “弦” 或 “斜边”（通常用字母 “$c$” 表示，说白了就是斜边）。

3.  定理表述：两条直角边的平方和等于斜边的平方(具体请看第四条)。

4.  数学公式：<$a^2+b^2=c^2$> 直角位于 “$a$” 和 “$b$” 相交的顶点。斜边 “$c$” 与直角相对。

$$\huge{历史与命名：}$

        这个定理在中国古代数学著作《周髀算经》中就有记载，并由三国时期的数学家赵爽用“弦图”给出了证明。

        在中国，它被称为“勾股定理”或“商高定理”。

        在西方，这个定理最早由古希腊数学家毕达哥拉斯（Pythagoras）或其学派发现并证明，因此被称为“毕达哥拉斯定理”（Pythagorean Theorem）。

$$\huge{证明方法：}$

        勾股定理有非常多的证明方法（据说超过400种😯）。

        以下是其中一种直观且经典的证明（类似于赵爽的弦图）如图：

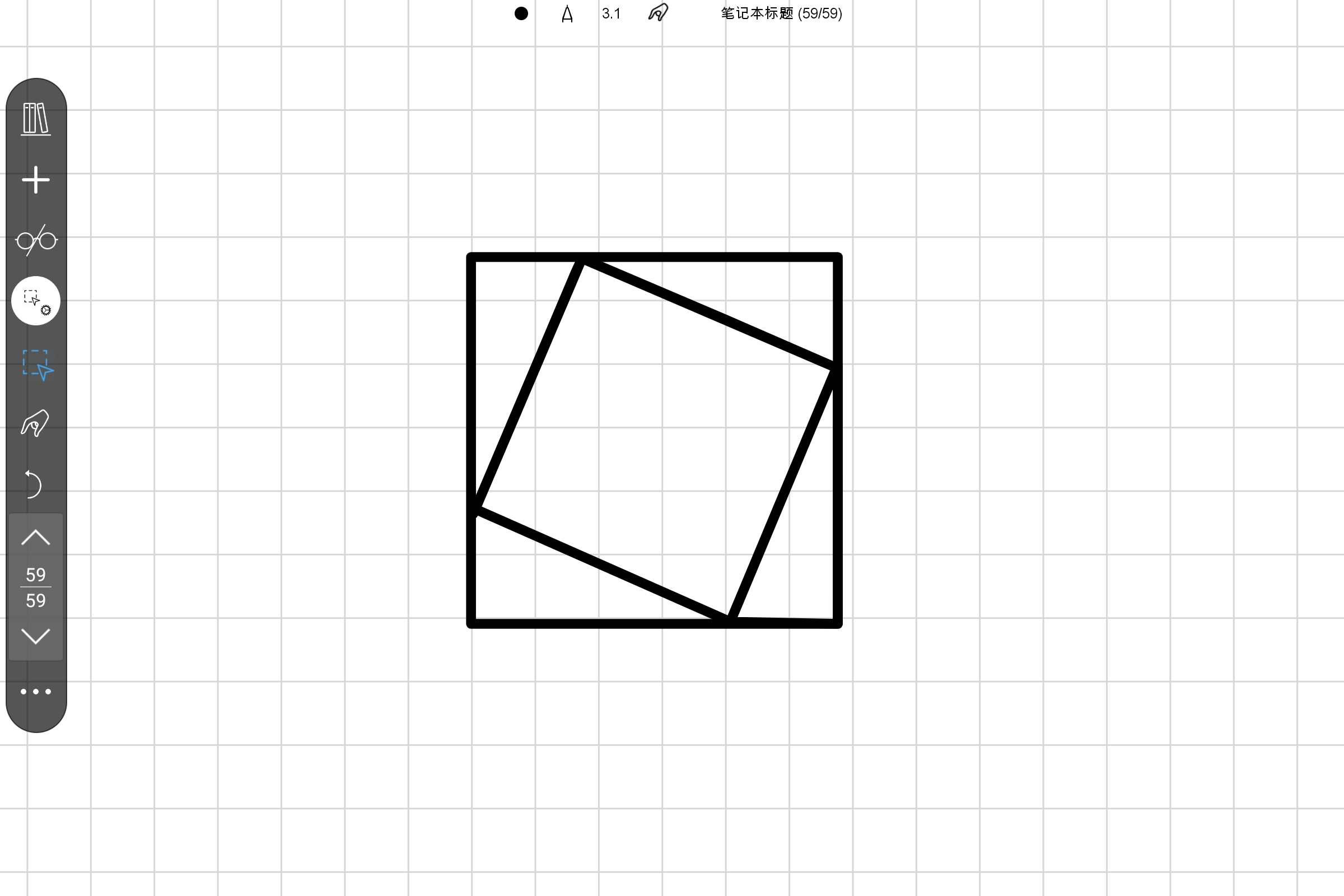
1.  构造：取四个完全相同的直角三角形（直角边为 “$a$” 和 “$b$”，斜边为 “$c$”）。使它们的直角位于外围，斜边 “$c$” 朝向内部。

2.  形成大正方形： 这四个直角三角形恰好拼成了一个大正方形。这个大正方形的边长是多少🤔？观察大正方形的边：它由一条直角边 “$a$” 和另一条直角边 “$b$” 组成。所以，大正方形的边长是 “$(a+b)$”。因此，大正方形的面积是 “$(a+b)^2$”。

3.  内部小正方形： 同时，四个直角三角形的斜边 “$c$” 在中间围出了一个小正方形。这个小正方形的边长就是 “$c$”。因此，小正方形的面积是 “$c^2$”。

4.  面积关系：大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积。大正方形面积 = “$(a+b)^2$”，一个小直角三角形面积 = “$\frac{1}{2}×a ×b$”，四个小直角三角形面积 = “$4×\frac{1}{2}×a×b=2ab$”中间小正方形面积 = “$c^2$” 所以：“$(a+b)^2=2ab+c^2$”。

5.  展开化简：展开左边：“$(a+b)^2=a^2+2ab+b^2$”代入等式：“$a^2+2ab+b^2=2ab+c^2$”

6.  得出结论：两边同时减去 “$2ab$”：“$a^2+b^2=c^2$”

$$\huge{应用：}$

        勾股定理是几何学中最基础、最重要的定理之一，应用极其广泛，例如：1.  求边长： 已知直角三角形的任意两边，求第三边(用于秒杀数学题)。例：已知 “$a=3, b=4$”，求斜边 “$c$”： “$c^2=3^2+4^2=9+16=25$”得出“$c=5$” 2. 验证直角：如果一个三角形的三边满足 “$a^2+b^2=c^2$”（其中 “$c$” 是最长边），那么这个三角形一定是直角三角形（勾股定理的逆定理）。例：边长$3、4、5$推得“$3^2+4^2=9+16=25=5^2$”，所以是直角三角形。3.  测量与工程：计算距离（如地图上两点间的直线距离）、高度（如利用影子测楼高）、设计结构（确保角度是直角）。4.  数学基础：它是三角函数、解析几何（两点间距离公式）、向量模长计算等许多高等数学和物理概念的基础。5.  导航：计算位置和方向。重要概念(重要事情说三遍)：只适用于直角三角形！只适用于直角三角形！只适用于直角三角形！若对于锐角三角形或钝角三角形，则不满足 “$a^2+b^2=c^2$”。斜边（c）是最长边：它总是直角所对应的边。逆定理成立：如果三边满足 “$a^2+b^2=c^2$”（“$c$”最大），则它是以 “$c$”为斜边的直角三角形。

$$\huge{总结：}$

        勾股定理 ($a^2+b^2=c^2$) 揭示了直角三角形三边之间简洁而深刻的平方关系。它是数学史上最著名的定理之一，是连接几何与代数的重要桥梁，在理论研究和实际应用中都具有不可替代的地位。无论是古代的测量、建筑，还是现代的科学技术（如GPS定位、计算机图形学），都离不开它的身影哦😎！