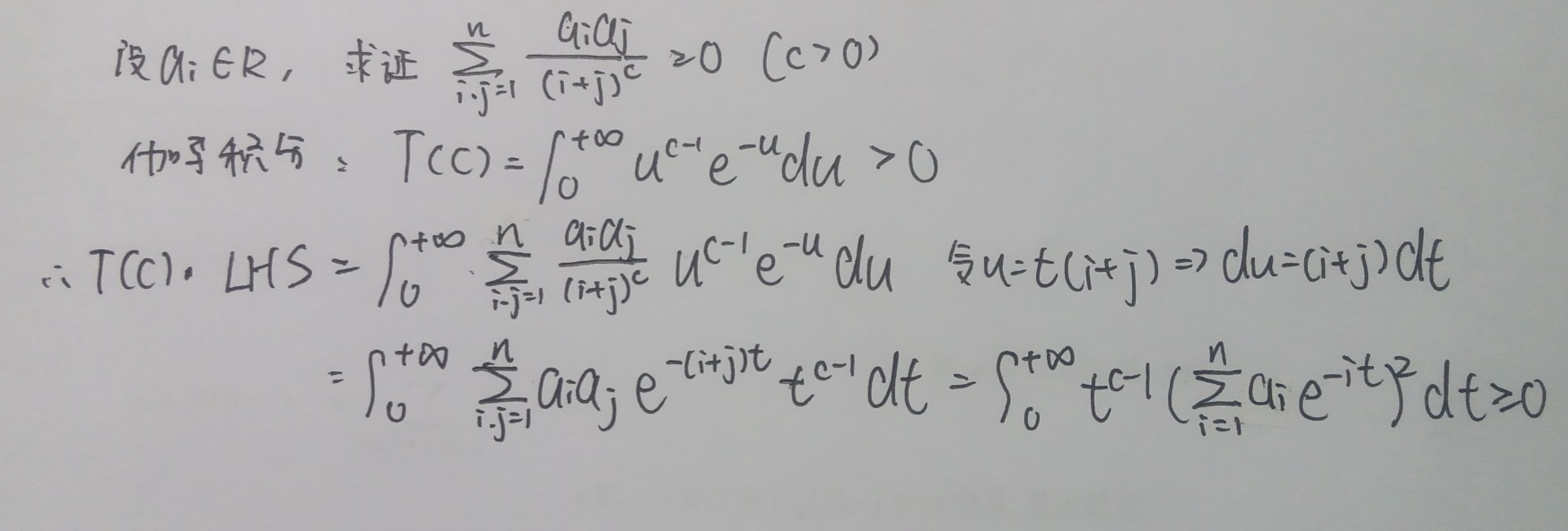物理

Γ(x)伽玛函数

大家都知道n！阶乘，阶乘是一个非负整数n的乘积，所有小于等于n的正整数相乘。记作n!。例如，5! = 5 × 4 × 3 × 2 × 1 = 120。可是真的只有非负正整数有阶乘吗？并不是，当我们在数学函数绘制软件desmos上输入f(x)=x!时，便会出现一个形状奇怪的函数图像，而且并不是只有在x为整数时y才有图像。可是怎么计算非整数的阶乘呢？这就需要伽玛函数了，已知Γ(x)=$\Huge{∫_0^{\infty}t^{x-1}e^{-t}dt}$,Γ(x+1)=xΓ(x)=x!😎,这时候又有人问了伽玛函数的上限是无穷啊，该怎么计算呢？🤔我们可以把伽玛函数化成有限区间函数，令$\color{blue}e^{-t}$=u 经过一系列计算，

这个函数就变成了$\color{red}∫_0^1(-ln(u))^{x-1}du$这下我们只需要积个分就可以了，当然积分的时候要先把x带入进去。

验证：2!=Γ(3)=2Γ(2)=2*$\color{cyan}∫_0^1(-ln(u))du$=2*(1-1*ln1)=2对了😎，备注:因为原式中次数(2-1)=1任何数的一次方都得原数，所以省略不写。

还有一个，我发现在运算的时候可能会让函数出现虚数，这该怎么办呢，我把函数又弄了一下

变成了这样：$\Huge{∫_0^1(ln (1/u))^{x-1}du}$

若有错误或可改进的方案欢迎留言。

哦对了，如果你觉得微积分对于你实在看不懂的话，之后我更如何不用微积分求阶乘值。$\sout{其实是懒癌发作了，不想写(更)}$