物理 狄利克雷函数与勒贝格积分
提示：本贴已完结，个人认为是比较易懂的帖子，适合入门，开服老玩家请移步专业教材😇
由于 @尊嘟假嘟0.o 跑路了，所以让我帮忙写👁️👄👁️
学习建议：掌握数学分析，尤其是实数的完备性以及第一章的1、2节，如果只是为了理解思想只要有一点点微积分基础即可
直入正题
狄利克雷函数是这样一个函数：$D(x)=\begin{cases}1,&x\text{为有理数}\\0,&x\text{为无理数}\end{cases}$
我们都知道这个函数是黎曼不可积的一个函数，例如要在区间$[0,1]$积分
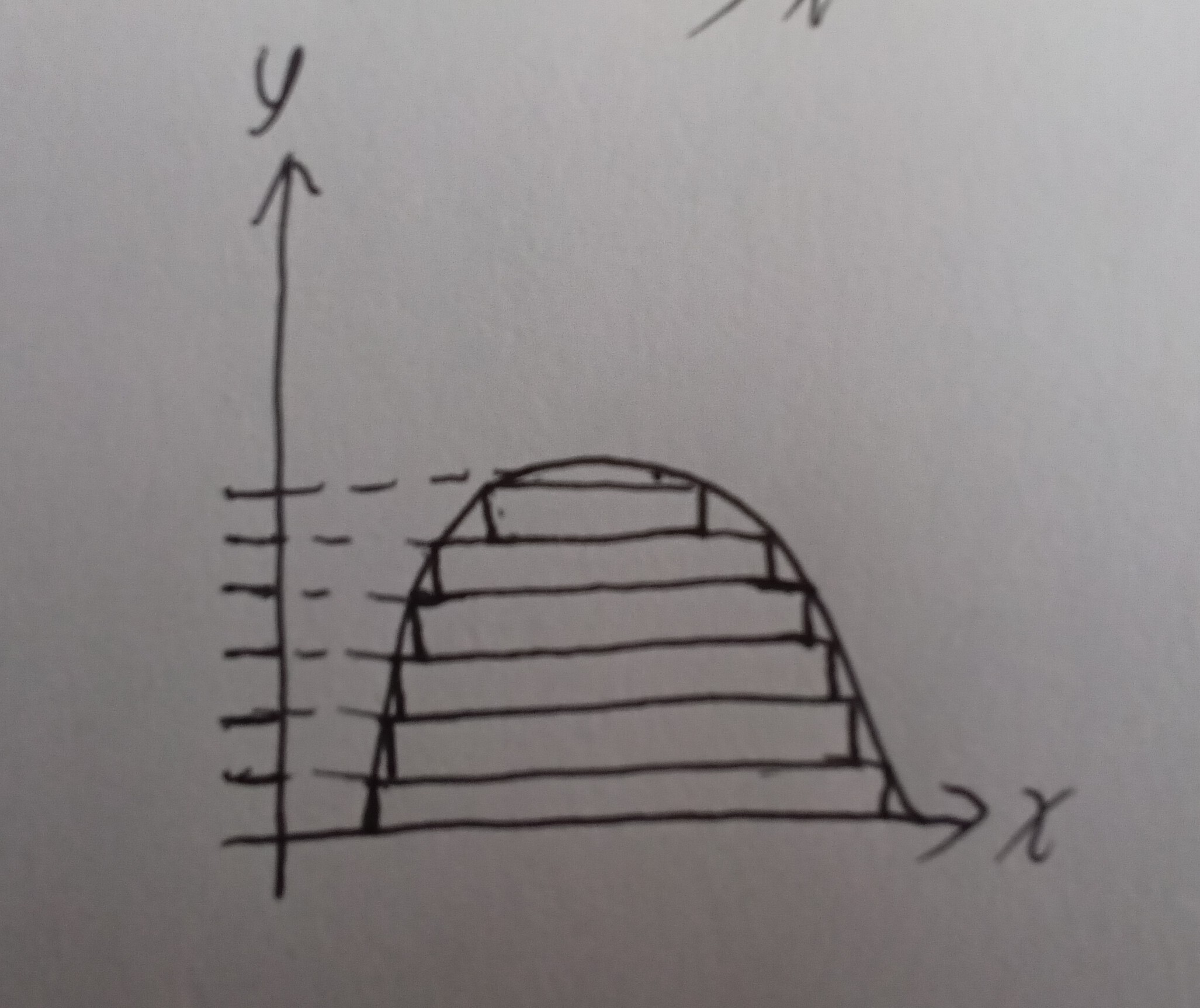
首先在$[0,1]$插入分点形成子区间，再取点求和
由于有理数的稠密性，所以在任何一个区间里都能取到有理数，如果取到的点$ξ_k$都是有理数，那么所有$D(ξ_k)=1$，黎曼和$\sum 1·Δx_k=1$
同理，由于无理数的稠密性又可以得到黎曼和为0
因此通过改变取点的方式黎曼和就可以在0和1间震荡，无法逼近唯一的极限，因此黎曼函数失效
这个时候需要一种新的积分方法：勒贝格积分
来用一个肥肠通俗易懂的例子看一下勒贝格积分与黎曼积分的区别
你有一大堆面值不同的钞票，有一块的，五块的，十块的，三十块的……
用黎曼的方法是这样数的：第一张，一块，记下，第二张五块，累加，第三张30块，累加……直到最后一张
这里关系的是数钱的顺序，如果钞票被打乱，过程会变，但是结果不会
在数学上这是黎曼积分，把x轴分成细小的区间，在每个区间上取函数值(即钞票面积)乘上区间宽度(钞票的厚度，这里每张厚度一样)，再求和，它关心的是在$\LARGE{定义域}$上切分
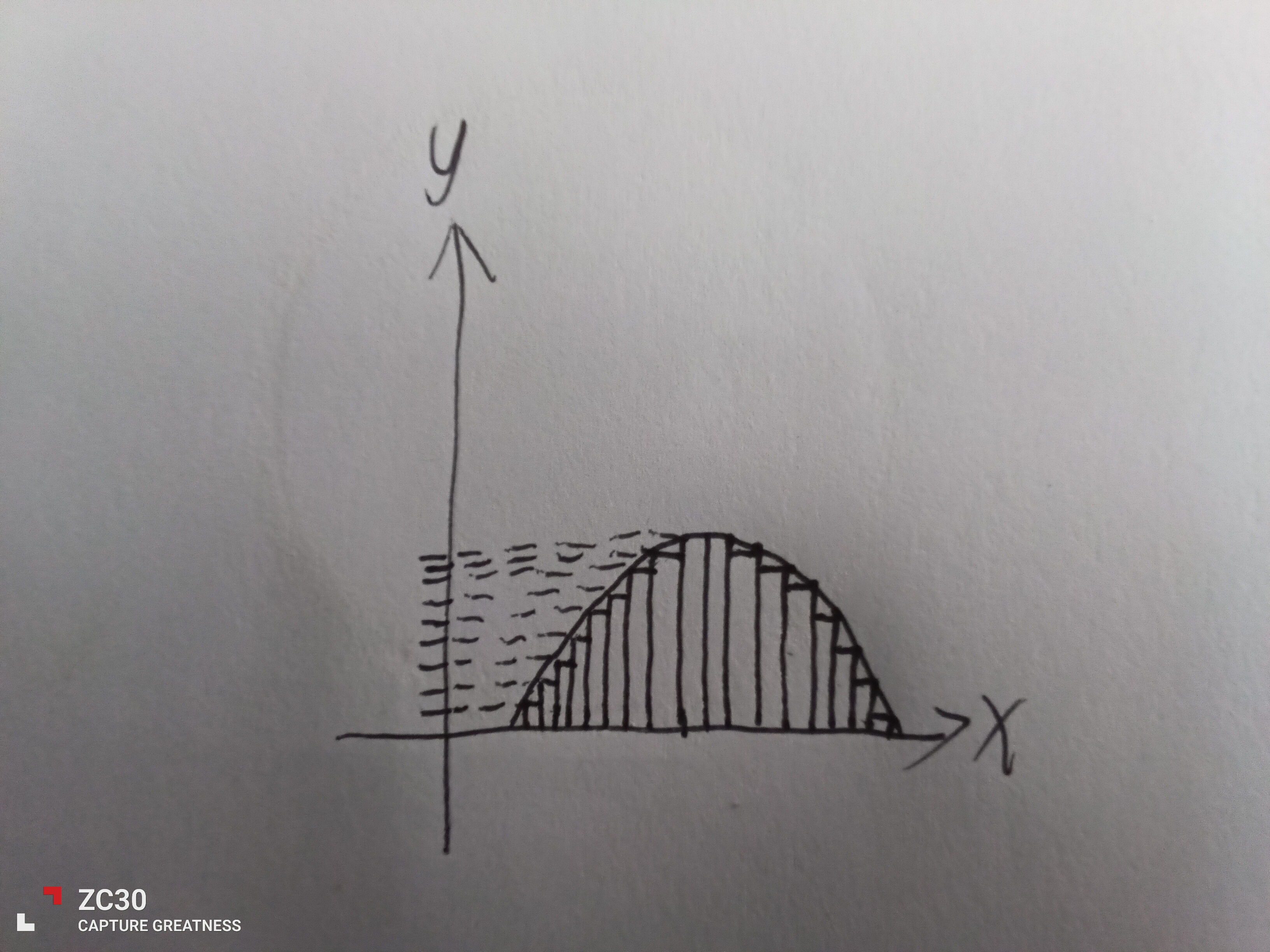
接下来用新的方法，勒贝格的方法：先把所有1块的挑出来，一共10张，共10块，再挑出来5块的，5张，一共25块……最后把每个类别的金额加起来
你不关心钞票原本的顺序，只关心每种面值有多少张，他关心的是$\LARGE{值域}$的划分
因此黎曼积分的核心思想是 分割定义域→近似求高→求和
勒贝格的核心思想是 分割值域→测量‘‘底’’的大小→求和
但这里引出一个关键问题：对于‘‘底’’的大小，我们以前用区间的长度，但现在的‘‘底’’可能是一堆点集，我们如何测量它们的大小？
这时就要引出一个重要概念：勒贝格测度
我们希望给数轴、平面、空间上的集合$E$分配一个非负实数$m(E)$，称之为它的测度，用来表示它的‘‘长度’’、‘‘面积’’、‘‘体积’’，这个定义必须满足两个要求：
兼容性：对于区间$[a,b]$必须有$m([a,b])=b-a$
可数可加性：如果有一系列$\Large{互不相交}$的集合$E_1,E_2,E_3,$…，则有$m\left(\bigcup_{k=1}^{∞}E_k\right)=\sum_{k=1}^{∞}m(E_k)$
很显然，这个东西放在这很阴，所以还是翻译成人类语言：如果有一系列互不相交的集合$E_1,E_2,E_3,$…，那么它们之并的测度必须等于它们各自测度的和
这就是勒贝格测度区别于古典长度最核心的性质
恩对，上面说的貌似都是希望，需要实现一下：
如何测量一个任意集合$E$的大小？勒贝格的想法是‘‘从外部覆盖’’，因此也就有了勒贝格外测度
为了理解这个我们再举一个例子
企鹅在他的作业上撒了半瓶墨水，他想测量墨水覆盖的面积，于是他用透明网格纸盖在上面，数了数被墨水碰到的格子，面积一定要比真是面积大，然后他换了一个格子更细密的透明网格纸重复过程
当格子的尺寸无限缩小时，格子的面积就是墨水的面积
这里给出勒贝格外测度的定义：$m^{*}(E)=\inf\left\{\sum_{k=1}^∞\ell(I_k):E⊆\bigcup_{k=1}^∞I_k\right\}$
很显然，这个也很阴，解读一下：用可数无穷多个开区间$I_k$覆盖集合$E$，所有这些可能覆盖的长度之和$\sum\ell(I_k)$构成一个集合，这个集合的下确界就是集合$E$的勒贝格外测度
我们举些例子：$m^*([1,2])=1$，因为$2-1=1$，$m^*({1,2,3})=0$，因为每个点的测度为0，三个点是3×0
我们在集合论中学过有理数集$\mathbb{Q}$是可数集，所以测度为0
这时候我们发现有一些特殊集合的外测度并不满足可数可加性，而是只能满足这样的次可数可加性(例如Vitali集)：$m\left(\bigcup_{k=1}^{∞}E_k\right)≤\sum_{k=1}^{∞}m(E_k)$
所以我们要挑选出那些满足条件的集合，也就是可测集
定义：如果对于$\Large{任意}$测试集$A⊂\mathbb{R}$都有：$m^*(A)=m^*(A∩E)+m^*(A∩E^C)$，则称集合$E$是勒贝格可测的
也就是说集合$E$的边界必须要足够光滑，能将任何集合$A$分成在$E$里和在$E$外两部分，且这两部分的尺寸和等于$A$的外尺寸
所有的可测集构成一个σ-代数，对于可测集$E$，其外测度$m^*(E)$就称为它的勒贝格测度，记为$m(E)$
这个时候我们已经学习了勒贝格测度，也就可以计算一开始的问题
聪明的你发现要计算狄利克雷函数在$[0,1]$区间的积分就是计算$m^*(\mathbb{Q}∩[0,1])·1$，很显然，这个值为0
也就是说狄利克雷函数在$[0,1]$区间的积分值为0
当然这个是最显而易见的一个函数积分，我们需要计算更一般的函数——简单函数，我们有这样一个定义：
$s(x)=\sum^n_{i=1}c_i·χ_{E_i}(x)$
其中$E_i$是互不相交的可测集，$χ_{E_i}(x)$是示性函数，意思是若$x∈E_i$函数值为1，否则为0，上面说的狄利克雷函数就是典型的示性函数，$c_i$是每个可测集$E_i$的系数
这个函数整体呈阶梯状，有一节一节的，应该不难理解，嗯对。
$\sout{不难看出}$这个函数的勒贝格积分是这样定义的：$∫sdm=\sum^n_{i=1}c_i·m(E_i)$
这个时候我们把狄利克雷函数带进去再算一次，这里的$n=1$，$c_1=1$，$E_1$即集合$\mathbb{Q}∩[0,1]$，易得积分值为0
因为本贴名字是勒贝格积分，所以只更到这里，后续一般函数的勒贝格积分，可测函数，$L^p$空间等知识都没有讲到，想要深入了解实变函数可以自行查阅资料
完结撒花(^_-)-☆
(其实是懒癌发作不想更了(大声蛐蛐
共3条回复
时间正序
饼ヾ芒(-5
1月前
紧急通知！！！
不要把勒贝格积分理解成这样分割！！！
这里的分割值域不是横向积分，依然是纵向的，当时我就是这样误解的，后面才清楚
正确积分形式是这样的
注意哈，这里的分割是无穷小的，每一份是相当的，图不规范，理解大致意思就行😥
2条评论
- 1
即未用户9223
1月前
能不能求一下爆米花函数的勒贝格积分？
爆米花函数：(在无理点连续，在有理点不连续)
$f(x)=\begin{cases}\frac{1}{q}~~~x=\frac{p}{q},p,q∈\mathbb{N}^{*},(p,q)=1\\0~~~x∉\mathbb{Q}\\1~~~x=0\end{cases}$
7条评论
饼ヾ芒(-5
1月前
这个自由基佬好像讲过
简单一点就是因为函数取非0值只在$\mathbb{Q}$上，$\mathbb{Q}$测度为0，几乎处处为0的函数勒贝格积分也为0
爆米花函数貌似就是数分里那个黎曼函数(？)
即未用户9223 回复 饼ヾ芒(-5
1月前
应该不是吧？
Riemann函数：
$\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s},s{\gt}1$
饼ヾ芒(-5 回复 即未用户9223
1月前
这个好像是Riemann-Zeta函数👁️👄👁️
数学分析第一章第三节好像说过Riemann函数
即未用户9223 回复 饼ヾ芒(-5
1月前
这两个黎曼函数不是一个？
饼ヾ芒(-5
1月前
好像不是一个东西👁️👄👁️
数分上是这样写的(好像和爆米花函数不太像？)
即未用户9223 回复 饼ヾ芒(-5
1月前
有可能是我记错了，好像就是这个函数
饼ヾ芒(-5 回复 即未用户9223
1月前
哦哦，彳亍，你写的那个函数勒贝格积分也是0，证法差不多🌚
