物理

2025USTCMATHEntrance（真题回忆版）

17：00考完，19：00考物理，智英晚饭都不吃了来抢着给你们发题，快感谢我

不过不妨碍我考场上又唐没边算错一堆（汗）

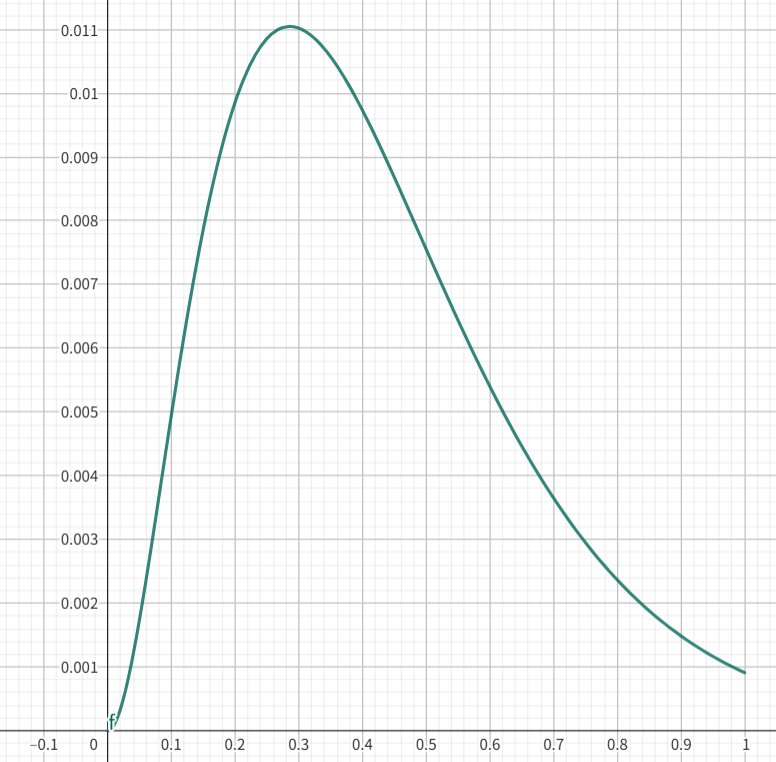
1.下图为${f(x)=x^ae^{-bx}(0 \lt x \lt 1)}$的图像，其中${a, b \in \lbrace 1, 2, 3, ..., 9 \rbrace}$，则${a=\_\_\_\_\_\_\_\_}$。

2.将${\sqrt{2}, e^\frac{1}{\pi}, e^\frac{1}{e}, \pi^\frac{1}{e}}$按从小到大排序：${\_\_\_\_\_\_\_\_}$。

3.若方程${2\sin x=x+c}$在${(0, 2\pi)}$上有且只有一根，则$c$的取值范围是${\_\_\_\_\_\_\_\_}$。

4.若复数$z$满足${|z|=|z+1-i|}$，则${z^2=x+yi}$在复平面上的轨迹是${\_\_\_\_\_\_\_\_}$。

5.椭圆${x^2+2xy+3y^2=4}$的长轴方程为${\_\_\_\_\_\_\_\_}$。

6.${\sum_{k=1}^n{k^5}=\_\_\_\_\_\_\_\_}$。

7.已知无盖长方体容器的表面积为$1$，则其容积最大值为${\_\_\_\_\_\_\_\_}$。

8.Fibonacci数列的前2025项有${\_\_\_\_\_\_\_\_}$个数能被9整除。

9.已知${\triangle ABC}$中，$D$，$E$，$F$分别为${BC, AC, AB}$三边上的点，用${a, b, c}$表示${|DE|+|EF|+|DF|}$的最小值。

10.四面体ABCD中，记${\ell_A}$过点$A$且垂直于平面$BCD$，${\ell_B}$过点$B$且垂直于平面$ACD$，${\ell_C}$过点$C$且垂直于平面$ABD$，${\ell_D}$过点$D$且垂直于平面$ABC$，求证：若${AB \perp CD}$且${AC \perp BD}$，则${\ell_A, \ell_B, \ell_C, \ell_D}$四线共点。

11.求证：${\sum_{i=1}^{2025}\sqrt{a_i^2+b_i^2} \ge \sqrt{(\sum_{i=1}^{2025}a_i)^2+(\sum_{i=1}^{2025}b_i)^2}}$，并给出取等条件。

12.是否存在独立的随机变量${X, Y}$，其分布列相同，且${P(X+Y=k)=\frac{\min \lbrace k, 14-k \rbrace}{47}(k \in \lbrace 2, 3, ..., 12 \rbrace)}$？并说明理由。