物理

天文竞赛专题----红移

对天文竞赛生来说，只需要了解哈勃定律$v=HD$以及红移的波长公式$z = \frac{\lambda - \lambda_0}{\lambda_0}$就够了，不过作为专题，我们还需要再深入一下。

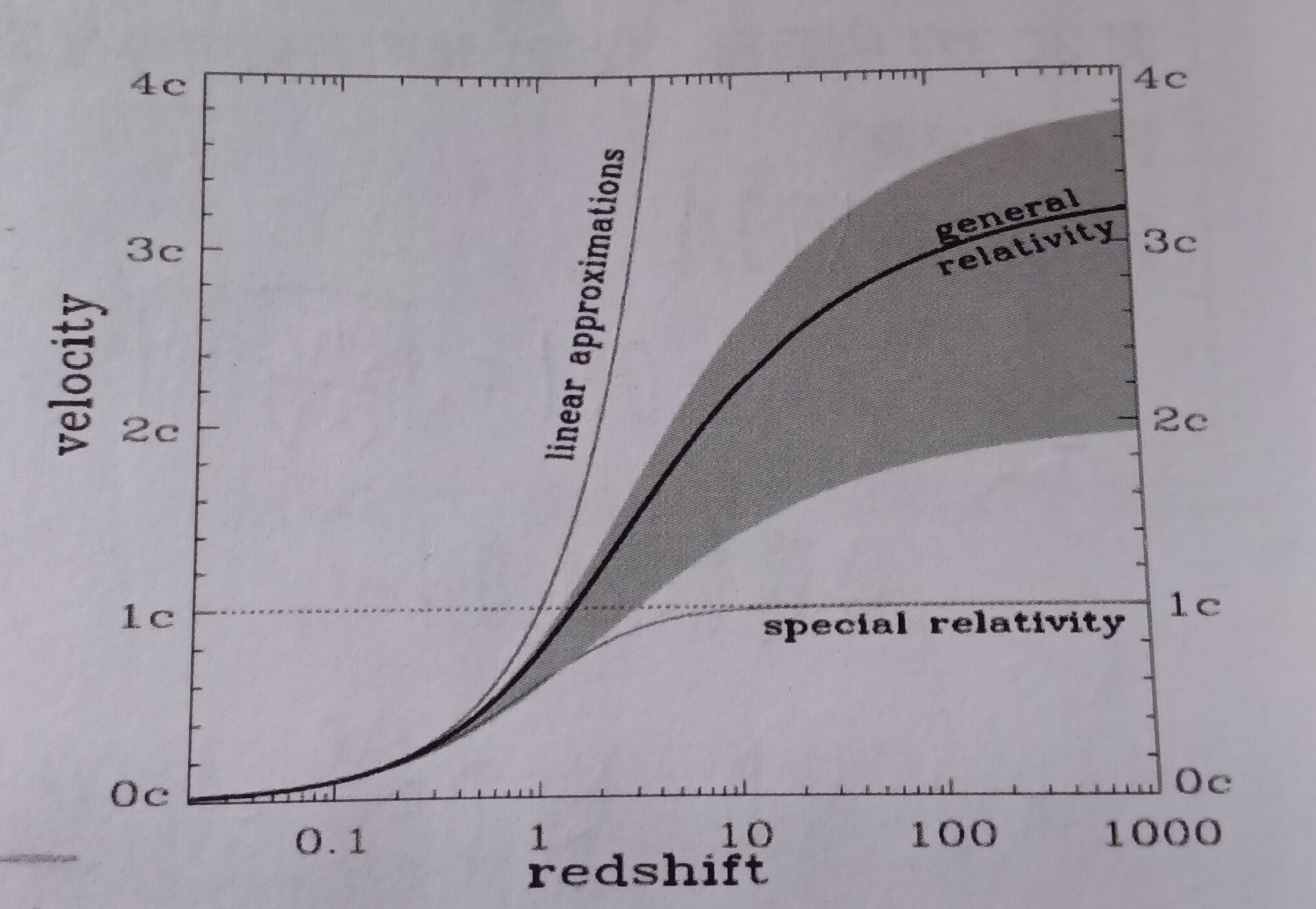
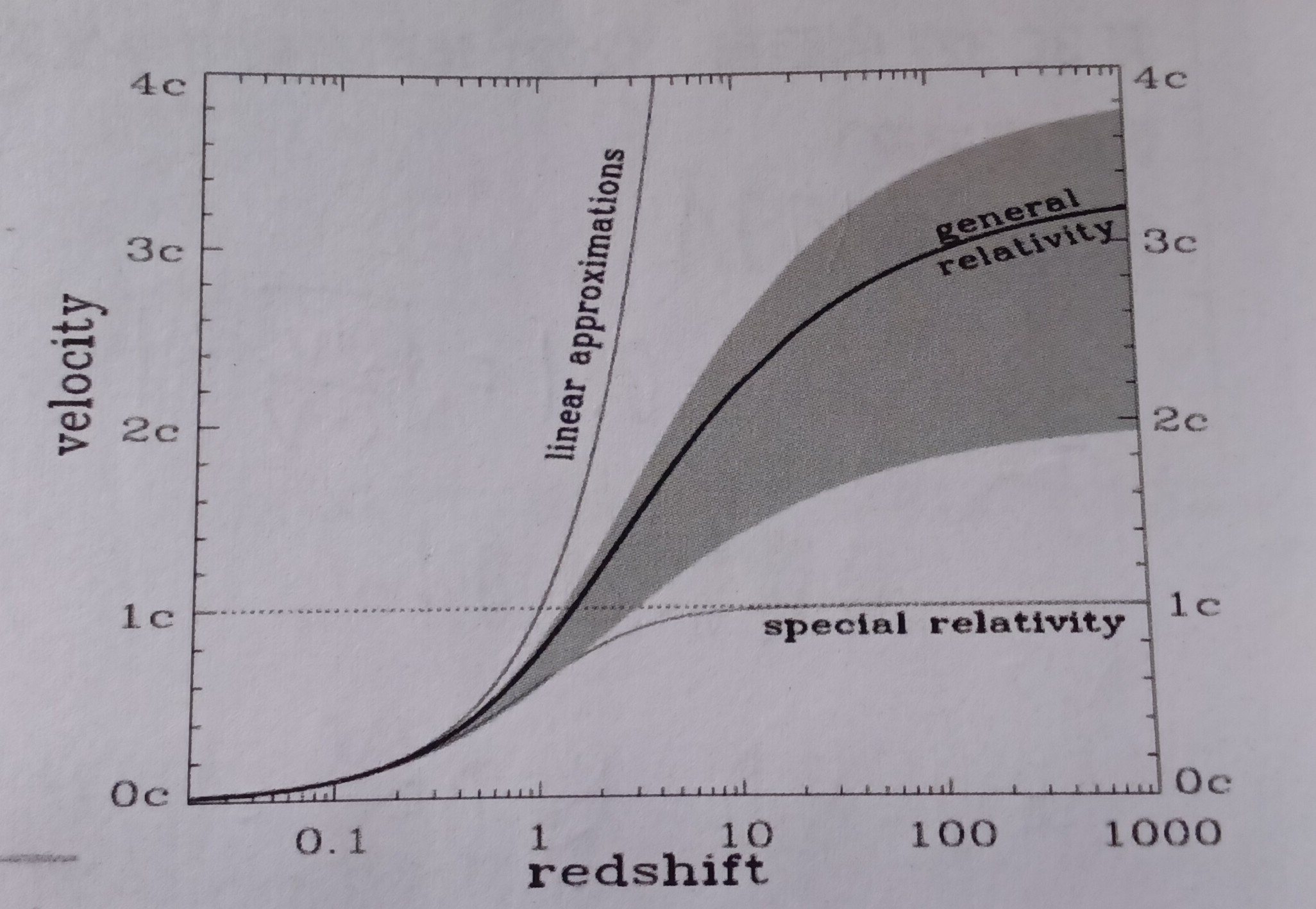
首先需要指出，通过$cz=HD$与狭义相对论修正的$1 + c = \sqrt{\frac{1-\frac{v}{c}}{1+\frac{v}{c}}}$算出的退行速度在红移量大时都是不合理的。前者红移量正比于距离，远远超出实际值；而后者由于宇宙膨胀允许超光速，会导致算出的红移速度永远小于c，低于实际值。下图的general relativity与其所处的灰色区域指当前的推算关系，linear approximations指$cz=HD$的推算关系，special relativity指狭义相对论修正开普勒公式的推算关系。

接下来，我们看看星系年龄与红移量的关系。我们都知道，星系红移量越大年龄越老，这一关系是怎么得出的呢？

我们熟知的哈勃常数，它准确的定义是标度因子$\alpha$的相对变化率：$H = \alpha\frac{d\alpha}{\alpha dt}$

其中$\alpha$的值在当下取1，过去<1，尺度因子$\alpha = \frac{1}{1 + z}$

由于哈勃常数在不同时间取值不同，我们对其做积分得到时间：

$t = \int^z_0 \frac{\alpha}{H(\alpha)} d\alpha$

为了方便使用，我们列出几个数据点（$H_0 = 67.4km/s/Mpc,\omega_m = 0.315,\omega_\Lambda = 0.685, \omega_k = 0$）：

$\begin{array}{|c|c|}z=1&79.6亿年前\\z=2&105.5亿年前\\z=3&115.8亿年前\\z=4&121.6亿年前\\z=5&121.6亿年前\\z=6&127.8亿年前\\z=7&129.6亿年前\end{array}$

通过物理推导，宇宙中辐射组分的能量密度$L \propto (1+z)^4$，如果把宇宙视为黑体，又有$L \propto T^4$，故背景辐射温度$T \propto (1+z)$。