物理 天文竞赛专题----球面几何
O-box,启动!
说明:本帖为天文/地理竞赛帖,其中的球面几何知识可能不太符合物理竞赛要求,不过有科学错误欢迎指出
前文请看普鲁士蓝的天文分享帖的第二章
首先定义恒星位置的几个参数:
赤经α/赤纬δ:恒星在(第二)赤道坐标系下的经纬度。这一坐标系以春分点为δ=0,天赤道为α=0,北极星α=90°,且永远有一条经度线与子午线重合(即北极点永远在地平坐标系正北方向)。因此该坐标系相对地平坐标系是运动的,随着地球的自转而旋转。所有涉及经度的均用0h-24h表示0°-360°。
方位角A/高度角h:恒星在地平坐标系下的经纬度。这一坐标系以南点为A=0,地平面为h=0,北点A=180°,高度角即观察者观察时的仰角。
时角t:恒星在第一赤道坐标系下的经度,该坐标系下纬度为赤纬。该坐标系相对地平坐标系不动,时角相当于一根从北极点指向恒星位置的时针的示数,随恒星东升西落而变化。规定恒星上中天(即地平高度角最大时)t=0h,顺时针增加,下中天时为12h。
恒星时S:通过恒星日计量的时间。规定秋分点恒星时与太阳时重合,此后每天领先太阳时约3m56s,元旦时差约为6h21m。
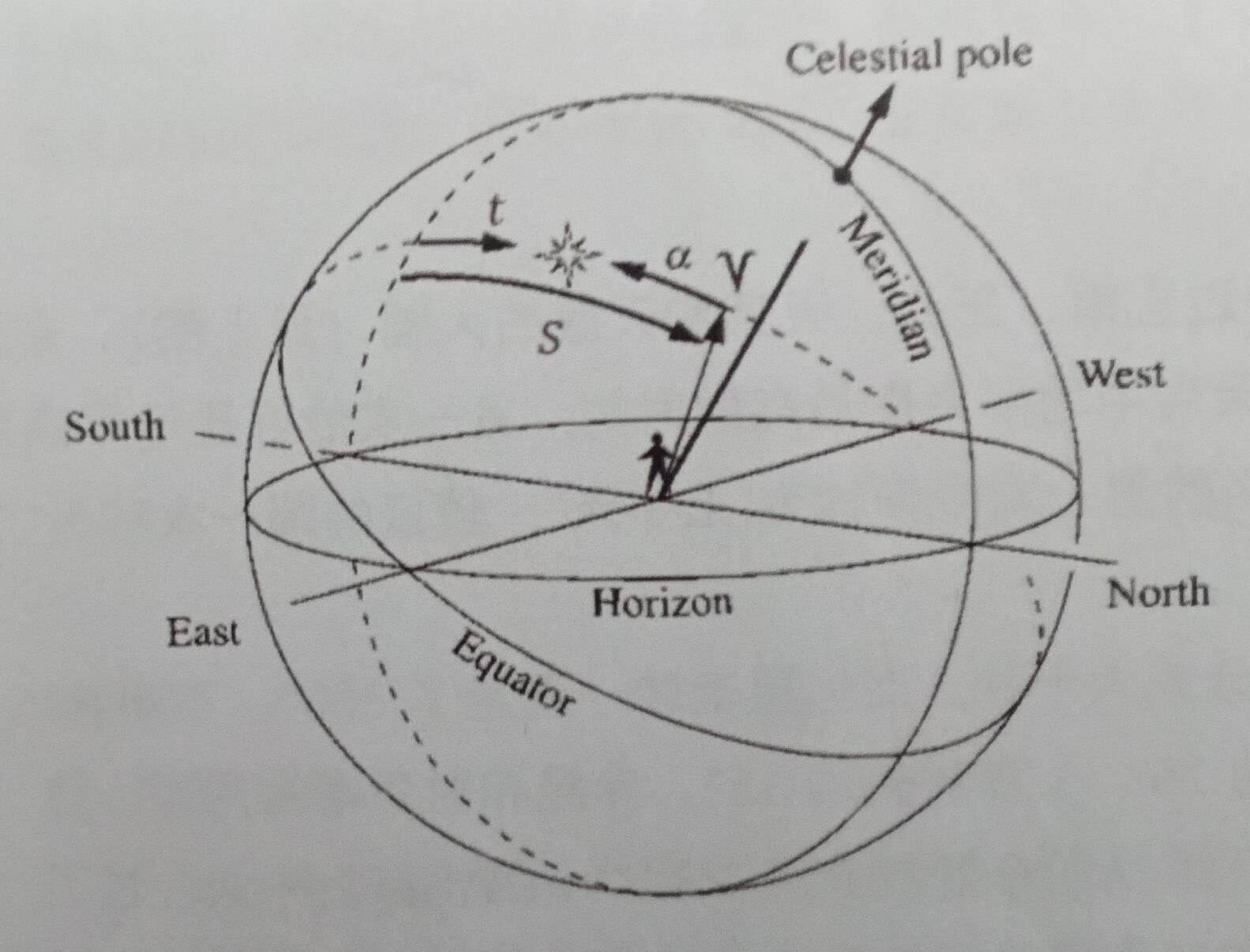
通过以上的介绍,我们描绘一颗恒星与春分点(羊角符号)的升落:
可以看到,球面的大圆上,恒星与春分点的距角即为赤经α,通过南北的子午线表示上中天位置,因此通过上下中天位置的大圆弧上的点与极点的距角即为时角t。我们可以得出:
$\boxed{春分点时角=恒星时}$
接下来,细心的同学已经发现了,恒星的赤经与春分点的赤经之和,恰好等于春分点的时角,因此对所有恒星有:
$\boxed{S=α+t}$
有了这些,我们对整个天球进行建模(以下“弧XX”的角度均指弧的圆心角角度):
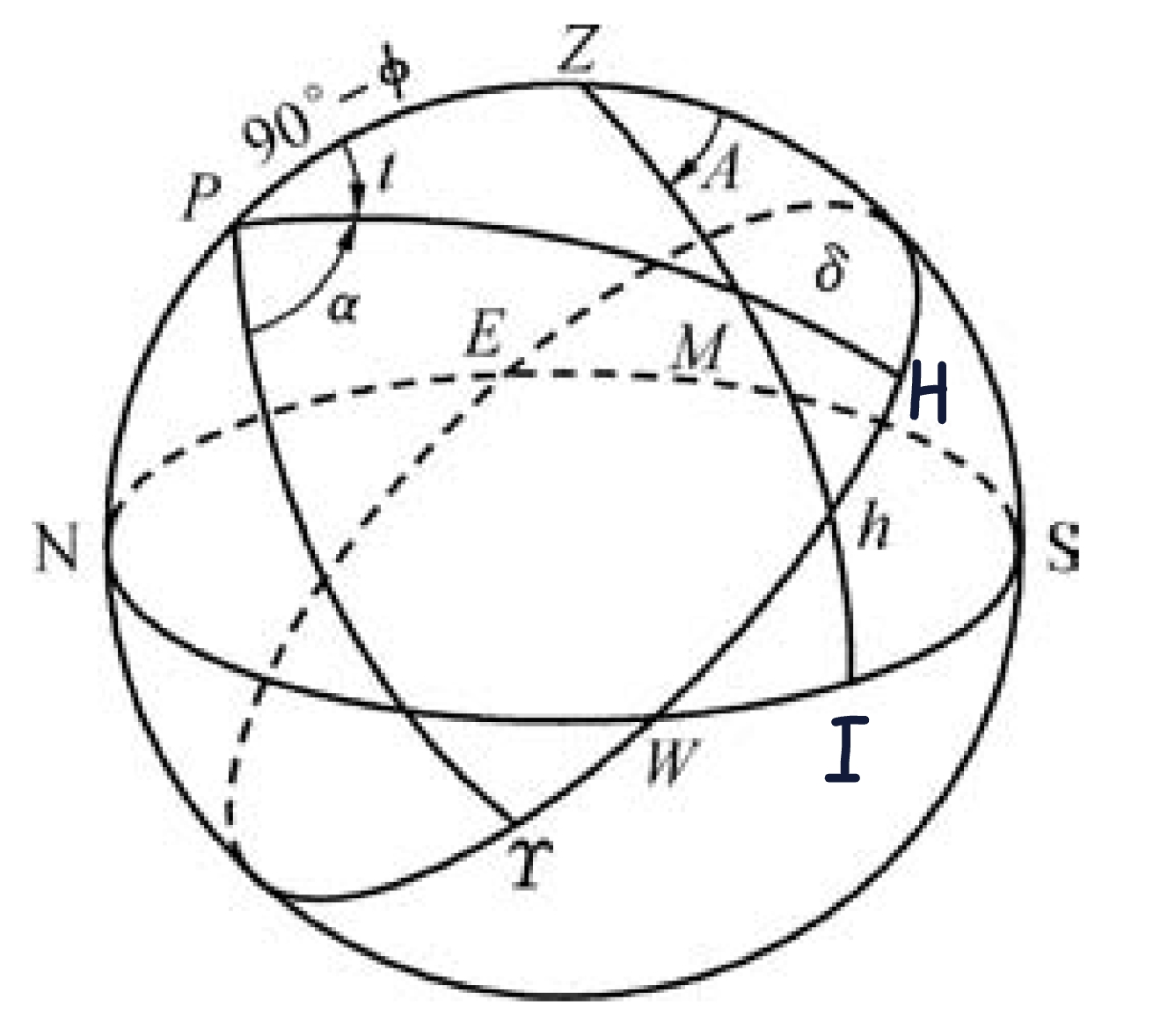
图上M点为恒星,羊角为春分点,倾斜的大圆为天赤道,水平的大圆为地平面。显然北极星高度角等于当地纬度φ。过北极点作弧PM垂直于天赤道交于H,MH即为赤纬δ,YH即为赤经α(为什么弧YH的圆心角等于∠YPH?我们后文会提到)。∠ZPM即为时角t,过天顶Z作弧ZM垂直于地平面交于I,弧SI(等于∠IZS)为方位角A,弧IM为高度角h。
接下来我们搬出球面三角形公式:
$\frac{\sin A}{\sin a} = \frac{\sin B}{\sin b} = \frac{\sin C}{\sin c}$
$\cos c = \cos a\cos b + \sin a\sin b\cos C$
$\cos C = -\cos A\cos B + \sin A\sin B\cos c$
$\sin c\cos B = \cos b\sin a - \sin b\cos a\cos C$
$\sin C\cos b=\cos B\sin A + \sin B\cos A\cos c$
接下来我们在三角形PZM内进行推导:
三角形中,∠PZM=180°-A,∠ZPM=t,PM=90°-δ,PZ=90°-φ,MZ=90°-h。
套用球面三角公式可以得到:
$\sin h = \cos(90°-h) = \sin φ\sinδ + \cos φ\cos δ\cos t$(三角恒等变换略)
$\sin A = \frac{\cos δ\sin t}{\cos h}$
$\cos A = \frac{\sin φ\sin h - \sinδ}{\cos φ\cos h}$
还有一些推导公式:
由公式(1),$\frac{\sin(180°-A)}{\sin (90°-δ)} = \frac{\sin t}{\sin (90°-h)}$,
则有$\sin A\cos h = \sin t\cos δ$
恒星升落时的两个关系:
由公式(3),$\cos (90°-δ) = \cos (90°-φ)\cos (90°-h) - \sin (90°-φ)\sin (90°-h)\cos (180°-A)$
升落时h=0,代入得$\boxed{\cos A = - \frac{\sin δ}{\cos φ}}$
同理得$\boxed{\cos t = - \tan δ\tan φ}$
共4条回复
时间正序