物理 Mentha的循水
我这儿是水贴哦~不是题目互答哦~尤其不要问我物理题哦~我是数竞生我对不起物理![]() 喵酱喵酱~ ^-^^-^♡♡🌿🌿🌿
喵酱喵酱~ ^-^^-^♡♡🌿🌿🌿
放道题稀释一下水量呀,喵酱喵酱~^-^^-^🌿🌿🌿
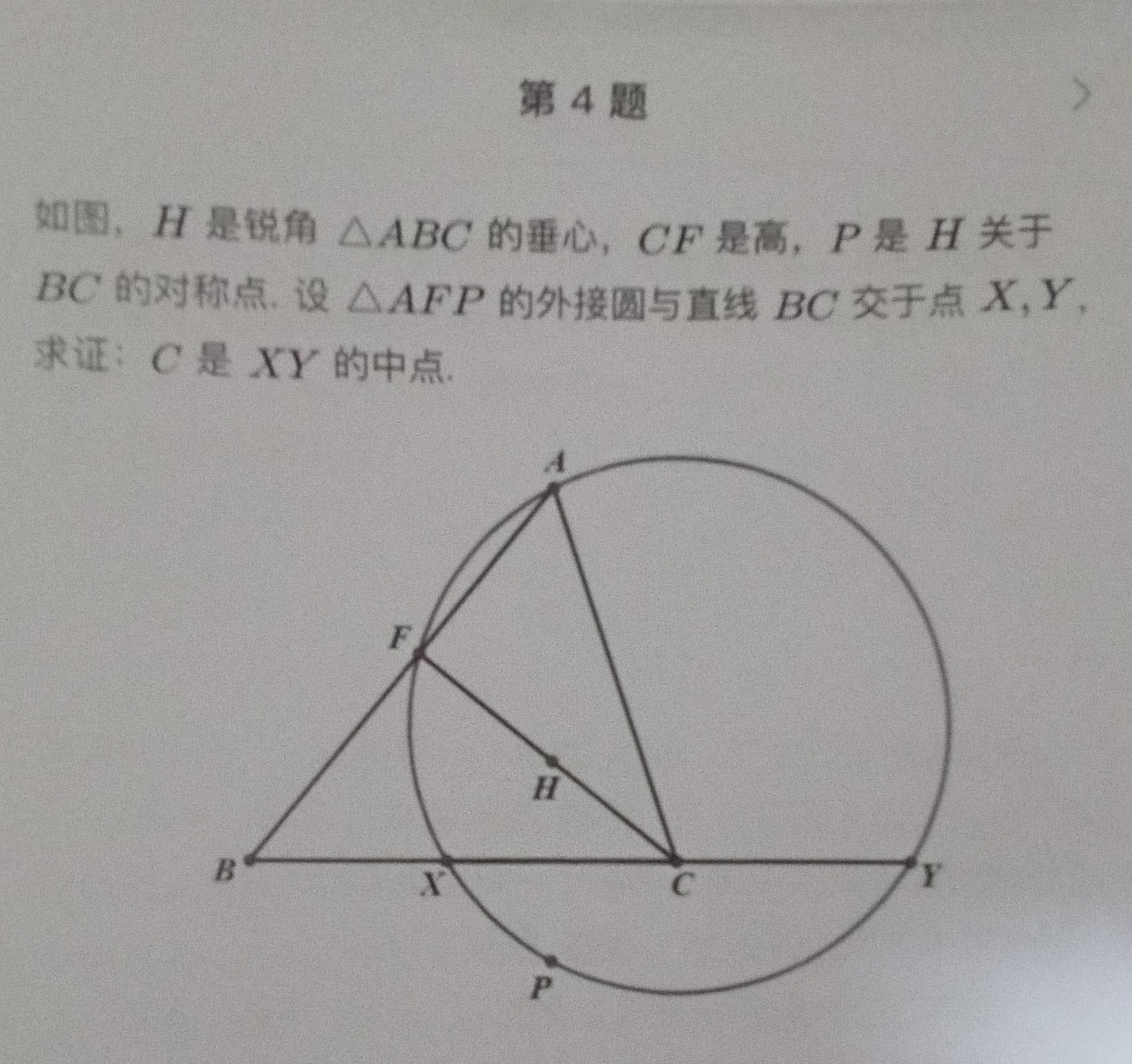
是今年usamo的题,难度还可以吧,反正第一题和第四题特别简单,第四题个人觉得还没有中考几何难,喵酱喵酱~^-^^-^♡🌿🌿🌿


然后是新星赛和东南赛的呢(个人感觉新星的题比东南的好呢





最后是去年cmo的题(这个是真正的大佬!死难!)喵酱喵酱~^-^^-^♡🌿🌿🌿



不保证对哦,因为我这儿题有点多呢,做完就随便丢,现在找可能会搞混呢,有需要可以自取哦~看不清的可以来找我哦~喵酱喵酱~^-^^-^♡♡🌿🌿🌿
这是一个水贴!非常非常水的那种!谢谢 ^-^^-^♡♡🌿🌿🌿
- 时间正序
- 时间倒序
- 评论最多
- 1
哈哈哈,为了督促弟弟学习,我直接把新星赛的题发给你了哈,不用谢我呢,喵酱喵酱~^-^^-^🌿🌿@世界是一个巨大的涨落对吗

这个这个,即答原话♡♡🌿🌿
极限是微积分的基础,它既是导数的基础,也是积分的基础。下面分别解释极限与导数、积分之间的关系。
### 1. 极限与导数
$**导数的定义**直接依赖于极限的概念。具体来说,函数 f(x) 在点 x = a 处的导数 f'(a) 定义为:$
$ f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} $
这里,导数被定义为一个差商的极限。因此,要理解导数,首先需要理解极限的概念。极限帮助我们描述函数在某一点附近的瞬时变化率,而这正是导数的直观意义。
### 2. 极限与积分
$**定积分的定义**也依赖于极限的概念。具体来说,函数 f(x)在区间 [a, b]上的定积分 \int_a^b f(x) dx $可以通过黎曼和的极限来定义。黎曼和的形式为
$S_n = \sum_{i=1}^n f(x_i^*) \Delta x$
$其中\Delta x = \frac{b-a}{n}, x_i^* 是区间[x_{i-1}, x_i]内的任意点。定积分定义为:$
$\int_a^b f(x) dx = \lim_{n \to \infty} S_n$
$即当区间划分越来越细( n \to \infty )时,$黎曼和的极限值就是定积分的值。因此,积分的定义同样基于极限的概念。
### 3. 总结
- **导数** 是通过极限来定义的,描述函数在某一点的瞬时变化率。
- **积分** (特别是定积分)也是通过极限来定义的,描述函数在某个区间上的累积效果。
因此,可以说 **极限是导数和积分共同的基础** 。极限提供了微积分中核心概念的严谨数学表述,使得导数和积分的定义和性质得以严格建立。
$所以,极限既是导数的基础,也是积分的基础。答案是 \boxed{\text{导数和积分}}$